Estimating flow arrivals

Flow arrivals are defined only for TCP flows which should start with one SYN packet. A flow is considered to have arrived in a bin if its SYN packet is in that time bin. Flows active during a certain bin, but with their SYN packet before the bin do not count as flow arrivals for that bin (but they count as active flows). If we look a the core flow slicing algorithm we can use the following estimator to compute the number of flow arrivals.

$$\widehat{a}=\left\{\begin{array}{ll} 1/p & \textrm{if SYN flag set}\\ 0 & \textrm{if SYN flag not set} \end{array}\right.$$ (4)

Given that the SYN flag is set in the flow record if it was set in any of the packets counted against the record, it is trivial to prove that $\widehat{a}$ leads to unbiased estimates of the number of flow arrivals if we make an assumption.

Assumption 1   Only the first packet for the flow can have the SYN flag set.

The flow arrival information is preserved by random packet sampling. Duffield et al. propose two estimators of the number of flow arrivals that work based on flow records collected after random sampling of the traffic [9]. The formulas for the individual contributions of flow records to the total estimate of the number of flow arrivals are as follows.

$$\widehat{M}^{(1)} = \left\{\begin{array}{ll} 1/q & \textrm{if SYN flag set}\\ 0 & \textrm{if SYN flag not set} \end{array}\right.$$

$$\widehat{M}^{(2)} = \left\{\begin{array}{ll} 1/q & \textrm{if SYN flag set and $s=1$}\\ 1 & \textrm{if SYN flag not set or $s>1$}\\ \end{array}\right.$$

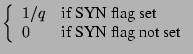Duffield et al. show [9] that both estimators are unbiased $E[\widehat{M}^{(1)}]=E[\widehat{M}^{(2)}]=1$ for flows that have exactly one SYN packet. Both estimators overestimate the number of flow arrivals if flows have more than 1 SYN packet. For flows without any SYN packets which according to our definition of flow arrivals (which differs slightly from that used in [9]) should not be counted, we have $E[\widehat{M}^{(1)}]=0$ and $E[\widehat{M}^{(2)}]>0$, so to make the second estimator unbiased we need another assumption.

Assumption 2   The first packet within the bin for every flow has the SYN flag set.

Flows retaining SYN packets after the random packet sampling stage will retain a single SYN packet, and $\widehat{M}^{(1)}$ estimates the number of flow arrivals based on the number of such flows. We can easily combine it with $\widehat{a}$ to get an estimator for the number of flow arrivals for the combined algorithm using random packet sampling and flow slicing.

$$\widehat{A}^{(1)}=\left\{\begin{array}{ll} 1/(pq) & \textrm{if SYN flag set}\\ 0 & \textrm{if SYN flag not set} \end{array}\right.$$ (5)

$\widehat{M}^{(2)}$ treats separately flows that only have a SYN packet after packet sampling and the others that survive it. Fortunately we can differentiate between the two types of flows even after flow slicing is applied: if a flow with a single SYN packet is sampled by flow slicing its record will have $c_s=1$ and the SYN flag set; if any other flow is sampled by flow slicing and it has $c_s=1$ at the end of the bin it means that only its last packet was sampled thus it will not have the SYN flag set because that would put it into the category of flows with a single SYN packet surviving the packet sampling. Thus we can combine $\widehat{M}^{(2)}$ with $\widehat{a}$ to obtain another estimator.

$$\widehat{A}^{(2)}=\left\{\begin{array}{ll} 1/(pq) & \textrm{if SY... ...nd $c_s=1$}\\ 1 & \textrm{if SYN flag not set and $c_s>1$}\\ \end{array}\right.$$ (6)

Note that if assumption 1 is violated and we have more than one SYN packet at the beginning of the flow, say due to SYN retransmissions, both estimators will be biased towards over-counting. But if repeated SYNs are a rare enough occurrence, the effect on a final estimate based on many flow records will be small.