Next: Differential Frequency Error and Up: Background Previous: Frequency, Resolution, and Power

| Device | Granularity | Stability | Power |
| Tuning Fork XO | Coarse | 100ppm | |
| Fox F254 32k Osc | Coarse | 100ppm | |
| AT-Cut Quartz XO | Fine | 25ppm | |
| DS32KHz 32K TCXO | Coarse | 7.5ppm | |
| DS3232 32KHz TCXO | Coarse | 2ppm | |
| DS4026 10MHz TCXO | Fine | 1ppm | |
| ACHL 10MHz Osc | Fine | 30ppm | |
| Crystek C3392 10MHz | Fine | 30ppm | |
| 8MHz XCXT | Fine | 1ppm | |
| Smart Timer Unit | Fine | 1ppm |
|
Assume that the frequency of a clock as a function of temperature is denoted by the function ![]() .
Its nominal frequency is designated as
.
Its nominal frequency is designated as ![]() , and thus the frequency error is
, and thus the frequency error is
![]() . The normalized frequency error is calculated as
. The normalized frequency error is calculated as
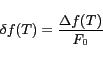
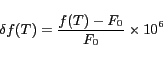
Thermal variation is the single most significant contributor to clock frequency error. Thus, changes in the ambient temperature are reflected in the frequency of a node's clock. The most common way to counterbalance this effect in quartz-crystal based oscillators is to measure the temperature and adjust the crystal oscillator (by changing its load capacitance) using a set of predetermined corrections. Commercial Temperature Compensated Crystal Oscillators (TCXO) embody this approach, but adding thermal measurement and analysis logic not only increases the production cost, but power consumption as well. TCXO's are often unfeasible for the strict low power requirements of WSN's. In Table 1, a representative set of oscillators (including several TCXO's) are compared in terms of stability and power.
Thomas Schmid 2008-11-14