
One of the most challenging facets of the botnet membership problem lies in discerning the relationship among (seemingly) different botnets. To highlight this, we examine the existence of hidden relations among the botnets we tracked. The presence of these relations raises new challenges to the accuracy of botnet population counting techniques. Specifically, for botnets that are related, is the aggregate population count simply the sum of the different botnet populations? Or more importantly, how do we characterize the overlap between different botnet populations? In what follows, we discuss our methodology for finding potential hidden relationships among botnets.
# <DNS name> <Channel> <Server ID> <Botmaster ID> <Server Version>
[1] hid.shgon.net #!GT!# IRC.Death.TeaM.KW [Lindi_Cracker]-1!HackPimp Unreal3.2.5
[2] bruimi.shgon.net #!GT!# IRC.Death.TeaM.KW ChanServ!Coder Unreal3.2.5
[3] newbot.shgon.net #.rxb0t IRC.Death.TeaM.KW Chan!Coder Unreal3.2.5
[4] bb.shgon.net #.rxbot IRC.Death.TeaM.KW Chan!Coder Unreal3.2.5
|
First, we create for each botnet a ![]() -dimensional structural feature
vector
-dimensional structural feature
vector
![]() . We choose the following
features to represent a botnet's unique identity:
. We choose the following
features to represent a botnet's unique identity:
To reveal the existence of clusters of related botnets we then create a
proximity matrix ![]() by calculating a pair-wise scores across
all botnet vectors,
by calculating a pair-wise scores across
all botnet vectors,
![]() . For a pair of vectors
. For a pair of vectors
![]() the pair-wise score
the pair-wise score ![]() is a weighted dot
product of the two vectors.
is a weighted dot
product of the two vectors.
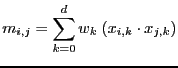 |
where ![]() is the weight assigned to dimension
is the weight assigned to dimension ![]() and the
product of the two vector fields is one if they are identical, or zero
otherwise. Considering that similarity in the names of the IRC servers
implies strong correlation between two botnets, we assign a weight of
1.5 to the IRC server dimension, while all other dimensions are given
equal weights of 0.5.
and the
product of the two vector fields is one if they are identical, or zero
otherwise. Considering that similarity in the names of the IRC servers
implies strong correlation between two botnets, we assign a weight of
1.5 to the IRC server dimension, while all other dimensions are given
equal weights of 0.5.
Given the matrix ![]() , we infer related botnets by extracting
botnet groups that have pairwise similarity scores above a threshold
, we infer related botnets by extracting
botnet groups that have pairwise similarity scores above a threshold
![]() . We choose
. We choose
![]() , so that two botnets are related if
they have the same IRC server DNS name or match in at least three
other dimensions.
, so that two botnets are related if
they have the same IRC server DNS name or match in at least three
other dimensions.