Next: End-to-End Support Up: IO Resource Management Previous: Analogy to TCP

The PARDA algorithm detects overload at the array based on average IO latency measured over a fixed time period, and adjusts the host's issue queue length (i.e., window size) in response. A separate instance of the PARDA control algorithm executes on each host.
There are two main components: latency estimation and window
size computation. For latency estimation, each host maintains an
exponentially-weighted moving average of IO latency at time ![]() , denoted by
, denoted by ![]() ,
to smooth out short-term variations. The weight given to past
values is determined by a smoothing parameter
,
to smooth out short-term variations. The weight given to past
values is determined by a smoothing parameter
![]() . Given a new latency observation
. Given a new latency observation ![]() ,
,
| (1) |
The window size computation uses a control mechanism
shown to exhibit stable behavior for FAST TCP:
Whenever the average latency
![]() , PARDA decreases the window
size. When the overload subsides and
, PARDA decreases the window
size. When the overload subsides and
![]() , PARDA increases
the window size. Window size adjustments are based on latency
measurements, which indicate load at the array, as well as per-host
, PARDA increases
the window size. Window size adjustments are based on latency
measurements, which indicate load at the array, as well as per-host
![]() values, which specify relative host IO share allocations.
values, which specify relative host IO share allocations.
To avoid extreme behavior from the control algorithm, ![]() is
bounded by
is
bounded by
![]() . The lower bound
. The lower bound ![]() prevents
starvation for hosts with very few IO shares. The upper bound
prevents
starvation for hosts with very few IO shares. The upper bound
![]() avoids very long queues at the array, limiting the latency
seen by hosts
that start issuing requests after a period of inactivity. A
reasonable upper bound can be based on typical queue length values in
uncontrolled systems,
as well as the array
configuration and number of hosts.
avoids very long queues at the array, limiting the latency
seen by hosts
that start issuing requests after a period of inactivity. A
reasonable upper bound can be based on typical queue length values in
uncontrolled systems,
as well as the array
configuration and number of hosts.
The latency threshold ![]() corresponds to the response time that
is considered acceptable in the system, and the control algorithm
tries to maintain the overall cluster-wide latency close to this
value.
Testing confirmed our expectation that increasing the array queue
length beyond a certain value doesn't lead to increased throughput.
Thus,
corresponds to the response time that
is considered acceptable in the system, and the control algorithm
tries to maintain the overall cluster-wide latency close to this
value.
Testing confirmed our expectation that increasing the array queue
length beyond a certain value doesn't lead to increased throughput.
Thus, ![]() can be set to a value which is high enough
to ensure that a
sufficiently large number of requests can always be pending at the
array. We are also exploring automatic techniques for setting this
parameter based on long-term observations of latency and throughput.
Administrators may alternatively specify
can be set to a value which is high enough
to ensure that a
sufficiently large number of requests can always be pending at the
array. We are also exploring automatic techniques for setting this
parameter based on long-term observations of latency and throughput.
Administrators may alternatively specify ![]() explicitly, based
on cluster-wide requirements, such as supporting
latency-sensitive applications, perhaps at the cost of under-utilizing the
array in some cases.
explicitly, based
on cluster-wide requirements, such as supporting
latency-sensitive applications, perhaps at the cost of under-utilizing the
array in some cases.
|
Finally, ![]() is set based on the IO shares associated with the
host, proportional to the sum of its per-VM shares. It has been shown
theoretically in the context of FAST TCP that the equilibrium window
size value for different hosts will be proportional to their
is set based on the IO shares associated with the
host, proportional to the sum of its per-VM shares. It has been shown
theoretically in the context of FAST TCP that the equilibrium window
size value for different hosts will be proportional to their ![]() parameters [15].
parameters [15].
We highlight two properties of the control equation, again relying on
formal models and proofs from FAST TCP. First, at
equilibrium, the throughput of host ![]() is proportional to
is proportional to
![]() , where
, where ![]() is the per-host allocation parameter,
and
is the per-host allocation parameter,
and ![]() is the queuing delay observed by the host. Second,
for a single array with capacity
is the queuing delay observed by the host. Second,
for a single array with capacity ![]() and latency threshold
and latency threshold
![]() , the window size at equilibrium will be:
, the window size at equilibrium will be:
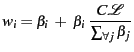 |
(3) |
To illustrate the behavior of the control algorithm, we simulated a
simple distributed system consisting of a single array and multiple
hosts using Yacsim [17]. Each host runs an instance of the
algorithm in a distributed manner, and the array services requests
with latency based on an exponential distribution with a mean of
![]() . We conducted a series of experiments with various capacities,
workloads, and parameter values.
. We conducted a series of experiments with various capacities,
workloads, and parameter values.
To test the algorithm's adaptability, we experimented with three hosts
using a ![]() share ratio,
share ratio, ![]() = 200 ms, and an array capacity
that changes from 400 req/s to 100 req/s halfway through the
experiment. Figure 2 plots the throughput, window
size and average latency observed by the hosts for a period of
= 200 ms, and an array capacity
that changes from 400 req/s to 100 req/s halfway through the
experiment. Figure 2 plots the throughput, window
size and average latency observed by the hosts for a period of ![]() seconds. As expected, the control algorithm drives the system to
operate close to the desired latency threshold
seconds. As expected, the control algorithm drives the system to
operate close to the desired latency threshold ![]() . We also used
the simulator to verify that as
. We also used
the simulator to verify that as ![]() is varied (100 ms, 200 ms
and 300 ms), the system latencies operate close to
is varied (100 ms, 200 ms
and 300 ms), the system latencies operate close to ![]() , and that
windows sizes increase while maintaining their proportional ratio.
, and that
windows sizes increase while maintaining their proportional ratio.
Ajay Gulati 2009-01-14