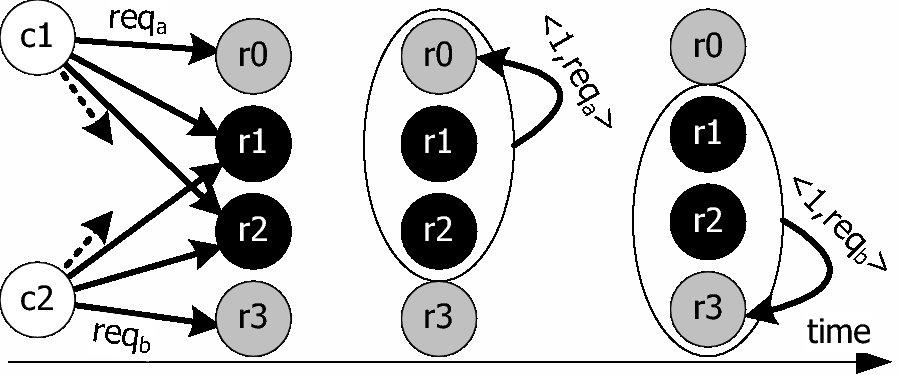
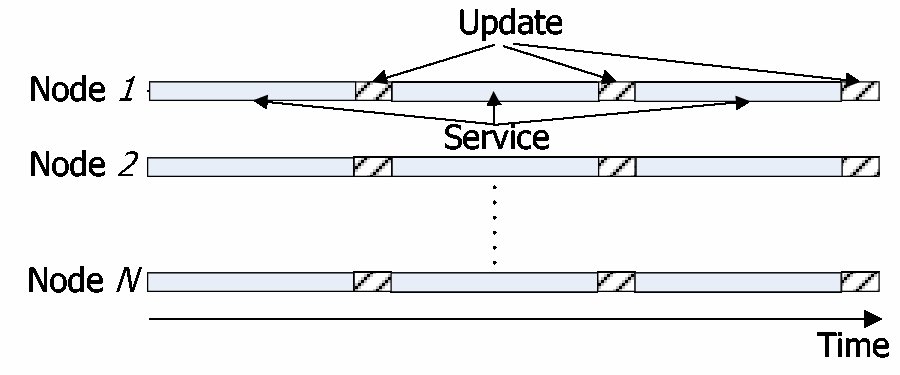
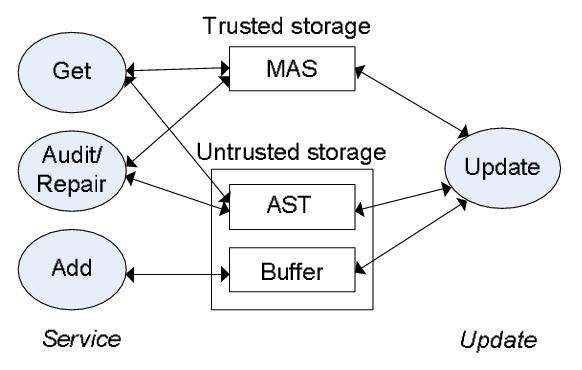
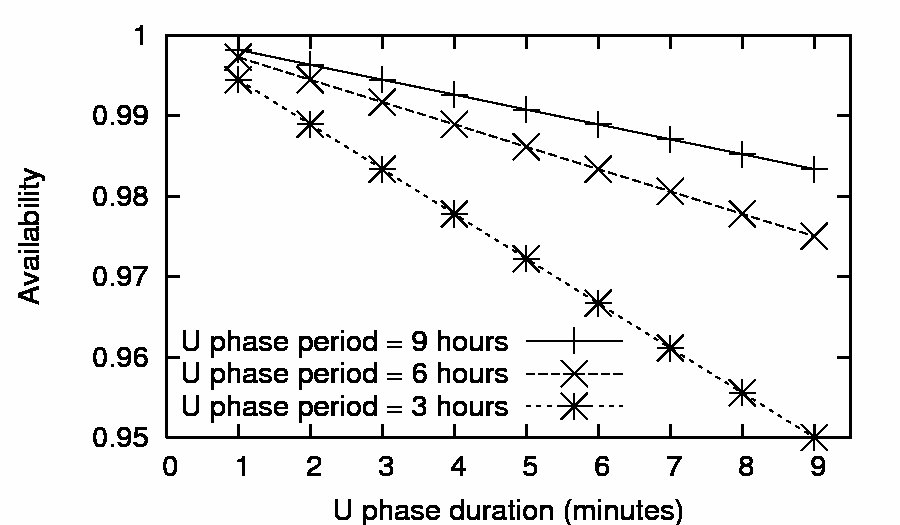
| Client.Get(key) |
|
// quo_RPC sends msg to R, collects matching responses on non-* |
// fields from a quorum of given size, retransmits on timeout |
| ⟨ Reply, *, value, witness, * ⟩ ← quo_RPC(⟨Get, key⟩, f+1) |
| return value |
| Server.Get(client, key)i // this is server i |
|
⟨ value, witness ⟩ ← lookup_AST(key) |
|
att ← lookup_MAS(qs) // attestation |
|
send client a ⟨ Reply, i, value, witness, att ⟩ |
|
| Client.Add(key,value) |
|
⟨ TentReply, *, key, value⟩ ← |
|
quo_RPC(⟨Add, key, value⟩, 2f+1) |
|
// at this point, the client holds a tentative reply |
|
collect Reply messages // in the next S phase |
|
if (f+1 valid, matching replies are collected) |
|
return accepted(key, value) |
| Server.Add(client, key, value)i |
|
if (⟨ key, value'⟩ in AST), treat as a Get and return |
|
add ⟨ client, key, value ⟩ to Adds |
|
send client a ⟨ TentReply, i, key, value⟩ |
|
| Server.Audit(ASTNode,hASTNode)i |
|
status ← check ASTNode,hASTNode |
|
if (status invalid) repair ASTNode // fetch from other |
|
for each child C of ASTNode |
|
Audit(C, hC) // hC is contained in the label of ASTNode |
|
| Server.Start_Service(Committed_Adds)i |
|
// reply for Adds committed in the previous U phase |
|
for each ⟨ key, value, client ⟩ in Committed_Adds |
|
send client a ⟨ Reply, i, value, witness, att ⟩ |
Figure 4: Simplified service process pseudocode.