


Next: Inverted Tree-like Hierarchy
Up: More Complex Cache Hierarchies
Previous: More Complex Cache Hierarchies
We use a hierarchy of three caches, 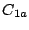 (
(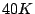 blocks) and
blocks) and 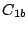 (
(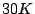 blocks) at the first level, and a shared cache
blocks) at the first level, and a shared cache 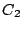 (
(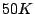 blocks) at the second-level (see Figure 14). While
blocks) at the second-level (see Figure 14). While 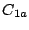 serves one of P2, P3, P4 or P5 traces,
serves one of P2, P3, P4 or P5 traces, 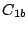 serves the P1 trace.
We impose no bandwidth restrictions and assume free demotions for the DEMOTE algorithm.
We observe that for all four combinations, the PROMOTE-LRU has equal or better average response time while generating only half the inter-cache traffic than
DEMOTE-LRU. DEMOTE cannot be applied to tree-like ARC hierarchies, allowing
PROMOTE-ARC to win by default. This is because DEMOTE simulates a global ARC algorithm which adapts the ratio of the global ARC lists,
serves the P1 trace.
We impose no bandwidth restrictions and assume free demotions for the DEMOTE algorithm.
We observe that for all four combinations, the PROMOTE-LRU has equal or better average response time while generating only half the inter-cache traffic than
DEMOTE-LRU. DEMOTE cannot be applied to tree-like ARC hierarchies, allowing
PROMOTE-ARC to win by default. This is because DEMOTE simulates a global ARC algorithm which adapts the ratio of the global ARC lists, 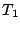 and
and
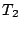 . In single-path scenarios, the same ratio of the two ARC lists,
. In single-path scenarios, the same ratio of the two ARC lists,
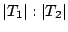 , can be enforced at all levels. However, in multi-path scenarios, this is not always possible, as the amount of
, can be enforced at all levels. However, in multi-path scenarios, this is not always possible, as the amount of 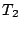 pages in a cache depends on the workload it sees, and the ratio determined by ARC may not be enforceable.
pages in a cache depends on the workload it sees, and the ratio determined by ARC may not be enforceable.
In Figure 14, we also show the steps used to compute OPT-UB and OPT-LB in accordance to Section II-D. As usual, we observe that OPT-LB and OPT-UB provide close bounds (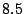 % apart) on the optimal performance for the given hierarchy.
% apart) on the optimal performance for the given hierarchy.


Next: Inverted Tree-like Hierarchy
Up: More Complex Cache Hierarchies
Previous: More Complex Cache Hierarchies
root
2008-01-08

![]() % apart) on the optimal performance for the given hierarchy.
% apart) on the optimal performance for the given hierarchy.