
An Analysis of Data Corruption in the Storage Stack
Abstract:
An important threat to reliable storage of data is silent
data corruption. In order to develop suitable protection mechanisms
against data corruption, it is essential to understand its characteristics.
In this paper, we present the first large-scale study of
data corruption. We analyze corruption instances recorded in
production storage systems containing a total of 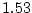 million disk drives,
over a period of
million disk drives,
over a period of 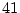 months. We study three
classes of corruption: checksum mismatches, identity discrepancies, and parity inconsistencies.
We focus on checksum mismatches since they occur the most.
months. We study three
classes of corruption: checksum mismatches, identity discrepancies, and parity inconsistencies.
We focus on checksum mismatches since they occur the most.
We find more than 400,000 instances of
checksum mismatches over the 41-month period. We find many interesting trends among
these instances including:
(i) nearline disks (and their adapters) develop checksum mismatches an order of magnitude
more often than enterprise class disk drives,
(ii) checksum mismatches within the same disk are not independent events and
they show high spatial and temporal locality, and
(iii) checksum mismatches across different disks in the same storage system are not
independent.
We use our observations to derive lessons for corruption-proof
system design.
1 Introduction
One of the biggest challenges in designing storage systems is
providing the reliability and availability that users expect. Once
their data is stored, users expect it to be persistent forever, and
perpetually available. Unfortunately, in practice there are a number
of problems that, if not dealt with, can cause data loss in storage
systems.
One primary cause of data loss is disk drive unreliability [16].
It is well-known that hard drives are mechanical, moving devices that
can suffer from mechanical problems leading to drive failure and data
loss. For example, media imperfections, and loose particles causing
scratches, contribute to media errors,
referred to as latent sector errors, within disk
drives [18]. Latent sector errors are detected by
a drive's internal error-correcting codes (ECC) and are reported to
the storage system.
Less well-known, however, is that current hard drives and controllers
consist of hundreds-of-thousands of lines of low-level firmware code.
This firmware code, along with higher-level system software, has the
potential for harboring bugs that can cause
a more insidious type of disk error - silent data corruption, where
the data is silently corrupted with no indication from the drive that
an error has occurred.
Silent data corruptions could lead to data loss more often than latent sector errors,
since, unlike latent sector errors, they cannot be detected or repaired by the disk
drive itself.
Detecting and recovering from data
corruption requires protection techniques beyond those provided by the
disk drive.
In fact, basic protection schemes such as RAID [13]
may also be unable to detect these problems.
The most common technique used in storage systems to detect data corruption
is for the storage system to add its own higher-level checksum for each
disk block, which is validated on each disk block read.
There is a long history of enterprise-class storage systems, including
ours, in using checksums in a variety of manners to detect data
corruption [3,6,8,22].
However, as we discuss later, checksums do not protect against all
forms of corruption.
Therefore, in addition to checksums, our storage system also uses file
system-level disk block identity information to detect previously undetectable
corruptions.
In order to further improve on techniques to handle corruption,
we need to develop a thorough understanding of data corruption characteristics.
While recent studies provide information on whole disk
failures [11,14,16] and latent sector errors [2]
that can aid system designers in handling these error conditions, very little is known
about data corruption, its prevalence and its characteristics. This
paper presents a large-scale study of silent data corruption based on
field data from 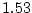 million disk drives covering a time period of
million disk drives covering a time period of 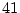 months. We
use the same data set as the one used
in recent studies of latent sector errors [2] and disk failures [11].
We identify the fraction of disks that develop corruption, examine factors that might
affect the prevalence of corruption, such as disk class and age, and
study characteristics of corruption, such as spatial and temporal locality.
To the best of our knowledge, this is the first study of
silent data corruption in production and development systems.
months. We
use the same data set as the one used
in recent studies of latent sector errors [2] and disk failures [11].
We identify the fraction of disks that develop corruption, examine factors that might
affect the prevalence of corruption, such as disk class and age, and
study characteristics of corruption, such as spatial and temporal locality.
To the best of our knowledge, this is the first study of
silent data corruption in production and development systems.
We classify data corruption into three categories based on how it is discovered:
checksum mismatches, identity discrepancies, and parity inconsistencies(described in detail in Section 2.3).
We focus on checksum mismatches since they are found to occur the most.
Our important observations include the following:
(i) During the 41-month time period, we observe more than 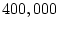 instances of checksum mismatches,
instances of checksum mismatches, 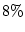 of which were discovered
during RAID reconstruction, creating the possibility of real data
loss. Even though the rate of corruption is small, the discovery
of checksum mismatches during reconstruction illustrates that data
corruption is a real problem that needs to be taken into account by storage system
designers.
of which were discovered
during RAID reconstruction, creating the possibility of real data
loss. Even though the rate of corruption is small, the discovery
of checksum mismatches during reconstruction illustrates that data
corruption is a real problem that needs to be taken into account by storage system
designers.
(ii) We find that nearline (SATA) disks and their adapters develop
checksum mismatches an order of magnitude more often than enterprise class (FC) disks. Surprisingly,
enterprise class disks with checksum mismatches develop more of them than nearline disks with mismatches.
(iii) Checksum mismatches are not independent occurrences - both within a disk and within
different disks in the same storage system.
(iv) Checksum mismatches have tremendous spatial locality;
on disks with multiple mismatches, it is often consecutive blocks that are affected.
(v) Identity discrepancies and parity inconsistencies do occur, but affect 3 to 10 times fewer disks than
checksum mismatches affect.
The rest of the paper is structured as follows.
Section 2 presents the overall architecture of the
storage systems used for the study and Section 3 discusses the methodology used.
Section 4 presents the results of our analysis of
checksum mismatches, and Section 5 presents the results for identity discrepancies, and
parity inconsistencies. Section 6 provides an anecdotal discussion
of corruption, developing insights for corruption-proof storage system
design. Section 7 presents related work and
Section 8 provides a summary of the paper.
2 Storage System Architecture
The data we analyze is from tens-of-thousands of production and development
Network Appliance storage systems
(henceforth called the system) installed at hundreds of customer sites. This
section describes the architecture of the system, its corruption detection mechanisms,
and the classes of corruptions in our study.
storage systems
(henceforth called the system) installed at hundreds of customer sites. This
section describes the architecture of the system, its corruption detection mechanisms,
and the classes of corruptions in our study.
Physically, the system is composed of a storage-controller that
contains the CPU, memory, network interfaces, and storage adapters.
The storage-controller is connected to a set of disk shelves via Fibre
Channel loops.
The disk shelves house individual disk drives. The disks may either
be enterprise class FC disk drives or nearline serial ATA (SATA)
disks. Nearline drives use hardware adapters to convert the SATA
interface to the Fibre Channel protocol. Thus, the storage-controller views all drives as being Fibre Channel (however, for the purposes of the study,
we can still identify whether a drive is SATA and FC using its model type).
The software stack on the storage-controller is
composed of the WAFL
 file system, RAID, and storage layers.
The file system processes client requests by issuing read and write
operations to the RAID layer, which transforms the file system requests into logical disk
block requests and issues them to the storage layer.
The RAID layer also generates parity for writes and reconstructs data after
failures.
The storage layer is a set of customized device drivers that communicate
with physical disks using the SCSI command set [23].
file system, RAID, and storage layers.
The file system processes client requests by issuing read and write
operations to the RAID layer, which transforms the file system requests into logical disk
block requests and issues them to the storage layer.
The RAID layer also generates parity for writes and reconstructs data after
failures.
The storage layer is a set of customized device drivers that communicate
with physical disks using the SCSI command set [23].
Table 1:
Corruption classes summary.
| Corruption Class |
Possible Causes |
Detection Mechanism |
Detection Operation |
| Checksum mismatch |
Bit-level corruption; torn write; misdirected write |
RAID block checksum |
Any disk read |
| Identity discrepancy |
Lost or misdirected write |
File system-level block identity |
File system read |
| Parity inconsistency |
Memory corruption; lost write; bad parity calculation |
RAID parity mismatch |
Data scrub |
|
The system, like other commercial storage systems, is
designed to handle a wide range of disk-related errors. The data
integrity checks in place are designed to detect and recover from
corruption errors so that they are not propagated to the user.
The system does not knowingly propagate corrupt data to the user
under any circumstance.
We focus on techniques used to detect silent data corruption,
that is, corruptions not detected by the disk drive
or any other hardware component. Therefore, we
do not describe techniques used for other errors, such as
transport corruptions reported as SCSI transport errors or
latent sector errors. Latent sector errors are caused by physical problems within the disk drive
such as media scratches, ``high-fly'' writes, etc. [2,18],
and detected by the disk drive itself by its inability to
read or write sectors, or through its error-correction codes (ECC).
In order to detect silent data corruptions, the system stores extra
information to disk blocks. It also periodically reads all disk blocks to
perform data integrity checks. We now describe these techniques in detail.
In order to detect disk block corruptions, the system writes
a 64-byte data integrity segment along with each disk block.
Figure 1 shows two techniques for storing this
extra information, and also describes its structure.
For enterprise class disks, the system uses 520-byte sectors. Thus, a 4-KB file system block is
stored along with 64 bytes of data integrity segment in eight 520-byte sectors. For
nearline disks, the system uses the default 512-byte sectors and store the
data integrity segment for each set of eight sectors in the following sector. We
find that the protection offered by the data integrity segment is well-worth the extra
space needed to store them.
One component of the data integrity segment is a checksum of the entire 4 KB file system block.
The checksum is validated by the RAID layer whenever
the data is read. Once a corruption has been detected, the
original block can usually be restored through RAID reconstruction. We
refer to corruptions detected by RAID-level checksum validation as
checksum mismatches.
A second component of the data integrity segment is block identity information.
In this case, the fact that the file system is part of the storage system
is utilized. The identity is the disk block's identity within the file system
(e.g., this block belongs to inode 5 at offset 100).
This identity is cross-checked at file read time to ensure that the block being
read belongs to the file being accessed. If, on file read, the
identity does not match, the data is reconstructed from parity.
We refer to corruptions that are not detected by checksums, but detected
through file system identity validation as identity discrepancies.
In order to pro-actively detect errors, the RAID layer periodically
scrubs all disks. A data scrub issues read operations for each
physical disk block, computes a checksum over its data, and compares the computed checksum
to the checksum located in its data integrity segment.
If the checksum comparison fails (i.e., a checksum mismatch), the data is reconstructed from other disks
in the RAID group, after those checksums are also verified.
If no reconstruction is necessary, the parity of the data blocks is generated and
compared with the parity stored in the parity block. If the parity
does not match the verified data, the scrub process fixes the parity
by regenerating it from the data blocks.
In a system protected by double parity, it is possible to definitively
tell which of the parity or data block is corrupt.
We refer to these cases of mismatch between data and parity as parity inconsistencies.
Note that data scrubs are unable to validate the extra file system
identity information stored in the data integrity segment, since, by its
nature, this information only has meaning to the file system and not the RAID-level scrub.
Depending on system load, data scrubs are initiated on Sunday
evenings. From our data, we find that an entire RAID group is
scrubbed approximately once every two weeks on an average. However,
we cannot ascertain from the data that every disk in the study
has been scrubbed.
2.3 Corruption Classes
This study focuses on disk block corruptions caused by both hardware and
software errors. Hardware bugs include bugs in the disk drive or the
disk shelf firmware, bad memory, and adapter failures. Software bugs
could also cause some corruption. In many cases, the cause of
corruption cannot be identified.
We detect different forms of corruption using the different data
protection mechanisms in place. As mentioned earlier, we distinguish between these forms in
our study. Table 1 gives a summary of these
corruption classes.
 Checksum mismatches (CMs): This corruption class refers to cases where the
corruption is detected from mismatched data and checksum. The cause
could be
(i) data content corrupted by components within the data path,
or (ii) a torn write, wherein only a portion of the data block is written
successfully, or (iii) a misdirected write, wherein the data is
written to either the wrong disk or the wrong location on
disk, thus overwriting and corrupting data [3,15].
Checksum mismatches can be detected anytime a disk block is read (file system reads,
data scrubs, RAID reconstruction and so on).
Checksum mismatches (CMs): This corruption class refers to cases where the
corruption is detected from mismatched data and checksum. The cause
could be
(i) data content corrupted by components within the data path,
or (ii) a torn write, wherein only a portion of the data block is written
successfully, or (iii) a misdirected write, wherein the data is
written to either the wrong disk or the wrong location on
disk, thus overwriting and corrupting data [3,15].
Checksum mismatches can be detected anytime a disk block is read (file system reads,
data scrubs, RAID reconstruction and so on).
 Identity discrepancies (IDs): This corruption class refers to a mismatch
detected when a disk block identity check is performed during a file
system read. The cause could be
(i) a lost write, which typically occurs because a write destined for
disk is not written but thought of as written,
or (ii) a misdirected write, where the original disk location is not updated.
We are aware of actual cases when the disk firmware replied successfully
to a write that was never written to stable media.
Identity discrepancies can be detected only during file system reads.
Identity discrepancies (IDs): This corruption class refers to a mismatch
detected when a disk block identity check is performed during a file
system read. The cause could be
(i) a lost write, which typically occurs because a write destined for
disk is not written but thought of as written,
or (ii) a misdirected write, where the original disk location is not updated.
We are aware of actual cases when the disk firmware replied successfully
to a write that was never written to stable media.
Identity discrepancies can be detected only during file system reads.
 Parity inconsistencies (PIs): This corruption class refers to a mismatch
between the parity computed from data blocks and the parity stored
on disk despite the individual checksums being valid.
This error could be caused by lost or misdirected writes, in-memory corruptions,
processor miscalculations, and software bugs. Parity inconsistencies
are detected only during data scrubs.
Parity inconsistencies (PIs): This corruption class refers to a mismatch
between the parity computed from data blocks and the parity stored
on disk despite the individual checksums being valid.
This error could be caused by lost or misdirected writes, in-memory corruptions,
processor miscalculations, and software bugs. Parity inconsistencies
are detected only during data scrubs.
Our study primarily focuses on checksum mismatches, since we find that these
corruptions occur much more frequently.
3 Methodology
This section describes some terminology, our data collection and
analysis methodology, and notation used to discuss our results.
We use the following terms in the remaining sections.
- Disk class
- Enterprise Class or nearline disk drives with respectively
Fibre Channel and ATA interfaces.
- Disk family
- A particular disk drive product. The same
product (and hence a disk family) may be offered in different capacities.
Typically, disks in the same family only differ in the number
of platters and/or read/write heads [17].
- Disk model
- The combination of a disk family and a
particular disk size. Note that this term does not imply an analytical or
simulation model.
- Disk age
- The amount of time a disk has been in the field
since its ship date, rather than the manufacture date. In practice
these these two values are typically within a month of each other.
- Corrupt block
- This term refers to a 4-KB file system block with a checksum mismatch.
- Corrupt disk
- This term is used to refer to a disk drive that has
at least one corrupt block.
We now describe our data collection and analysis methodology and
some limitations.
Data collection: The storage system has a built-in, low-overhead mechanism called
Autosupport to log
important system events back to a central repository. These messages
can be enabled for a variety of system events including disk errors.
Not all customers enable logging, although a large percentage do.
Those that do, sometimes do so only after some period of initial use.
These logs allow customized support based on observed events.
Although these logs are primarily intended for support,
they have also been utilized for analyzing various disk errors.
In addition to our corruption study, this repository (the ``Network Appliance Autosupport Database'')
has been used in disk failure [11] and
latent sector error [2] studies.
Analysis: We study corruption instances that were logged
in tens of thousands of storage systems for a period of 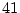 months starting in January 2004.
These systems belong to a range of different models, run different versions
of storage-controller software (perhaps with one or more updates during the study period) and
contain many different models or versions of hardware components.
In order to have a complete history of the activities of the disks
used in the study, we constrain our sample to only those disks that were shipped
after January 2004. Our sample consists of
months starting in January 2004.
These systems belong to a range of different models, run different versions
of storage-controller software (perhaps with one or more updates during the study period) and
contain many different models or versions of hardware components.
In order to have a complete history of the activities of the disks
used in the study, we constrain our sample to only those disks that were shipped
after January 2004. Our sample consists of 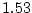 million disk drives.
These drives belong to 14 disk
families and 31 distinct models.
To derive statistically significant results, we often further
constrain the sample set depending on the analysis being performed.
For example, we sometimes use shorter time periods for our analysis so
as to maximize the number of models we can study; clearly not
all disk families and models have been in the field for the same duration.
The disk models we consider for each study may have one of the
following constraints:
million disk drives.
These drives belong to 14 disk
families and 31 distinct models.
To derive statistically significant results, we often further
constrain the sample set depending on the analysis being performed.
For example, we sometimes use shorter time periods for our analysis so
as to maximize the number of models we can study; clearly not
all disk families and models have been in the field for the same duration.
The disk models we consider for each study may have one of the
following constraints:
 Model has at least 1000 disks in the field for time
period being considered.
Model has at least 1000 disks in the field for time
period being considered.
 Model has at least 1000 disks in the field and at least
15 corrupt disks for time being considered.
Model has at least 1000 disks in the field and at least
15 corrupt disks for time being considered.
The first constraint is used for studies of factors that impact checksum mismatches, while
other studies use the second constraint.
In addition to the constraints on the model sample, we often restrict
our data to include only the first 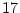 months since a drive was shipped.
This helps make results more comparable, since many of the drives in
the study were shipped on different dates and have been in the field
for different amounts of time.
months since a drive was shipped.
This helps make results more comparable, since many of the drives in
the study were shipped on different dates and have been in the field
for different amounts of time.
While we usually present data for individual disk models, we
sometimes also report averages (mean values) for nearline disks and enterprise class disks.
Since the sample size for different disk models per disk class varies
considerably, we weigh the average by the sample size of each
disk model in the respective class.
Limitations:
The study has a few limitations that mostly stem from the data
collection process.
First, for a variety of reasons, disks may be
removed from the system. Our study includes those disks up to the
point of their removal from the system.
Therefore, we may not observe errors from otherwise error prone disks
after some period of time.
Second, since the logging infrastructure has been built with customized support as the
primary purpose, the data can be used to answer most but not all
questions that are interesting for a study such as ours.
For example,
while we can identify the exact disk when an error is detected during a scrub,
we cannot verify that every disk in the study has been scrubbed
periodically in the absence of errors.
We denote each disk drive model as 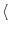 family-type
family-type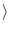 . For anonymization purposes, family is a single
letter representing the disk family (e.g., Quantum Fireball EX) and
type is a single number representing the disk's particular
capacity. Although capacities are anonymized, relative sizes within a
family are ordered by the number representing the capacity. For
example, n-2 is larger than n-1, and n-3 is larger than both n-1 and
n-2. The anonymized capacities do not allow comparisons across disk
families.
Disk families from A to E (upper case letters) are nearline disk families, while families from f to o (lower case
letters) are enterprise class disk families.
Lines on graphs labeled NL and ES represent the weighted
average for nearline and enterprise class disk models respectively.
. For anonymization purposes, family is a single
letter representing the disk family (e.g., Quantum Fireball EX) and
type is a single number representing the disk's particular
capacity. Although capacities are anonymized, relative sizes within a
family are ordered by the number representing the capacity. For
example, n-2 is larger than n-1, and n-3 is larger than both n-1 and
n-2. The anonymized capacities do not allow comparisons across disk
families.
Disk families from A to E (upper case letters) are nearline disk families, while families from f to o (lower case
letters) are enterprise class disk families.
Lines on graphs labeled NL and ES represent the weighted
average for nearline and enterprise class disk models respectively.
We present data as the probability of developing 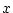 checksum mismatches for a
particular sample of disks. The notation
checksum mismatches for a
particular sample of disks. The notation
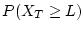 denotes the probability of a disk
developing at least
denotes the probability of a disk
developing at least 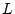 checksum mismatches within
checksum mismatches within
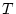 months since the disk's
first use in the field.
months since the disk's
first use in the field.
4 Checksum Mismatches
This section presents the results of our analysis of checksum mismatches. We first
provide basic statistics on the occurrence of checksum mismatches in the entire population of
disk drives.
We then examine various factors that affect the probability
of developing checksum mismatches. Next, we analyze various characteristics of checksum mismatches,
such as spatial locality. Further, we look for correlations between
occurrence of checksum mismatches and other system or disk errors. Finally, we
analyze the source of the disk requests that discovered the mismatches.
During the 41-month period covered by our data we observe a total of
about 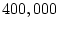 checksum mismatches.
Of the total sample of
checksum mismatches.
Of the total sample of 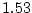 million disks, 3855 disks developed checksum mismatches -
3088 of the
million disks, 3855 disks developed checksum mismatches -
3088 of the 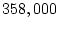 nearline disks (0.86%) and 767 of the
nearline disks (0.86%) and 767 of the 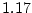 million enterprise class disks (0.065%).
Using our probability representation,
million enterprise class disks (0.065%).
Using our probability representation,
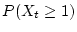 = 0.0086
for nearline disks, and
= 0.0086
for nearline disks, and
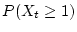 = 0.00065 for enterprise class disks
without any restriction on time,
= 0.00065 for enterprise class disks
without any restriction on time, 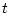 .
This indicates that nearline disks may be more susceptible to corruption leading to checksum mismatches than
enterprise class disks. On average, each disk developed 0.26 checksum mismatches.
Considering only corrupt disks, that is disks that experienced at least one
checksum mismatch, the mean number of mismatches per disk is 104, the median
is 3 and the mode (i.e. the most frequently observed value) is 1
mismatch per disk. The maximum number of mismatches observed for
any single drive is 33,000.
.
This indicates that nearline disks may be more susceptible to corruption leading to checksum mismatches than
enterprise class disks. On average, each disk developed 0.26 checksum mismatches.
Considering only corrupt disks, that is disks that experienced at least one
checksum mismatch, the mean number of mismatches per disk is 104, the median
is 3 and the mode (i.e. the most frequently observed value) is 1
mismatch per disk. The maximum number of mismatches observed for
any single drive is 33,000.
We examine the dependence of checksum mismatches on various factors:
disk class, disk model, disk age, disk size, and workload.
Figure 2:
Impact of disk age on nearline disks. The probability that a disk develops checksum mismatches as it
ages is shown for nearline disk models. Note that the probability is cumulative.
![\includegraphics[width=3.2in]{figures/age-ata.eps}](img27.png)
|
Figure 3:
Impact of disk age on enterprise class disks. The probability that a disk develops checksum mismatches as it
ages is shown for enterprise class disk models. Note that the probability is cumulative.
![\includegraphics[width=3.3in]{figures/age-fc-1.eps}](img28.png)
![\includegraphics[width=3.3in]{figures/age-fc-2.eps}](img29.png)
|
Figures 2 and 3 show the probability of
a disk developing checksum mismatches as it ages for nearline and enterprise class disks
respectively. The graphs plot the cumulative distribution function of
the time until the first checksum mismatch occurs. The figures can be
represented as
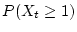 for
for 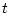 = {3, 6, 9, 12, 15, 17}
months, i.e., the probability of at least one checksum mismatch after
= {3, 6, 9, 12, 15, 17}
months, i.e., the probability of at least one checksum mismatch after 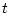 months. Note the different Y-axis scale for the nearline and enterprise class disks.
months. Note the different Y-axis scale for the nearline and enterprise class disks.
We see from the figures that checksum mismatches depend on disk class, disk model
and disk age.

Figure 2 (line `NL' - Nearline average) shows that
0.66% of nearline disks develop at least one mismatch during the first 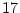 months in the field (
months in the field (
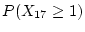 = 0.0066), while
Figure 3(b) (line `ES') indicates that only 0.06% of
enterprise class disks develop a mismatch during that time (
= 0.0066), while
Figure 3(b) (line `ES') indicates that only 0.06% of
enterprise class disks develop a mismatch during that time (
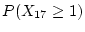 =
0.0006).
=
0.0006).
We see in Figure 2 that there is an order of magnitude
difference between models `C-1' and `E-2' for developing at least one
checksum mismatch after 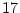 months; i.e.,
months; i.e.,
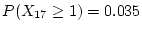 for `C-1'
and
for `C-1'
and 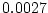 for `E-2'.
for `E-2'.
On average, as nearline disks age, the probability of developing a checksum mismatch is fairly constant, with some variation across the models. As enterprise class disks age, the probability of developing the first checksum mismatch decreases
after about 6-9 months and then stabilizes.
Figure 4:
The impact of disk size. The figures show the fraction of disks with at least one checksum mismatch within  months of shipping to the field for (a) nearline disk models, and (b) enterprise class disk models.
months of shipping to the field for (a) nearline disk models, and (b) enterprise class disk models.
![\includegraphics[width=3.3in]{figures/size-ata.eps}](img37.png)
![\includegraphics[width=3.3in]{figures/size-fc.eps}](img38.png)
|
Figure 4 presents the fraction of disks that develop
checksum mismatches within  months of their ship-date (i.e., the rightmost data
points from Figures 2 and 3;
months of their ship-date (i.e., the rightmost data
points from Figures 2 and 3;
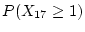 ). The disk models are grouped within their
families in increasing size.
Since the impact of disk size on the fraction of disks that
develop checksum mismatches is not constant across
all disk families (it occurs in only 7 out of 10 families), we conclude that
disk size does not necessarily impact the probability of developing
checksum mismatches.
). The disk models are grouped within their
families in increasing size.
Since the impact of disk size on the fraction of disks that
develop checksum mismatches is not constant across
all disk families (it occurs in only 7 out of 10 families), we conclude that
disk size does not necessarily impact the probability of developing
checksum mismatches.
The systems in the study collect coarse workload data including the number
of read and write operations, and the number of blocks read and
written for each week of our study. To study the effect of workload
on checksum mismatches, we computed the correlation coefficient between the
workload data and the number of checksum mismatches observed in the system.
We find that in all cases the correlation coefficient is less than 0.1
(in fact, in most cases less than 0.001), indicating no significant
correlation between workload and checksum mismatches.
However, these results might be due to having only coarse per-system rather
than per-drive workload data.
A system consists of at least 14 disks and can have as many as several
hundred disks. Aggregating data across a number of disks might blur
existing correlations between an individual drive's workload and
corruption behavior.
In this subsection, we explore various characteristics of checksum mismatches. First,
we analyze the number of mismatches developed by corrupt disks. Then, we
examine whether mismatches are independent occurrences. Finally, we examine
whether the mismatches have spatial or temporal locality.
Figure 5:
Checksum mismatches per corrupt disk. The fraction of corrupt disks as a function
of the number of checksum mismatches that develop within  months
after the ship date for (a) nearline disk models and (b) enterprise class disk
models. Note that the x-axis is not linear in scale - the lines in the graph
are used only to help distinguish the points of different disk models,
and their slopes are not meaningful.
months
after the ship date for (a) nearline disk models and (b) enterprise class disk
models. Note that the x-axis is not linear in scale - the lines in the graph
are used only to help distinguish the points of different disk models,
and their slopes are not meaningful.
![\includegraphics[width=3.3in]{figures/cpercdisk-ata.eps}](img40.png)
![\includegraphics[width=3.3in]{figures/cpercdisk-fc.eps}](img41.png)
|
Figure 5 shows the cumulative
distribution function of the number of checksum mismatches observed per
corrupt disk, i.e. the Y-axis shows the fraction of corrupt disks that have fewer than or equal to X number of corrupt blocks. The
figure can be represented as
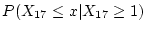 for
for 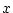 = {1, 2, 3, 4, 5, 10, 20, 50, 100, 200, 500, 1000}.
= {1, 2, 3, 4, 5, 10, 20, 50, 100, 200, 500, 1000}.
Figure 5 shows that a significant fraction of
corrupt disks (more than a third of all corrupt nearline disks and
more than a fifth of corrupt enterprise disks) develop only one
checksum mismatch. On the other hand, a small fraction of disks develop
several thousand checksum mismatches. The large variability in the number of
mismatches per drive is also reflected in the great difference
between the mean and median: while the median is only 3 mismatches per drive, the mean is 78.
A more detailed analysis reveals that the distributions exhibit
heavy tails. A large fraction of the total number of checksum mismatches observed in our study is experienced by a very small
fraction of the corrupt disks. More precisely, 1% of the corrupt disks
(the top 1% corrupt disks with the largest number of mismatches)
produce more than half of all mismatches recorded in the data.
Figure 5(a) (line `NL') and
Figure 5(b) (line `ES') show that within
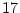 months 50% of corrupt disks (i.e., the median) develop about
2 checksum mismatches for nearline disks, but almost 10 for enterprise class disks.
The trend also extends to a higher percentage of corrupt disks. For example, 80%
of nearline corrupt disks have fewer than 20 mismatches, whereas 80% of
enterprise class disks have fewer than 100 mismatches.
Given that very few enterprise class disks develop checksum mismatches in the first place, in
the interest of reliability and availability, it might make sense to
replace the enterprise class disk when the first mismatch is detected.
months 50% of corrupt disks (i.e., the median) develop about
2 checksum mismatches for nearline disks, but almost 10 for enterprise class disks.
The trend also extends to a higher percentage of corrupt disks. For example, 80%
of nearline corrupt disks have fewer than 20 mismatches, whereas 80% of
enterprise class disks have fewer than 100 mismatches.
Given that very few enterprise class disks develop checksum mismatches in the first place, in
the interest of reliability and availability, it might make sense to
replace the enterprise class disk when the first mismatch is detected.
We find that the conditional probability of developing
further checksum mismatches, given that a disk has at least one mismatch,
is higher than the probability of developing the first
mismatch. For example, while the probability that a nearline disk will
develop one or more checksum mismatches in 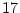 months is only 0.0066,
the conditional probability of developing more than 1 mismatch given that the disk already has one mismatch is as high as 0.6 (
months is only 0.0066,
the conditional probability of developing more than 1 mismatch given that the disk already has one mismatch is as high as 0.6 (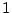 minus
minus 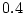 , the probability of exactly 1 block
developing a checksum mismatch in Figure 5).
, the probability of exactly 1 block
developing a checksum mismatch in Figure 5).
Finally, it is interesting to note that nearline disk model `E-1' is
particularly aberrant - around 30% of its corrupt disks develop more
than 1000 checksum mismatches. We are currently investigating this anomaly.
While most systems with checksum mismatches have only one corrupt disk, we do find a
considerable number of instances where multiple disks develop checksum mismatches within the same storage system. In fact, one of the systems in the
study that used nearline disks had 92 disks develop checksum mismatches. Taking the
maximum number of disks in the systems in the study into consideration, the probability
of 92 disks developing errors independently is less than 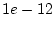 , much
less than
, much
less than 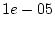 , the approximate fraction of systems represented by one system.
This dependence is perhaps indicative of a common corruption-causing component, such as a shelf
controller or adapter. We are aware of such components causing
corruptions.
, the approximate fraction of systems represented by one system.
This dependence is perhaps indicative of a common corruption-causing component, such as a shelf
controller or adapter. We are aware of such components causing
corruptions.
We measure spatial locality by examining whether each
corrupt block has another corrupt block (a neighbor) within
progressively larger regions (locality radius) around it on the
same disk. For example, if in a disk, blocks numbered 100, 200
and 500 have checksum mismatches, then blocks 100 and 200 have one
neighbor at a locality radius of 100, and all blocks (100, 200, and
500) have at least one neighbor at a locality radius of 300.
Figure 6:
Spatial Locality. The graphs show the probability of another checksum mismatch within a given
radius (disk block range) of one checksum mismatch.
Each figure also includes a line labeled ``Random'' corresponding to when the same number
of mismatches (as nearline and enterprise class respectively) are randomly distributed across
the block address space. Only disks with between 2 and 10 mismatches are included.
![\includegraphics[width=3.3in]{figures/spatial-ata.eps}](img51.png)
![\includegraphics[width=3.3in]{figures/spatial-fc.eps}](img52.png)
|
Figure 6 shows the percentage of corrupt blocks that
have at least one neighbor within different locality radii. Since a
larger number of checksum mismatches will significantly skew the numbers, we
consider only disks with 2 to 10 mismatches.
The figure can be represented as
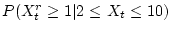 .
.
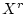 is the number of corrupt blocks in block numbers
is the number of corrupt blocks in block numbers
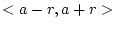 around corrupt block
around corrupt block 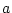 (but excluding
(but excluding 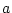 itself). The values for radius
itself). The values for radius 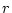 are
{1, 10, 100, ..., 100M} blocks, and
are
{1, 10, 100, ..., 100M} blocks, and
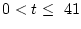 months. The
figure also includes a line Random that signifies the line that
would be obtained if the checksum mismatches were randomly distributed across
the block address space. This line can be used as a comparison point
against the other lines. Note that this line is at
months. The
figure also includes a line Random that signifies the line that
would be obtained if the checksum mismatches were randomly distributed across
the block address space. This line can be used as a comparison point
against the other lines. Note that this line is at 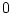 for most
of the graph, signifying that there is no spatial locality for a
random distribution.
for most
of the graph, signifying that there is no spatial locality for a
random distribution.
For the actual data for the different disk models, we see that
most disk models are much higher on the graph than Random when the x-axis value is 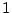 ;
for more than 50% of the corrupt blocks in nearline disks and more than 40% of the corrupt blocks in enterprise class disks,
the immediate neighboring block also has a checksum mismatch (on
disks with between 2 and 10 mismatches). These percentages indicate very high
spatial locality.
;
for more than 50% of the corrupt blocks in nearline disks and more than 40% of the corrupt blocks in enterprise class disks,
the immediate neighboring block also has a checksum mismatch (on
disks with between 2 and 10 mismatches). These percentages indicate very high
spatial locality.
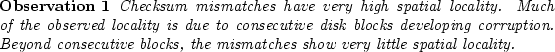
We see from the figures that, while the lines for the disk models start
at a very high value when the x-axis value is 1, they are almost flat
for most of the graph, moving steeply upwards to 1
only towards the end (x-axis values more than 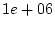 ).
This behavior shows that most of the spatial locality is due to
consecutive blocks developing checksum mismatches. However, it is important to
note that even when the consecutive mismatch cases are disregarded,
the distribution of the mismatches still has spatial locality.
).
This behavior shows that most of the spatial locality is due to
consecutive blocks developing checksum mismatches. However, it is important to
note that even when the consecutive mismatch cases are disregarded,
the distribution of the mismatches still has spatial locality.
Given the strong correlation between checksum mismatches in consecutive blocks, it is
interesting to examine the run length of consecutive
mismatches, i.e., how many consecutive blocks have mismatches. We
find that, among drives with at least 2 checksum mismatches(and no upper bound on mismatches), on average 3.4
consecutive blocks are affected. In some cases, the length of
consecutive runs can be much higher than the average. About 3% of drives
with at least 2 mismatches see one or more runs of 100 consecutive
blocks with mismatches. 0.7% of drives with at least 2 mismatches see one or
more runs of 1000 consecutive mismatches.
Figure 7:
Inter-arrival times. The graphs show the cumulative distribution of the inter-arrival times of checksum mismatches per minute.
The fraction of mismatches per model is plotted against time. The arrival times are binned by minute.
![\includegraphics[width=3.3in]{figures/inter-arrival-ata.eps}](img62.png)
![\includegraphics[width=3.3in]{figures/inter-arrival-fc.eps}](img63.png)
|
Figure 7 shows the fraction of checksum mismatches that arrive
(are detected) within 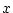 minutes of a previous mismatch. The figure
can be represented as
minutes of a previous mismatch. The figure
can be represented as
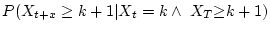 for
for 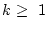 ,
,
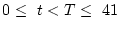 months,
and
months,
and
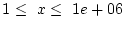 minutes.
minutes.
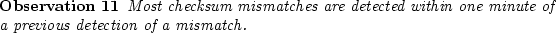
The figure shows that the temporal locality for detecting checksum mismatches is extremely high. This behavior may be an artifact of the manner in
which the detection takes place (by scrubbing) and the fact that many
mismatches are spatially local and are therefore likely to be
discovered together. Further analysis shows that this is not necessarily
the case.
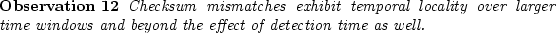
In order to remove the impact of detection time, we examine temporal locality
over larger time windows. For each drive, we first determine the
number of checksum mismatches experienced in each 2-week time window
that the drive was in
the field and then compute the autocorrelation function (ACF) on the resulting time series.
The autocorrelation function (ACF) measures the correlation of a random variable
with itself at different time lags 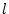 . The ACF can be used to determine whether the number of
mismatches in one two-week period of our time-series is correlated with the number of
mismatches observed
. The ACF can be used to determine whether the number of
mismatches in one two-week period of our time-series is correlated with the number of
mismatches observed 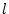 2-week periods later. The autocorrelation
coefficient can range between 1 (high positive correlation)
and -1 (high negative correlation). A value of zero would indicate no correlation,
supporting independence of checksum mismatches.
2-week periods later. The autocorrelation
coefficient can range between 1 (high positive correlation)
and -1 (high negative correlation). A value of zero would indicate no correlation,
supporting independence of checksum mismatches.
Figure 8:
Temporal Autocorrelation. The graph shows the autocorrelation function for the number of checksum mismatches
per 2-week time windows. This representation of the data allows us to study temporal locality of mismatches at larger time-scales without
being affected by the time of detection.
|
|
Figure 8 shows the resulting ACF. The graph presents
the average ACF across all drives in the study that were in the field
for at least 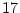 months and experienced checksum mismatches in at least two
different 2-week windows. Since the results are nearly
indistinguishable for nearline and enterprise class drives, individual results are not
given. If checksum mismatches in different 2-week periods were
independent (no temporal locality on bi-weekly and larger time-scales)
the graph would be close to zero at all lags. Instead we observe
strong autocorrelation even for large lags in the range of up to 10
months.
months and experienced checksum mismatches in at least two
different 2-week windows. Since the results are nearly
indistinguishable for nearline and enterprise class drives, individual results are not
given. If checksum mismatches in different 2-week periods were
independent (no temporal locality on bi-weekly and larger time-scales)
the graph would be close to zero at all lags. Instead we observe
strong autocorrelation even for large lags in the range of up to 10
months.
Our system logs data on various other system and disk errors as well.
We attempted to establish correlations for checksum mismatches with system resets, latent sector errors,
and not-ready-conditions.
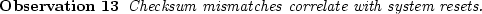
The conditional probability of a system reset at some point of time, given
that one of the disks in the system has a checksum mismatch, is about 3.7
times the unconditional probability of a system reset.
After a system reset, the system performs higher-level recovery operations;
for example, a thorough file system integrity check may be run.

The probability of a disk developing latent sector errors,
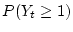 , is 0.137
for nearline disks and 0.026 for enterprise class disks (
, is 0.137
for nearline disks and 0.026 for enterprise class disks (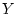 is the number of latent sector errors,
is the number of latent sector errors,
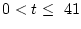 months). The conditional probability
months). The conditional probability
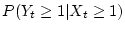 = 0.195 for nearline disks and
0.0556 for enterprise class disks. Thus, the conditional probability of a latent sector error,
given that a disk has checksum mismatch, is about 1.4 times the unconditional
probability of a latent sector error in the case of nearline disks and about 2.2 times
the unconditional probability for enterprise class disks. These values indicate
a weak positive correlation between the two disk errors.
= 0.195 for nearline disks and
0.0556 for enterprise class disks. Thus, the conditional probability of a latent sector error,
given that a disk has checksum mismatch, is about 1.4 times the unconditional
probability of a latent sector error in the case of nearline disks and about 2.2 times
the unconditional probability for enterprise class disks. These values indicate
a weak positive correlation between the two disk errors.
In order to test the statistical significance of this correlation we
performed a chi-square test for independence.
We find that we can with high confidence reject the hypothesis that checksum mismatches and latent sector errors are
independent, both in the case of nearline disks and enterprise class disks (confidence level of more than 99.999%).
Interestingly, the results vary if we repeat the chi-square test
separately for each individual disk model (including only models that had at least
15 corrupt disks). We can reject independence with high certainty
(at least 95% confidence) for only four out of seven nearline models
(B-1, C-1, D-1, E-2) and two out of seven enterprise class models (l-1, n-3).
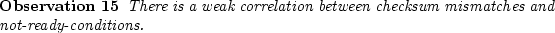
The probability of a disk developing not-ready-conditions,
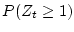 , is 0.18 for
nearline and 0.03 for enterprise class disks.
, is 0.18 for
nearline and 0.03 for enterprise class disks.
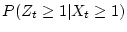 is
0.304 for nearline and 0.0155 for enterprise class disks. Thus, the conditional
probability of a not-ready-condition, given that a disk has checksum mismatch, is about 1.7 times
the unconditional probability of a not-ready-condition in the case of nearline disks
and about 0.5 times the unconditional probability for enterprise class disks. These values indicate mixed behavior - a weak positive
correlation for nearline disks and a weak negative correlation for enterprise class disks.
is
0.304 for nearline and 0.0155 for enterprise class disks. Thus, the conditional
probability of a not-ready-condition, given that a disk has checksum mismatch, is about 1.7 times
the unconditional probability of a not-ready-condition in the case of nearline disks
and about 0.5 times the unconditional probability for enterprise class disks. These values indicate mixed behavior - a weak positive
correlation for nearline disks and a weak negative correlation for enterprise class disks.
In order to test the statistical significance of the correlation between not-ready-conditions and checksum mismatches,
we again perform a chi-square test for independence. We find that for both nearline and enterprise disks we can
reject the hypothesis that not-ready conditions and random corruptions are independent with more than 96% confidence.
We repeat the same test separately for each disk model (including only models that had at least 15 corrupt disks).
In the case of nearline disks, we can reject the independence hypothesis for all models, except for two (A-1 and B-1)
at the 95% confidence level. However, in the case of enterprise class disks, we cannot reject the independece
hypothesis for any of the individual models at a significant confidence level.
Figure 9:
Request type analysis. The distribution of requests that discover checksum mismatches across
the request types scrub, non-file sytstem read (say, disk copy), write (of partial RAID stripe), file system read, and RAID reconstruction.
![\includegraphics[width=3.3in]{figures/request.eps}](img80.png)
|
Figure 9 shows the distribution of requests that
detect checksum mismatches into different request types. There are five types of requests that
discover checksum mismatches: (i) Reads by the file system (FS Read) (ii)
Partial RAID stripe writes by the RAID layer (Write) (iii)
Reads for disk copy operations (Non-FS Read) (iv) Reads for
data scrubbing (Scrub), and (v) Reads performed during RAID
reconstruction (Reconstruction).
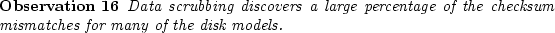
We see that on the average data scrubbing discovers about 49% of checksum mismatches in nearline disks (NL in the figure), and 73% of the checksum mismatches in enterprise class disks
(ES in the figure). It is quite possible that these checksum mismatches may not have
been discovered in the absence of data scrubbing, potentially exposing the
system to double failures and data loss. We do not know the precise cause
for the disparity in percentages between nearline and enterprise class disks; one possibility
this data suggests is that systems with nearline disks perform many more disk copy operations
(Non-FS Read), thus increasing the percentage for that request type.
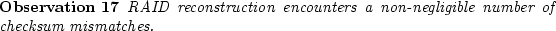
Despite the use of data scrubbing, we find that RAID reconstruction
discovers about 8% of the checksum mismatches in nearline disks.
For some models more than 20RAID reconstruction.
This observation
implies that (a) data scrubbing should be performed more aggressively,
and (b) systems should consider protection against double disk
failures [1,4,5,9,10,12].
In this subsection, we compare the characteristics of checksum mismatches, with
the characteristics of latent sector errors, identified in a
recent study [2].
Table 2:
Checksum mismatches vs. Latent sector errors. This table compares our findings on checksum mismatches with
characteristics of latent sector errors identified by a recent study, for both nearline and enterprise class disk models. In addition to listed correlations, latent sector errors and checksum mismatches
share a weak positive correlation with each other.
| Characteristic |
Latent sector errors |
Checksum mismatches |
| |
Nearline |
Enterprise |
Nearline |
Enterprise |
| % disks affected per year (avg) |
9.5% |
1.4% |
0.466% |
0.042% |
| As disk age increases, P(1st error) |
increases |
remains constant |
remains fairly constant |
decreases, then stabilizes |
| As disk size increases, P(1st error) |
increases |
increases |
unclear |
unclear |
| No. of errors per disk with errors (80 percentile) |
about 50 |
about 50 |
about 100 |
about 100 |
| Are errors independent ? |
No |
No |
No |
No |
| Spatial locality |
at 10 MB |
at 10 MB |
at 4KB |
at 4KB |
| Temporal locality |
very high |
very high |
very high |
very high |
| Known Correlations |
not-ready-conditions |
recovered errors |
system resets, not-ready-conditions |
system resets, not-ready-conditions |
|
Table 2 compares the behavior of checksum mismatches and latent sector errors. Some
of the interesting similarities and differences are as follows.
Frequency: The probability of developing checksum mismatches is about an
order of magnitude smaller than that for latent sector errors. However, given that
customers use a few million disk drives, it is important to handle
both kinds of errors. Also, since latent sector errors are more likely to be
detected, it is more likely that an undetected checksum mismatch will lead to data
loss.
Disk model: The nearline disk model E-2 has the highest
percentage of disks developing latent sector errors, but the lowest percentage of
disks developing checksum mismatches within the set of nearline disk models.
Impact of disk class: For both latent sector errors and checksum mismatches, enterprise class disks
are less likely to develop an error than nearline disks. Surprisingly,
however, in both cases, enterprise class disks develop a higher number of
errors than nearline disks, once an error has developed.
Spatial locality: Both latent sector errors and checksum mismatches show high spatial
locality. Interestingly, the difference in the locality radii that
capture a large fraction of errors - about 10 MB for latent sector errors versus consecutive
blocks for checksum mismatches - provides an insight into how the two errors could
be caused very differently. Latent sector errors may be caused by media scratches
that could go across tracks as opposed to consecutive sectors (hence a
larger locality radius) while consecutive blocks may have checksum mismatches simply
because the corruption(s) occurred when they were written together or
around the same time.
5 Other Data Corruptions
This section presents our results on the frequency of occurrence for
two corruption classes: identity discrepancies, and parity inconsistencies.
These corruption classes are described in Section 2.3.
Figure 10:
Identity Discrepancies. The figures show the fraction of disks with at least one identity discrepancy within 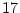 months of shipping to the field for (a) nearline disk models, and (b) enterprise class disk models.
months of shipping to the field for (a) nearline disk models, and (b) enterprise class disk models.
![\includegraphics[width=3.3in]{figures/lw-ata.eps}](img83.png)
![\includegraphics[width=3.3in]{figures/lw-fc.eps}](img84.png)
|
These errors were detected in a total 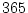 disks out of
the
disks out of
the 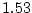 million disks. Figure 10 presents the
fraction of disks of each disk model that developed identity discrepancies in
million disks. Figure 10 presents the
fraction of disks of each disk model that developed identity discrepancies in
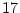 months. We see that the fraction is more than an order
of magnitude lower than that for checksum mismatches for both nearline and enterprise class disks.
months. We see that the fraction is more than an order
of magnitude lower than that for checksum mismatches for both nearline and enterprise class disks.
Since the fraction of disks that develop identity discrepancies is very low, the system
recommends replacement of the disk once the first identity discrepancy is detected.
It is important to note, that even though the number of identity discrepancies are
small, silent data corruption would have occurred if not for the
validation of the stored contextual file system information.
Figure 11:
Parity Inconsistencies. The figures show the fraction of disks with at least one parity inconsistency within 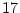 months of shipping to the field for (a) nearline disk models, and (b) enterprise class disk models.
months of shipping to the field for (a) nearline disk models, and (b) enterprise class disk models.
![\includegraphics[width=3.3in]{figures/pi-ata.eps}](img86.png)
![\includegraphics[width=3.3in]{figures/pi-fc.eps}](img87.png)
|
These errors are detected by data scrubbing. In the
absence of a second parity disk, one cannot identify which disk is at
fault. Therefore, in order to prevent potential data loss on disk
failure, the system fixes the inconsistency by rewriting parity.
This scenario provides further motivation for double-parity protection
schemes.
Figure 11 presents the fraction of disks of each
disk model that caused parity inconsistencies within 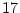 months since
ship date. The fraction is 4.4 times lower than that for checksum mismatches in the
case of nearline disks and about 3.5 times lower than that for
checksum mismatches for enterprise class disks.
months since
ship date. The fraction is 4.4 times lower than that for checksum mismatches in the
case of nearline disks and about 3.5 times lower than that for
checksum mismatches for enterprise class disks.
These results assume that the parity disk is at fault. We believe
that counting the number of incorrect parity disks reflect the
actual number of error disks since: (i) entire shelves of disks are
typically of the same age and same model, (ii) the incidence of
these inconsistencies is quite low; hence, it is unlikely that
multiple different disks in the same RAID group would be at fault.
6 Experience
This section uses results from our analysis of corruption and leverages our experience
in protecting against data corruption to develop insights into how storage
systems can be designed to deal with corruption.
First, we describe unexplained corruption phenomena and
anecdotal insight into the causes of corruption, and then
we discuss the lessons learned from our experience.
Finally, we list some questions that could be looked at in
future data analysis.
From analysis, we find that specific block numbers could be much more likely to
experience corruption than other block numbers. This behavior was observed for the
disk model `E-1'. Figure 12 presents for each block number, the
number of disk drives of disk model `E-1' that developed a checksum mismatch at that block number.
We see in the figure that many disks develop corruption for a specific set of block numbers. We also
verified that (i) other disk models did not develop multiple checksum mismatches for the same set of
block numbers (ii) the disks that developed mismatches at the same block numbers belong
to different storage systems, and (iii) our software stack has no specific data structure that
is placed at the block numbers of interest.
These observations indicate that hardware or firmware bugs
that affect specific sets of block numbers might exist. Therefore,
RAID system designers may be well-advised to use staggered
stripes such that the blocks that form a stripe (providing the
required redundancy) are placed at different block numbers on
different disks.
We also observed a large number of block-specific errors on other
drive models. In at least one of these instances, the block
contained a heavily read and written file system metadata
structure - a structure akin to the superblock. This suggests the
importance of replicating important metadata structures [15,20].
Figure 12:
Distribution of errors across block numbers. For each disk block number, the number of disks of
disk model E-1 that develop checksum mismatches at that block number is shown. The units on the x-axis have been omitted in order
to anonymize the disk size of disk model E-1.
![\includegraphics[width=3.2in]{figures/e1blocknums.eps}](img88.png)
|
We have observed instances of the SATA/FC adapter causing data corruption in the case of
disk models A-1, D-1 and D-2. Thus, it is very likely that the numbers for these disk models
in Section 4 are influenced by faulty shelf controllers. Such behavior may also
point to why different disks in the same system may not have independent failure behavior with
respect to data corruption (Observation 9).
One of the disk drive models in the study had a bug specific to flushing
the disk's write cache. Upon reception of a cache flush command, the
disk drive sometimes returned success without committing the
data to stable storage on the disk medium. If, for any reason, the disk was then
power-cycled the data just written was lost. However,
thanks to block identity protection (and RAID), the storage system did not lose data.
We present some of the lessons learned from the analysis
for corruption-proof storage system design. Some of these
lessons are specific to RAIDs, while others can be applied to file
systems as well.
 Albeit not as common as latent sector errors, data corruption does happen;
we observed more than
Albeit not as common as latent sector errors, data corruption does happen;
we observed more than 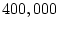 cases of checksum mismatches. For some drive models as many as
4% of drives develop checksum mismatches during the
cases of checksum mismatches. For some drive models as many as
4% of drives develop checksum mismatches during the 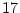 months examined. Similarly,
even though they are rare, identity discrepancies and parity inconsistencies do occur. Protection
offered by checksums and block identity information is
therefore well-worth the extra space needed to store them.
months examined. Similarly,
even though they are rare, identity discrepancies and parity inconsistencies do occur. Protection
offered by checksums and block identity information is
therefore well-worth the extra space needed to store them.
 A significant number (8% on average)
of corruptions are detected during RAID reconstruction,
creating the possibility of data loss. In this case, protection
against double disk failures [1,4,5,9,10,12] is necessary to
prevent data loss. More aggressive scrubbing can speed
the detection of errors, reducing the likelihood of an error during a
reconstruction.
A significant number (8% on average)
of corruptions are detected during RAID reconstruction,
creating the possibility of data loss. In this case, protection
against double disk failures [1,4,5,9,10,12] is necessary to
prevent data loss. More aggressive scrubbing can speed
the detection of errors, reducing the likelihood of an error during a
reconstruction.
 Although, the probability of developing a corruption is lower for enterprise class drives,
once they develop a corruption, many more are likely to follow. Therefore, replacing an
enterprise class drive on the first detection of a corruption might make sense
(drive replacement cost may not be a huge factor since the probability of first corruption is low).
Although, the probability of developing a corruption is lower for enterprise class drives,
once they develop a corruption, many more are likely to follow. Therefore, replacing an
enterprise class drive on the first detection of a corruption might make sense
(drive replacement cost may not be a huge factor since the probability of first corruption is low).
 Some block numbers are much more likely to be affected by corruption than others,
potentially due to hardware or firmware bugs that affect specific sets of block
numbers. RAID system designers might be well advised to use staggered stripes
such that the blocks that form the stripe are not stored at the same or nearby
block number.
Some block numbers are much more likely to be affected by corruption than others,
potentially due to hardware or firmware bugs that affect specific sets of block
numbers. RAID system designers might be well advised to use staggered stripes
such that the blocks that form the stripe are not stored at the same or nearby
block number.
 Strong spatial locality suggests that redundant data structures
should be stored distant from each other.
Strong spatial locality suggests that redundant data structures
should be stored distant from each other.
 The high degree of spatial and temporal locality also begs the
question of whether many corruptions occur at the exact same time, perhaps when all blocks are
written as part of the same disk request. This hypothesis suggests that
important or redundant data structures that are used for recovering data
on corruption should be written as part of different write requests
spaced over time.
The high degree of spatial and temporal locality also begs the
question of whether many corruptions occur at the exact same time, perhaps when all blocks are
written as part of the same disk request. This hypothesis suggests that
important or redundant data structures that are used for recovering data
on corruption should be written as part of different write requests
spaced over time.
 Strong spatial and temporal locality (over long time periods) also suggests that it might be worth
investigating how the locality can be leveraged for smarter scrubbing, e.g. trigger a scrub before it's
next scheduled time, when probability of corruption is high or selective scrubbing
of an area of the drive that's likely to be affected.
Strong spatial and temporal locality (over long time periods) also suggests that it might be worth
investigating how the locality can be leveraged for smarter scrubbing, e.g. trigger a scrub before it's
next scheduled time, when probability of corruption is high or selective scrubbing
of an area of the drive that's likely to be affected.
 Failure prediction algorithms in systems should take into
account the correlation of corruption with other errors such as latent sector errors,
increasing the probability of one error when an instance of the other is found.
Failure prediction algorithms in systems should take into
account the correlation of corruption with other errors such as latent sector errors,
increasing the probability of one error when an instance of the other is found.
Future data analysis studies could focus on questions on data corruption and its causes
that our current study does not answer. We discuss some such questions below.
(i) Our study looks at corruption numbers
across different disk models. We find that the numbers vary significantly
across disk models, suggesting that disks (and their adapters)
may directly or indirectly cause corruption most of the time. However, disks are only one of the storage stack
components that could potentially cause corruption. A recent study shows that other storage subsystem
components do have a significant impact on storage failures [11]).
A future study could focus on corruption numbers across different models or versions
of all hardware and software components. Such a study may also help
pinpoint the exact sources of data corruption.
(ii) The impact of workload on the prevalence of data corruption is unclear, especially due
to the lack of fine-grained disk-level workload information. Future studies may focus on
obtaining this information along with recording disk corruption occurrences.
7 Related Work
There are very few studies of disk errors. Most disk fault studies
examine either drive failures [14,16,17,18]
or latent sector errors [2].
Of the large scale drive failure studies, Schroeder and
Gibson [16] analyze data from about 100,000 disks over a
five year time period. They find that failure rate increases over
time, and error rates are not constant with disk age. Pinheiro et
al. [14] analyze data associated with over 100,000 disks
over a nine month period. They use this data to analyze the
correlation of disk failures to environmental factors and usage
patterns. They find that the annualized failure rate is significantly
higher for drives after the first year.
Jiang et al. [11] study various
aspects of storage subsystem failures. For example, they determine that
subsystem components other than disks cause a significant fraction of observed
failures.
Shah and
Elerath [7,17,18]
have performed a number of studies on the reliability of disk drives.
They find from these studies that there are many factors, including disk drive
vintage, which influence the failure rate
of disks and that there is a large variation between disk models and
families.
There is a large body of work regarding techniques for detecting and
recovering from data corruption.
Sivathanu et. al [19] survey data integrity
techniques within storage systems, and classify integrity violation
types and detection and correction schemes.
Prabhakaran et al. [15] develop a taxonomy to
classify file system failures. They find that many of
the file systems tested do not detect nor recover from most disk
corruption errors.
Many of the file systems tested use some form of disk block type
checking (e.g., a magic-number for metadata), however lost or
misdirected writes still cause corruption if the block's new type
matched its previous type.
Using checksums to protect data integrity is an old concept,
especially in communication systems. The Tandem NonStop
Server [3] was designed to use end-to-end
checksums at the host, writing it to disk with the data and verifying
it on read.
However, the majority of file systems today still rely on disk
drives to report internal errors.
Two of the more recent file systems to use checksums to detect
corrupted data include Sun's ZFS [21] and Google's
GFS [8].
ZFS uses 64-bit checksums to validate the data path. A checksum is
stored with every block pointer and is validated by the file system
layer. If a checksum error is encountered and a mirrored copy is
available, the mirrored copy is used to correct the data.
GFS also uses checksums to protect data integrity. GFS distributes
data across chunk servers that break the chunks into 64KB data blocks,
each protected by a 32-bit checksum. On a checksum
mismatch, the correct data is retrieved from a replica.
Both file systems use some form of periodic scrubbing to validate
data.
8 Conclusion
We have analyzed data corruption instances detected in 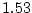 million disks
used in our production storage systems. We classified these instances into
three classes: checksum mismatches, identity discrepancies, and parity inconsistencies.
We find that only a small fraction of disks develop checksum mismatches.
An even smaller fraction are due to identity discrepancies or parity inconsistencies.
Even with the small number of errors observed it is still critical to
detect and recover from these errors since data loss is rarely
tolerated in enterprise-class and archival storage systems.
million disks
used in our production storage systems. We classified these instances into
three classes: checksum mismatches, identity discrepancies, and parity inconsistencies.
We find that only a small fraction of disks develop checksum mismatches.
An even smaller fraction are due to identity discrepancies or parity inconsistencies.
Even with the small number of errors observed it is still critical to
detect and recover from these errors since data loss is rarely
tolerated in enterprise-class and archival storage systems.
We have identified various characteristics of checksum mismatches, including
(i) the probability of developing the first checksum mismatch is almost an
order of magnitude higher for nearline disks than for enterprise class disks,
(ii) checksum mismatches are not independent and the number of mismatches per
disk follows a heavy-tailed distribution,
and (iii) checksum mismatches also show high spatial and temporal locality,
encouraging system designers to develop schemes that spread
redundant data with respect to both the on-disk location and
time at which they are written.
We have obtained insights for corruption-proof storage design from
the statistical and anecdotal evidence we have collected.
We believe that such insights are essential for designing highly
reliable storage systems.
This material is based upon work supported by the National Science Foundation
under the following grants:
CCF-0621487,
CNS-0509474,
CCR-0133456,
as well as by generous donations from Network Appliance.
We thank the Autosupport team at NetApp for their help
in gathering data. Members of the RAID
group including Atul Goel, Tomislav Grcanac, Rajesh Sundaram, Jim Taylor, and Tom Theaker
provided insightful comments on the analysis.
David Ford, Stephen Harpster, Steve Kleiman, Brian Pawlowski and
members of the Advanced Technology Group provided
excellent input on the work.
Ramon del Rosario, Jon Elerath, Tim Emami, Aziz Htite, Hung Lu, and Sandeep Shah
helped understand characteristics of disks and systems in the study,
and mine Autosupport data.
Finally, we would like to thank
our shepherd Alma Riska and the anonymous reviewers
for their detailed comments that helped improve the paper.
Any opinions, findings, and conclusions or recommendations expressed in this
material are those of the authors and do not necessarily reflect the views
of NSF or other institutions.
- 1
-
G. A. Alvarez, W. A. Burkhard, and F. Cristian.
Tolerating Multiple Failures in RAID Architectures with Optimal
Storage and Uniform Declustering.
In Proceedings of the 24th Annual International Symposium on
Computer Architecture (ISCA '97), pages 62-72, Denver, Colorado, June 1997.
- 2
-
L. N. Bairavasundaram, G. R. Goodson, S. Pasupathy, and J. Schindler.
An Analysis of Latent Sector Errors in Disk Drives.
In Proceedings of the International Conference on Measurements
and Modeling of Computer Systems (SIGMETRICS'07), San Diego, California,
June 2007.
- 3
-
W. Bartlett and L. Spainhower.
Commercial Fault Tolerance: A Tale of Two Systems.
IEEE Transactions on Dependable and Secure Computing,
1(1):87-96, Jan. 2004.
- 4
-
M. Blaum, J. Brady, J. Bruck, and J. Menon.
EVENODD: An Optimal Scheme for Tolerating Double Disk Failures in
RAID Architectures.
In Proceedings of the 21st Annual International Symposium on
Computer Architecture (ISCA '94), pages 245-254, Chicago, Illinois, Apr.
1994.
- 5
-
P. Corbett, B. English, A. Goel, T. Grcanac, S. Kleiman, J. Leong, and
S. Sankar.
Row-diagonal parity for double disk failure correction.
In Proceedings of the 3rd USENIX Symposium on File and Storage
Technologies (FAST '04), pages 1-14, San Francisco, California, Apr. 2004.
- 6
-
M. H. Darden.
Data Integrity: The Dell|EMC Distinction.
https://www.dell.com/content/topics/global.aspx/power/
en/ps2q02_darden?c=us&cs=555&l=en&s=biz, May 2002.
- 7
-
J. G. Elerath and S. Shah.
Server Class Disk Drives: How Reliable Are They.
In The Proceedings of the 50th Annual Reliability and
Maintainability Symposium, pages 151-156, Los Angeles, California, Jan.
2004.
- 8
-
S. Ghemawat, H. Gobioff, and S.-T. Leung.
The Google File System.
In Proceedings of the 19th ACM Symposium on Operating Systems
Principles (SOSP '03), pages 29-43, Bolton Landing (Lake George), New York,
October 2003.
- 9
-
J. L. Hafner.
WEAVER Codes: Highly Fault Tolerant Erasure Codes for Storage
Systems.
In Proceedings of the 4th USENIX Symposium on File and Storage
Technologies (FAST '05), San Francisco, California, Dec. 2005.
- 10
-
J. L. Hafner, V. W. Deenadhayalan, K. Rao, and J. A. Tomlin.
Matrix Methods for Lost Data Reconstruction in Erasure Codes.
In Proceedings of the 4th USENIX Symposium on File and Storage
Technologies (FAST '05), San Francisco, California, Dec. 2005.
- 11
-
W. Jiang, C. Hu, A. Kanevsky, and Y. Zhou.
Is Disk the Dominant Contributor for Storage Subsystem Failures? A
Comprehensive Study of Failure Characteristics.
In Proceedings of the 6th USENIX Symposium on File and Storage
Technologies (FAST '08), San Jose, California, Feb. 2008.
- 12
-
C.-I. Park.
Efficient Placement of Parity and Data to Tolerate Two Disk Failures
in Disk Array Systems.
IEEE Transactions on Parallel and Distributed Systems,
6(11):1177-1184, Nov. 1995.
- 13
-
D. Patterson, G. Gibson, and R. Katz.
A Case for Redundant Arrays of Inexpensive Disks (RAID).
In Proceedings of the 1988 ACM SIGMOD Conference on the
Management of Data (SIGMOD '88), pages 109-116, Chicago, Illinois, June
1988.
- 14
-
E. Pinheiro, W. D. Weber, and L. A. Barroso.
Failure Trends in a Large Disk Drive Population.
In Proceedings of the 5th USENIX Symposium on File and Storage
Technologies (FAST '07), San Jose, California, Feb. 2007.
- 15
-
V. Prabhakaran, L. N. Bairavasundaram, N. Agrawal, H. S. Gunawi, A. C.
Arpaci-Dusseau, and R. H. Arpaci-Dusseau.
IRON File Systems.
In Proceedings of the 20th ACM Symposium on Operating Systems
Principles (SOSP '05), pages 206-220, Brighton, United Kingdom, Oct. 2005.
- 16
-
B. Schroeder and G. A. Gibson.
Disk Failures in the Real World: What Does an MTTF of 1,000,000
Hours Mean to You?
In Proceedings of the 5th USENIX Symposium on File and Storage
Technologies (FAST '07), San Jose, California, Feb. 2007.
- 17
-
S. Shah and J. G. Elerath.
Disk Drive Vintage and its Effect on Reliability.
In The Proceedings of the 50th Annual Reliability and
Maintainability Symposium, pages 163-167, Los Angeles, California, Jan.
2004.
- 18
-
S. Shah and J. G. Elerath.
Reliability Analyses of Disk Drive Failure Mechanisms.
In The Proceedings of the 51st Annual Reliability and
Maintainability Symposium, pages 226-231, Alexandria, Virginia, Jan. 2005.
- 19
-
G. Sivathanu, C. P. Wright, and E. Zadok.
Ensuring data integrity in storage: Techniques and applications.
In Proceedings of the ACM Workshop on Storage Security and
Survivability (StorageSS '05), pages 26-36, Fairfax, Virginia, November
2005.
- 20
-
M. Sivathanu, V. Prabhakaran, A. C. Arpaci-Dusseau, and R. H.
Arpaci-Dusseau.
Improving storage system availability with D-GRAID.
In Proceedings of the 3rd USENIX Symposium on File and Storage
Technologies (FAST '04), pages 15-30, San Francisco, California, Apr. 2004.
- 21
-
Sun Microsystems.
ZFS: The last word in file systems.
www.sun.com/2004-0914/feature/, 2006.
- 22
-
R. Sundaram.
The Private Lives of Disk Drives.
https://www.netapp.com/go/techontap/matl/sample/
0206tot_resiliency.html, Feb. 2006.
- 23
-
Information Technology: SCSI Primary Commands (SPC-2).
Technical Report T10 Project 1236-D Revision 5, Sept. 1998.
An Analysis of Data Corruption in the Storage Stack
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -transparent -local_icons -no_navigation main
The translation was initiated by Lakshmi Bairavasundaram on 2008-01-08
Lakshmi Bairavasundaram
2008-01-08
![]() , Garth R. Goodson
, Garth R. Goodson![]() , Bianca Schroeder
, Bianca Schroeder![]() ,
Andrea C. Arpaci-Dusseau
,
Andrea C. Arpaci-Dusseau![]() , Remzi H. Arpaci-Dusseau
, Remzi H. Arpaci-Dusseau![]()
![]() University of Wisconsin-Madison
University of Wisconsin-Madison ![]() Network Appliance, Inc.
Network Appliance, Inc. ![]() University of Toronto
University of Toronto
![\includegraphics[width=3.2in]{figures/checksum-fc-laksh.eps}](img13.png)
![\includegraphics[width=3.2in]{figures/checksum-ata-laksh.eps}](img14.png)
![\includegraphics[width=3.2in]{figures/cksum-struct.eps}](img15.png)
![\includegraphics[width=3.2in]{figures/age-ata.eps}](img27.png)
![\includegraphics[width=3.3in]{figures/age-fc-1.eps}](img28.png)
![\includegraphics[width=3.3in]{figures/age-fc-2.eps}](img29.png)

![\includegraphics[width=3.3in]{figures/size-ata.eps}](img37.png)
![\includegraphics[width=3.3in]{figures/size-fc.eps}](img38.png)
![\includegraphics[width=3.3in]{figures/cpercdisk-ata.eps}](img40.png)
![\includegraphics[width=3.3in]{figures/cpercdisk-fc.eps}](img41.png)
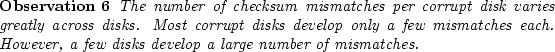
![\includegraphics[width=3.3in]{figures/spatial-ata.eps}](img51.png)
![\includegraphics[width=3.3in]{figures/spatial-fc.eps}](img52.png)
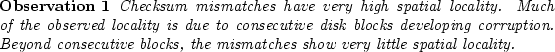
![\includegraphics[width=3.3in]{figures/inter-arrival-ata.eps}](img62.png)
![\includegraphics[width=3.3in]{figures/inter-arrival-fc.eps}](img63.png)
![\includegraphics[width=.8\columnwidth]{figures/autocor.eps}](img71.png)
![\includegraphics[width=3.3in]{figures/request.eps}](img80.png)
![\includegraphics[width=3.3in]{figures/lw-ata.eps}](img83.png)
![\includegraphics[width=3.3in]{figures/lw-fc.eps}](img84.png)
![\includegraphics[width=3.3in]{figures/pi-ata.eps}](img86.png)
![\includegraphics[width=3.3in]{figures/pi-fc.eps}](img87.png)
![\includegraphics[width=3.2in]{figures/e1blocknums.eps}](img88.png)