FAST '05 Paper
[FAST '05 Technical Program]
TAPER: Tiered Approach for
Eliminating Redundancy in Replica Synchronization
Navendu Jain , Mike Dahlin , Mike Dahlin , and Renu Tewari , and Renu Tewari
 Department of Computer Sciences, University
of Texas at Austin, Austin, TX, 78712 Department of Computer Sciences, University
of Texas at Austin, Austin, TX, 78712
 IBM Almaden Research Center, 650 Harry
Road, San Jose, CA, 95111 IBM Almaden Research Center, 650 Harry
Road, San Jose, CA, 95111
{nav,dahlin}@cs.utexas.edu, tewarir@us.ibm.com
Abstract
We present TAPER, a scalable data replication protocol that
synchronizes a large collection of data across multiple
geographically distributed replica locations. TAPER can be applied to
a broad range of systems, such as software distribution mirrors,
content distribution networks, backup and recovery, and federated file
systems. TAPER is designed to be bandwidth efficient, scalable and
content-based, and it does not require prior knowledge of the replica
state. To achieve these properties, TAPER provides: i) four
pluggable redundancy elimination phases that balance the trade-off
between bandwidth savings and computation overheads, ii) a
hierarchical hash tree based directory pruning phase that
quickly
matches identical data from the granularity of directory trees to
individual files, iii) a content-based similarity detection technique
using Bloom filters to identify similar files, and iv) a
combination of
coarse-grained chunk matching with finer-grained block matches to
achieve bandwidth efficiency.
Through extensive experiments
on various datasets, we observe that in comparison with rsync, a
widely-used directory synchronization tool, TAPER reduces bandwidth
by 15% to 71%, performs faster matching, and scales
to a larger number of replicas.
1 Introduction
In this paper we describe TAPER, a redundancy elimination protocol for
replica
synchronization. Our motivation for TAPER arose from building a
federated file system using NFSv4 servers, each sharing
a common system-wide namespace [25].
In this system, data is
replicated from a master server to a collection of servers, updated
at the master, periodically synchronized to the other servers, and
read from any server via NFSv4 clients. Synchronization in this
environment requires a protocol that minimizes both network bandwidth
consumption and end-host overheads. Numerous
applications have similar requirements: they require replicating and
synchronizing a large collection of data across multiple sites,
possibly over low-bandwidth links. For example, software distribution
mirror sites, synchronizing personal systems with a remote server,
backup and restore systems, versioning systems, content distribution
networks (CDN), and federated file systems all rely on synchronizing
the
current data at the source with older versions of the data at remote
target sites and could make use of TAPER.
Unfortunately, existing approaches do not suit such environments. On
one
hand, protocols such as delta compression (e.g., vcdiff [14])
and snapshot differencing (e.g., WAFL [11]) can efficiently
update one site from another, but they require a priori
knowledge of which versions are stored at each site and what changes
occurred between the versions. But, our environment requires a
universal data synchronization protocol that interoperates with
multi-vendor NFS implementations on different operating systems
without any knowledge of their internal state to determine the version
of the data at the replica. On the other hand, hash-based differential
compression protocols such
as rsync [2] and LBFS [20] do not require a
priori knowledge of replica state, but they are inefficient. For
example, rsync relies on path names to identify similar files and
therefore transfers large amounts of data when a
file or directory is renamed or copied, and LBFS's single-granularity
chunking compromises efficiency (a) by transferring extra metadata when
redundancy spanning
multiple chunks exists and (b) by missing similarity on granularities
smaller than the chunk size.
The TAPER design focuses on providing four key properties in order to
provide speed, scalability, bandwidth efficiency, and computational
efficiency:
- P1: Low, re-usable computation at the source
- P2: Fast matching at the target
- P3: Find maximal common data between the source and the
target
- P4: Minimize total metadata exchanged
P1 is necessary for a scalable solution that can simultaneously
synchronize multiple targets with a source. Similarly, P2 is
necessary to reduce the matching time and, therefore, the total
response time for synchronization. To support P2, the matching at the
target should be based on indexing to identify the matching components
in O(1) time. The last two, P3 and P4, are both indicators of
bandwidth efficiency as they determine the total amount of data and the
total metadata information (hashes etc.) that are
transferred. Balancing P3 and P4 is the key requirement in order to
minimize the metadata overhead for the data transfer savings. Observe
that in realizing P3, the source and target should find common data
across all files and not just compare file pairs based on name.
To provide all of these properties, TAPER is a multi-phase,
hierarchical protocol. Each phase operates over decreasing data
granularity, starting with directories and files, then large chunks,
then smaller blocks, and finally bytes. The phases of TAPER balance the
bandwidth efficiency of smaller-size matching with the reduced
computational overhead of lesser unmatched data. The first phase of
TAPER eliminates all common files and quickly prunes directories using
a content-based hierarchical hash tree data structure. The
next phase eliminates all common content-defined chunks (CDC) across
all files. The third phase operates on blocks within the remaining
unmatched chunks by applying a similarity detection technique based on
Bloom filters. Finally, the matched and unmatched blocks remaining at
the source are further delta encoded to eliminate common bytes.
Our main contributions in this paper are: i) design of a new
hierarchical hash tree data structure for fast pruning of directory
trees, ii) design and analysis of a similarity detection technique
using CDC and Bloom filters that compactly represent the content of a
file,
iii) design of a combined CDC and sliding block technique for
both coarse-grained and fine-grained matching, iv) integrating and
implementing all
the above techniques in TAPER, a multi-phase, multi-grain protocol,
that is engineered as pluggable units. The phases of TAPER are
pluggable in that each phase uses a different mechanism corresponding
to data granularity, and a phase can be dropped all together to trade
bandwidth savings for computation costs. And, v) a complete prototype
implementation and performance evaluation of our system.
Through extensive experiments
on various datasets, we observe that TAPER reduces
bandwidth by 15% to 71% over rsync
for different workloads.
The rest of the paper is organized as follows. Section 2
provides an overview of the working of sliding block and CDC. These
operations form the basis of both the second and third phases that lie
at the core of TAPER.
The overall TAPER
protocol is described in detail in Section 3.
Similarity
detection using CDC and Bloom filters is described and analyzed in
Section 4. Section 5
evaluates and compares
TAPER for different workloads. Finally, Section 6
covers
related work and we conclude with Section 7.
2 Background
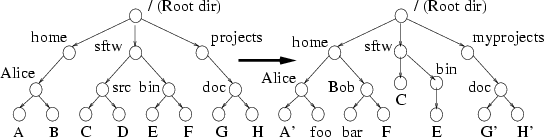
Figure 1: Directory Tree
Synchronization Problem: The source tree
is shown on the left and the target tree with multiple updates,
additions, and renames, is on the right.
In synchronizing a directory tree between a source and target
(Figure 1), any approach should
efficiently handle all
the common update operations on file systems. These include: i) adding,
deleting, or modifying files and directories, ii) moving files or
directories to other parts of the tree, iii) renaming files and
directories, and iv) archiving a large collection of files and
directories into a single file (e.g., tar, lib).
Although numerous tools and utilities exist for directory
synchronization with no data versioning information, the underlying
techniques are either based on matching: i) block hashes or ii) hashes
of content-defined chunks. We find that sliding block hashes
(Section 2.1) are well suited to
relatively fine-grained matching between similar files, and that CDC
matching (Section 2.2) is
suitable for more coarse-grained, global matching
across all files.
|
|
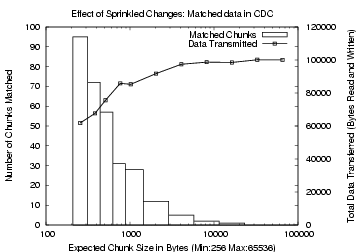
Figure 2: Effect of Sprinkled
Changes in CDC. The x-axis
is the expected chunk size. The left y-axis, used for the bar graphs,
shows the number of matching chunks. The right y-axis, for the line
plot, shows the total data transferred
.
|
|
|
|
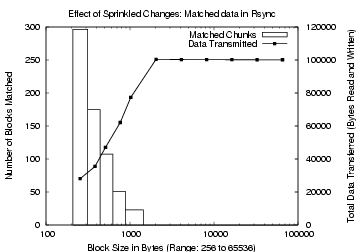
Figure 3: Effect of Sprinkled
Changes in Rsync. The
x-axis is the fixed block size. The left y-axis, used for the bar
graphs, shows the number of matching blocks. The right y-axis, for the
line plot, shows the total data transferred.
|
|
|
2.1 Fixed and Sliding Blocks
In block-based protocols, a fixed-block approach computes the
signature (e.g., SHA-1, MD5, or MD4 hash) of a fixed-size block at both
the source and target and simply indexes the signatures for a quick
match.
Fixed-block matching performs poorly because small modifications change
all
subsequent block boundaries in a file and eliminate any remaining
matches. Instead, a
sliding-block approach is used in protocols like rsync for a better
match. Here, the target, T, divides a file f into non-overlapping,
contiguous, fixed-size blocks and sends its signatures, 4-byte MD4
along with a 2-byte rolling checksum (rsync's implementation uses full
16 byte MD4
and 4 byte rolling checksums per-block for large files), to the source
S. If an existing file
at S, say f¢, has the same name as f,
each block signature of
f is compared with a sliding-block signature of every overlapping
fixed-size block in f¢.
There are several variants
of the basic sliding-block approach, which we discuss in
Section 6, but all of them compute a
separate
multi-byte checksum for each byte of data to be transferred. Because
this checksum information is large compared to the
data being stored, it would be too costly to store all checksums for
all
offsets of all files in a system, so these systems must do matching on
a finer (e.g., per-file) granularity. As a result, these systems have
three fundamental problems. First, matching requires knowing which file
f¢ at the
source should be matched with the file f at the target. Rsync simply
relies on file names being the same. This approach makes rsync
vulnerable to name
changes (i.e., a rename or a move of a directory tree will result in
no matches, violating property P3). Second, scalability with the number
of replicas is limited because the source machine recomputes the
sliding block match for every file and for
every target machine and
cannot re-use any hash computation (property P1). Finally, the
matching time is high as there is no indexing support for the
hashes: to determine if a block matches takes time of the order of
number of bytes in a file as
the rolling hash has to be computed over the entire file until a match
occurs (property P2). Observe that rsync [2] thus violates
properties P1, P2, and P3. Although rsync is a widely used protocol
for synchronizing a single client and server, it is not designed for
large scale replica synchronization.
To highlight the problem of name-based matching in rsync, consider,
for example, the source directory of GNU Emacs-20.7 consisting of
2086 files with total size of 54.67 MB.
Suppose we rename only the top level
sub-directories in Emacs-20.7 (or move them to another part of the
parent
tree). Although no data has changed, rsync would have sent the entire
54.67 MB of data with an additional 41.04 KB of hash metadata (using
the default block size of 700 bytes), across the network. In contrast,
as we describe in Section 3.1.1, TAPER
alleviates this
problem by performing content-based pruning using a hierarchical hash
tree.
2.2 Content-defined Chunks
Content-defined chunking balances the fast-matching of a
fixed-block approach with the finer data matching ability of
sliding-blocks. CDC has been used in LBFS [20],
Venti [21] and other systems
that we discuss in Section 6. A chunk is a
variable-sized
block whose boundaries are determined by its Rabin
fingerprint matching a pre-determined marker value [22]. The
number of bits in the Rabin fingerprint that are used to match the
marker determine the expected chunk size. For example, given a marker
0x78 and an expected chunk size of 2k, a rolling
(overlapping
sequence) 48-byte fingerprint is computed. If the lower k bits of
the fingerprint equal 0x78, a new chunk boundary is set. Since
the chunk boundaries are content-based, a file modification should
affect only neighboring chunks and not the entire file.
For matching, the SHA-1 hash of the chunk is used. Matching a chunk
using CDC
is a simple hash table lookup.
Clearly, the expected chunk size is critical to the
performance of CDC and depends on the degree of file
similarity and the locations of the file modifications. The chunk
size is a trade-off between the degree of matching and the size of the
metadata (hash values). Larger chunks reduce the size of metadata but
also reduce the number of matches. Thus, for any given chunk size, the
CDC approach violates properties P3, P4, or both.
Furthermore, as minor
modifications can affect neighboring chunks, changes sprinkled across a
file can result in few
matching chunks. The expected chunk size is manually
set in LBFS (8 KB default). Similarly, the fixed block size is
manually selected in rsync (700 byte default).
To illustrate the effect of small changes randomly distributed in a
file, consider,
for example, a file (say `bar') with 100 KB of data that is updated
with
100 changes of 10 bytes each (i.e., a 1% change).
Figures 2 and 3
show the variations
due to sprinkled changes in the matched data for CDC and rsync,
respectively. Observe that while rsync finds more matching data than
CDC for small block sizes, CDC performs better for large chunk
sizes. For a block and expected chunk size of 768 bytes, rsync
matched 51 blocks, transmitting a total of 62 KB, while CDC
matched 31 chunks, transmitting a total of 86 KB. For a larger
block size of 2 KB, however, rsync found no matches, while CDC
matched 12 chunks and transmitted 91 KB. In designing TAPER, we use
this observation to apply CDC in the earlier phase with relatively
larger chunk sizes.
3 TAPER Algorithm
In this section, we first present the overall architecture of the
TAPER protocol
and then describe each of the four TAPER phases in detail.
3.1 TAPER Protocol Overview
TAPER is a directory tree synchronization protocol between a source and
a target node that aims at minimizing the transmission of any common
data that already exists at the target. The TAPER protocol does not
assume any knowledge of the state or the version of the data at the
target. It, therefore, builds on hash-based techniques for data
synchronization.
In general, for any hash-based synchronization protocol, the smaller
the matching granularity the better the match and lower the number of
bytes transfered. However, fine-grained matching increases the metadata
transfer (hash values per block) and the computation overhead. While
systems with low bandwidth networks will optimize on the total data
transferred, those with slower servers will optimize the computation
overhead.
The intuition behind TAPER is to work in phases (Figure 4) where each phase moves from a larger to a
finer matching granularity. The protocol works in four phases: starting
from a directory tree, moving on to large chunks, then to smaller
blocks, and finally to bytes. Each phase in TAPER uses the best
matching technique for that size, does the necessary transformations,
and determines the set of data over which the matches occur.
Specifically, the first two phases perform coarse grained matching at
the level of directory trees and large CDC chunks (4 KB expected
chunk size). Since the initial matching is performed at a high
granularity, the corresponding hash information constitutes only a
small fraction of the total data. The SHA-1 hashes computed in the
first two phases can therefore be pre-computed once and stored in a
global and persistent database at the source. The
global database maximizes matching by allowing any directory,
file,
or chunk that the source wants to transmit to be matched against any
directory, file, or chunk that the target stores. And the
persistent database enhances computational efficiency by allowing
the
source to re-use hash computations across multiple targets.
Conversely, the last two phases perform matching at the level of
smaller blocks (e.g., 700 bytes), so precomputing and storing all
hashes of all small blocks would be expensive. Instead, these phases
use local matching in which they identify similar files or
blocks and compute and temporarily store summary metadata
about
the specific files or blocks currently being examined. A key building
block for these phases is efficient similarity detection,
which
we assume as a primitive in this section and discuss in detail in
Section 4.
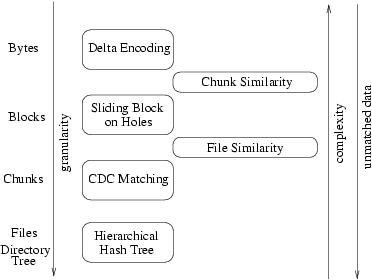
Figure 4: The building blocks of TAPER
3.1.1 Directory Matching
The first phase, directory matching, eliminates identical portions
of the
directory tree that are common in content and structure (but may have
different names) between the source and the target. We define a hierarchical
hash tree (HHT) for this
purpose to quickly find all the exact matching subtrees progressing
down from the largest to the smallest directory match and finally
matching identical individual files.
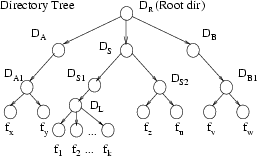
Figure 5: Phase I: Hierarchical Hash Tree
|
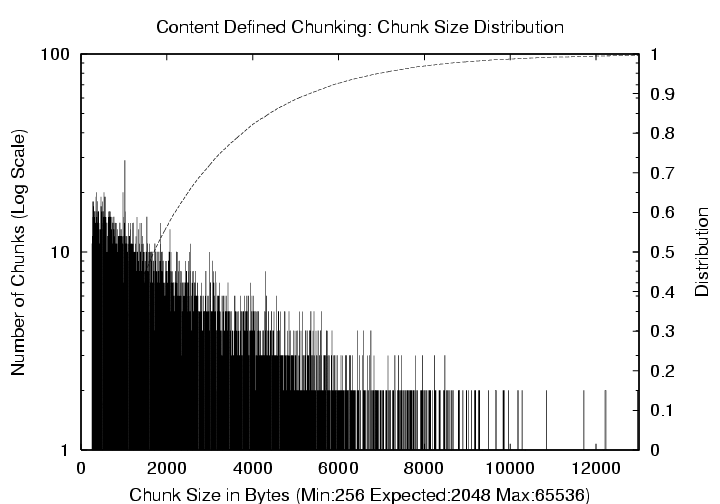
Figure 6: Emacs-20.7 CDC
Distribution (Mean = 2 KB, Max = 64 KB). The
left y-axis (log scale) corresponds to the histogram of chunk sizes,
and the right y-axis shows the cumulative distribution.
|
|
|
|
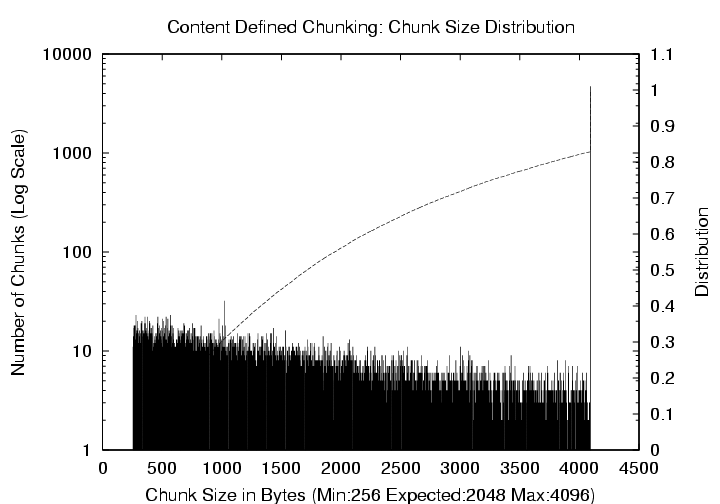
Figure 7: Emacs-20.7 CDC
Distribution (Mean = 2KB, Max = 4 KB). The
left y-axis (log scale) corresponds to the histogram of chunk sizes,
and the right y-axis shows the cumulative distribution.
|
|
|
The HHT representation encodes the directory structure and contents of
a directory tree as a list of hash values for every node in the
tree. The nodes consist of the root of the directory tree, all the
internal sub-directories, leaf directories, and finally all the
files. The HHT structure is recursively computed as follows. First, the
hash
value of a file node fi is obtained using a standard
cryptographic
hash algorithm (SHA-1) of the contents
of the file. Second, for a leaf directory DL, the hash value
h(DL) is
the hash of all the k constituent file hashes, i.e., h(DL) =
h(h(f1)h(f2) ... h(fk)). Note that the
order of concatenating hashes of files within the same directory
is based on the hash values and not on the file names.
Third, for a non-leaf sub-directory, the hash value
captures not only the content as in Merkle trees but also the structure
of the tree. As
illustrated in Figure 5, the hash of a
sub-directory DS
is computed by an in-order traversal of all its immediate
children. For example, if DS = { DS1, DS2}
then
| h(DS) =
h(h(DN) h( DS1) h(UP) h(DN) h(DS2) h(UP)) |
|
where "UP" and "DN" are two literals representing the traversal of the
up and down links in the tree respectively. Finally, the hash of the
root node, DR,
of the directory tree is computed similar to that of a subtree defined
above. The HHT algorithm, thus, outputs a list of the hash values of
all the nodes,
in the directory tree i.e., h(DR), h(DA), h(DS),
¼, h(DL), ¼, h(f1) ¼ .
Note that our HHT technique provides a hierarchical encoding of both
the file content
and the directory structure. This proves beneficial in eliminating
directory trees identical in content and structure at the highest
level.
The target, in turn, computes the HHT hash values of its
directory tree and stores each element in a hash table. Each element of
the HHT sent by the source-starting at the root node of the directory
tree and if necessary progressing downward to the
file nodes-is used to index into the
target's hash table to see if the node matches any node at the
target. Thus, HHT finds the maximal common directory match and enables
fast
directory pruning since a match at any node implies that all the
descendant nodes match as well. For example, if the root hash values
match,
then no further matching is done as the trees are identical in both
content and structure. At the end of
this phase, all exactly matching directory trees and files would have
been pruned.
To illustrate the advantage of HHT, consider, for example, a rename
update of the root directory of Linux Kernel 2.4.26 source tree. Even
though no content was changed, rsync found no matching data and sent
the entire tree of size 161.7 MB with an additional 1.03 MB of metadata
(using the default block-size of 700 bytes). In contrast, the HHT phase
of TAPER sent 291 KB of the HHT metadata and determined, after a single
hash match of the root node, that the entire data was identical.
The main advantages of using HHT for directory pruning are that it can:
i) quickly (in O(1) time) find the maximal exact match, ii) handle
exact matches from the entire tree to individual files,
iii) match both structure and content, and iv) handle file or directory
renames and moves.
3.1.2 Matching Chunks
Once all the common files and directories have been eliminated, we are
left with a set of unmatched files at the source and the target. In
Phase II, to
capture the data commonality across all files and further
reduce
the unmatched data, we rely on content-defined chunking (which we
discussed in Section 2). During this
phase, the target sends the SHA-1 hash
values of the unique (to remove local redundancy)
CDCs of all the remaining files to the source.
Since CDC hashes can be indexed for fast matching, the source can
quickly eliminate all the matching chunks across all the files between
the source and target. The source stores the CDC hashes locally for
re-use when synchronizing with multiple targets.
When using CDCs, two parameters- the expected chunk size and the
maximum chunk size- have to be selected for a given workload.
LBFS [20] used an expected
chunk size of 8 KB with a
maximum of 64 KB. The chunk sizes, however, could have a large
variance around the mean. Figure 6 shows
the frequency
and cumulative distribution of chunk sizes for the Emacs-20.7 source
tree using an expected chunk size value of 2 KB with no limitation
on the chunk size except for the absolute maximum of 64 KB. As can be
seen from the figure, the chunk sizes have a large variance, ranging
from 256 bytes to 12 KB with a relatively long tail.
The maximum chunk size limits this variance by forcing a chunk to be
created if the size exceeds the maximum value. However, a forced split
at
fixed size values makes the algorithm behave more like fixed-size
block matching with poor resilience to updates. Figure 7
shows the distribution of chunk sizes for the same workload and
expected chunk size value of 2 KB with a maximum value now set to
4 KB. Approximately 17% of the chunks were created due to this
limitation.
Moreover, as an update affects the neighboring chunks, CDCs are not
suited for fine-grained matches when there are small-sized updates
sprinkled throughout the data. As we observed in
Figures 2 and 3
in
Section 2, CDC performed better than
sliding-block for
larger sized chunks, while rsync was better for finer-grained matches.
We, therefore, use a relatively large expected chunk size (4 KB) in
this phase to do fast, coarse-grained matching of data across all the
remaining
files. At the end of the chunk
matching phase, the source has a set of files each with a sequence of
matched and unmatched regions. In the next phase, doing finer-grained
block matches, we try to reduce the size of these unmatched regions.
3.1.3 Matching Blocks
After the completion of the second phase, each file at the source would
be in the form of a
series of matched and unmatched regions. The contiguous unmatched
chunks lying in-between two matched chunks of the same file are merged
together and are called holes. To reduce the size of the
holes,
in this phase, we perform finer-grained block matching. The
sliding-block match, however, can be applied only to a pair
of
files. We, therefore, need to determine the constituent files to
match a pair of holes, i.e., we need to determine which pair of files
at the source and target are similar. The technique we use for
similarity detection is needed in multiple phases, hence, we discuss
it in detail in Section 4. Once we identify
the pair of similar files to
compare, block matching is applied to the holes of the file at the
source. We split the unmatched holes of a file, f, at the source
using relatively smaller fixed-size blocks (700 bytes) and send the
block signatures (Rabin fingerprint for weak rolling checksum; SHA-1
for strong checksum) to the target. At the target, a
sliding-block match is used to compare against the holes in the
corresponding file. The target then requests the set of unmatched
blocks from the source.
To enable a finer-grained match, in this phase, the matching size of
700 bytes
is selected to be a fraction of the expected chunk size of
4 KB. The extra cost of smaller blocks is offset by the fact that we
have much less data (holes instead of files) to work with.
3.1.4 Matching Bytes
This final phase further reduces the bytes to be sent. After the
third phase, the source has a set of unmatched blocks remaining. The
source also has the set of matched chunks, blocks and files that
matched in the first three phases. To further reduce the bytes to be
sent, the blocks in the unmatched set are delta encoded with
respect to a similar block in the matched set. The target can then
reconstruct the block by applying the delta-bytes to the matched
block. Observe that unlike redundancy elimination techniques for
storage, the source does not have the data at the target. To
determine which matched and unmatched blocks are similar, we apply the
similarity detection technique at the source.
Finally, the remaining unmatched blocks and the delta-bytes are
further compressed using standard compression algorithms (e.g., gzip)
and sent to the target. The data at the target is validated in the
end by sending an additional checksum per file to avoid any
inconsistencies.
3.1.5 Discussion
In essence, TAPER combines
the faster matching of content-defined chunks and the finer matching
of the sliding block approach. CDC helps in finding common data across
all files, while sliding-block can find small random changes
between a pair of files. Some of the issues in implementing TAPER
require further discussion:
- Phased refinement:
The multiple phases of TAPER result in better differential compression.
By
using a coarse granularity for a larger dataset we reduce the
metadata overhead. Since the dataset size reduces in each phase, it
balances the computation and metadata overhead of finer granularity
matching. The
TAPER phases are not just recursive application of the same algorithm
to smaller block sizes. Instead, they use the best approach for a
particular size.
- Re-using Hash computation: Unlike rsync where the source
does the sliding-block match, TAPER
stores the hash values at the source both in the directory matching and
the chunk matching phase. These values need not be recomputed
for different targets, thereby, increasing the scalability of
TAPER. The hash values are computed either when the source file system
is
quiesced or over a consistent copy of the file system, and are stored
in a
local database.
- Pluggable: The TAPER phases are pluggable in that some can
be dropped if the desired level of data reduction has been achieved.
For example, Phase I can be directly combined with Phase III and
similarity detection giving us an rsync++. Another possibility is just
dropping phases III and IV.
- Round-trip latency:
Each phase of TAPER requires a metadata exchange between the server
and the target corresponding to one logical round-trip. This
additional round-trip latency per phase is balanced by the fact that
amount of data and metadata transferred is sufficiently reduced.
- Hash collisions:
In any hash-based differential compression technique there is the
extremely low but non-zero probability of a hash
collision [10]. In systems
that use hash-based
techniques to compress local data, a collision may corrupt the source
file system. TAPER is used for replica synchronization and hence only
affects the target data. Secondly, data is
validated by a second cryptographic checksum over the entire file. The
probability of two
hash collisions over the same data is quadratically lower and we
ignore that possibility.
The recent attack on the SHA-1 hash function [26] raises the challenge of an attacker
deliberately creating two files with the same content [1].
This attack can be addressed by prepending a secret, known only to the
root at the source and target,
to each chunk before computing the hash value.
|
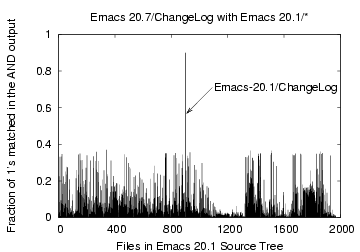
Figure 8: Bloom filter Comparison
of the file 'Emacs-20.7/ChangeLog' with files 'Emacs-20.1/
|
|
|
|
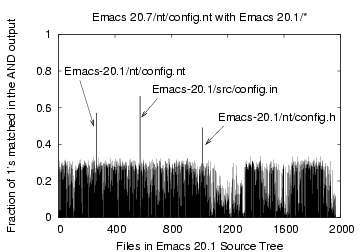
Figure 9: Bloom filter Comparison
of the file 'Emacs-20.7/nt/config.nt' with files 'Emacs-20.1/*'
|
|
|
|
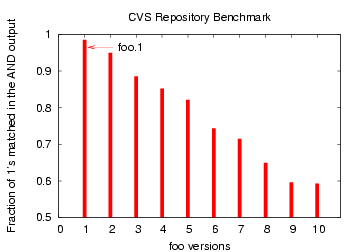
Figure 10: Bloom filter Comparison
of file `foo' with later versions `foo.1', `foo.2', ... `foo.10'
|
|
|
4 Similarity Detection
As we discussed in Section 3, the last
two phases of the
TAPER protocol rely on a mechanism for similarity detection. For block
and byte matching, TAPER needs to determine which two files or chunks
are similar. Similarity detection for files has been extensively
studied in the WWW domain and relies on shingling [22] and
super fingerprints discussed later in Section 4.3.
In TAPER, we explore the application of Bloom filters for file
similarity detection. Bloom filters compactly represent a set of
elements using a finite number of bits and are used to answer
approximate set membership queries. Given that Bloom filters compactly
represent a set, they can also be
used to approximately match two sets. Bloom filters,
however, cannot be used for exact matching as they have a finite
false-match probability, but they are naturally suited for similarity
matching. We first give a brief overview of Bloom filters, and later
present and analyze the similarity detection technique.
4.1 Bloom Filters Overview
A Bloom filter is a space-efficient representation of a set. Given
a set U, the Bloom filter of U is implemented as an array of m
bits, initialized to 0 [4].
Each element u (u Î U) of the set is
hashed
using k independent hash functions h1,¼,hk.
Each hash
function hi(u) for 1 £
i £ k returns a value between 1
and
m then
when an element is added to the set, it
sets k bits, each bit corresponding to a hash function output, in the
Bloom
filter array to 1. If a bit was already set it stays 1. For set
membership queries, Bloom filters may yield a false positive,
where
it may appear that an element v is in U even though it is not.
From the analysis in the survey paper by Broder and Mitzenmacher [8], given n = |U| and the Bloom
filter size m, the optimal value of k that minimizes the false
positive probability, pk, where p denotes that probability
that a
given bit is set in the Bloom filter, is k = [m/n] ln2.
4.2 Bloom Filters for
Similarity Testing
Observe that we can view each file to be a set in
Bloom filter parlance whose elements are the CDCs that it is composed
of. Files with
the same set of CDCs have the same Bloom filter
representation. Correspondingly, files that are similar have a large
number of 1s common among their Bloom filters.
For multisets, we make each
CDC unique before Bloom filter generation to differentiate multiple
copies of the same CDC.
This is achieved by attaching an index value of each CDC chunk
to its SHA-1 hash. The index ranges from 1 to lnr, where r is the
multiplicity of the given chunk in the file.
For finding similar files, we compare the Bloom filter of a given file
at the
source with that of all the files at the replica. The file sharing the
highest number of 1's (bit-wise AND) with the source file and above a
certain threshold (say 70%) is marked as the matching file. In this
case, the bit wise AND can also be perceived as the dot
product of the two bit vectors. If the 1 bits in the Bloom filter of a
file are a complete
subset of that of another filter then it is highly probable that the
file is included in the other.
Bloom filter when
applied to similarity detection have several advantages. First, the
compactness of Bloom filters is very attractive for remote replication
(storage and transmission)
systems where we want to minimize the metadata overheads. Second,
Bloom filters enable fast comparison as matching is a bitwise-AND
operation. Third, since Bloom filters are a complete representation of
a set rather than a deterministic sample (e.g., shingling), they can
determine inclusions effectively e.g., tar files and libraries.
Finally, as they have a low metadata
overhead they could be combined further with either sliding block or
CDC for narrowing the match space.
To demonstrate the effectiveness of Bloom filters for similarity
detection, consider, for example, the file ChangeLog in the
Emacs-20.7 source distribution which we compare against all the
remaining 1967 files in the Emacs-20.1 source tree. 119 identical
files out of a total 2086 files were removed in the HHT phase.
The CDCs
of the files were computed using an expected and maximum chunk size of
1 KB
and 2 KB respectively.
Figure 8 shows
that the corresponding ChangeLog file in the Emacs-20.1
tree matched the most with about 90% of the bits matching.
As another example, consider the file nt/config.nt in
Emacs-20.7 (Figure 9) which we compare
against the files of
Emacs-20.1. Surprisingly, the file that matched most was-
src/config.in-a file with a different name in a different
directory tree. The CDC expected and maximum chunk sizes were 512 bytes
and 1 KB respectively.
Figure 9 shows that while the file with
the
same name nt/config.nt matched in 57% of the bits, the file
src/config.in matched in 66%. We further verified this by
computing
the corresponding diff output of 1481 and 1172 bytes,
respectively. This experiment further emphasizes the need for
content-based similarity detection.
To further illustrate that Bloom filters can differentiate between
multiple similar files, we extracted a technical documentation
file `foo' (say)
(of size 175 KB) incrementally from a CVS archive, generating 10
different versions,
with `foo' being the original, `foo.1' being the first version (with
a change of 4154 bytes from `foo') and `foo.10' being
the last. The CDC chunk sizes were chosen as in the ChangeLog
file example above.
As shown in Figure 10, the Bloom filter
for
'foo' matched the most (98%) with the closest version `foo.1'
and the least (58%) with the latest version `foo.10'.
|
|
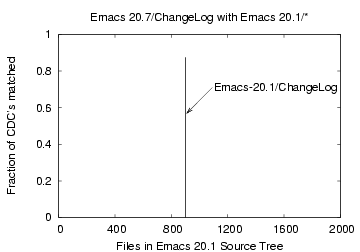
Figure 11: CDC comparison of the
file 'Emacs-20.7/ChangeLog' with files 'Emacs-20.1/*'
|
|
|
|
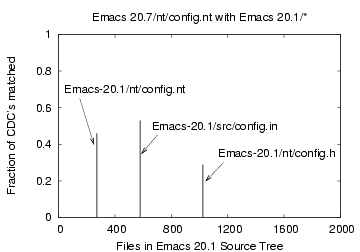
Figure 12: CDC comparison of the
file 'Emacs-20.7/nt/config.nt' with files 'Emacs-20.1/*'
|
|
|
|
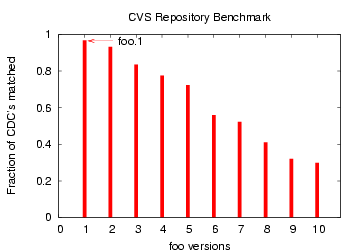
Figure 13: CDC Comparison of file
`foo' with later versions `foo.1', `foo.2', ... `foo.10'
|
|
|
The main consideration when using Bloom filters for similarity
detection is the false match probability of the above algorithm as a
function of similarity between the source and a candidate file.
Extending the
analysis for membership testing [4]
to similarity
detection, we proceed to determine the expected number of inferred
matches between the two sets. Let A and B be the two sets being
compared for similarity. Let m denote the number of bits (size) in
the Bloom filter. For simplicity, assume that both sets have the same
number of elements. Let n denote the number of elements in both sets
A and B i.e., |A|
= |B| = n. As
before, k denotes the number
of hash functions. The probability that a bit is set by a hash
function hi for 1 £
i £ k is [1/m]. A bit can be set
by any of the k hash functions for each of the n elements.
Therefore, the probability that a bit is not set by any hash function
for any element is (1 - [1/m])nk.
Thus, the
probability, p, that a given bit is set in the Bloom filter of A is
given by:
| p = |
æ
è
|
1 -
|
æ
è
|
1 -
|
1
m
|
|
ö
ø
|
nk
|
|
ö
ø
|
» 1 - e-[nk/m] |
|
(1) |
For an element to be considered a member of the set, all the
corresponding k bits should be set. Thus, the probability of a false
match, i.e., an outside element is inferred as being in set A, is pk.
Let C denote the intersection of sets A and B and c denote its
cardinality, i.e., C = A ÇB
and |C| = c.
For similarity comparison, let us take each element in set B and
check if it belongs to the Bloom filter of the given set A. We should
find
that the c common elements will definitely match and a few of
the other (n-c) may also match due to the
false match probability. By Linearity of Expectation, the expected
number of elements of B inferred to have matched with A is
| E[# of
inferred matches]
= (c) + (n-c) pk |
|
To minimize the false matches, this expected number should be as close
to c as possible. For that (n-c)pk
should be close to 0, i.e.,
pk should approach 0. This happens to be the same as
minimizing the probability of a false positive. Expanding p and under
asymptotic analysis, it reduces to minimizing (1 -e-[nk/m])k. Using the same
analysis for minimizing the false
positive rate [8], the
minima obtained after differentiation is
when k = [m/n] ln2 . Thus, the expected number of inferred
matches for this
value of k becomes
| E[# of
inferred matches]
= c + (n-c) (0.6185)[m/n]
|
|
Thus, the expected number of bits set corresponding to inferred matches
is
| E[# of
matched bits] = m |
é
ë
|
1 -
|
æ
è
|
1- |
1
m
|
|
ö
ø
|
k(c +
(n-c) (0.6185)[m/n])
|
|
ù
û
|
|
|
Under the assumption of perfectly random hash functions,
the expected number of total bits set in the Bloom filter of the source
set A, is mp. The ratio, then, of the expected number of matched bits
corresponding to inferred matches in A ÇB
to the expected total number of bits set in the Bloom filter of A is:
|
E[# of
matched bits]
E[# total bits set]
|
= |
|
æ
è
|
1 - e-[k/m](c
+ (n-c) (0.6185)[m/n]) |
ö
ø
|
|
|
|
Observe that this ratio equals 1 when all the elements match, i.e.,
c = n. If there are no matching elements, i.e., c = 0, the ratio =
2(1 - (0.5)(0.6185)[m/n]).
For m = n, this evaluates to 0.6973, i.e.,
69% of matching bits may be false. For larger values, m = 2n, 4n,8n,
10n, 11n, the corresponding ratios are 0.4658, 0.1929, 0.0295,
0.0113, 0.0070 respectively. Thus, for m = 11n, on an average, less
than
1% of the bits set may match incorrectly. The expected ratio of
matching bits is highly correlated to the expected ratio of matching
elements. Thus, if a large fraction of the bits match, then it's
highly likely that a large fraction of the elements are common.
Although the above analysis was done based on expected values, we show
in an extended technical report [13] that under the assumption that the
difference between p and
(1 - e-[nk/m])
is very small, the actual number of
matched bits is highly concentrated around the expected
number of matched bits with small variance [18].
Given that the number of bits in the Bloom filter should be larger
than the number of elements in the set we need large filters for
large files. One approach is to select a new filter size when the
file size doubles and only compare the files represented with the same
filter size.
To support subset matching, however, the filter
size for all the files should be identical and therefore all files need
to have a filter size
equal to size required for the largest file.
4.2.2 Size of the Bloom Filter
As discussed in the analysis, the fraction of bits
matching incorrectly depends on the size of the Bloom filter. For a
97% accurate match, the number of bits in the Bloom filter should be
8x the number of elements (chunks) in the set (file). For a file of
size 128 KB, an expected and maximum chunk size of 4 KB and 64 KB,
respectively
results in around 32 chunks. The Bloom filter is set to be 8x this
value i.e., 256 bits.
For small files, we can set the expected chunk size to 256 bytes.
Therefore, the Bloom filter size is set to 8x the expected number of
chunks (32 for 8 KB file) i.e., 256 bits, which is a 0.39% and 0.02%
overhead for file size of 8 KB and 128 KB, respectively.
4.3 Comparison with Shingling
Previous work on file similarity has mostly been based on
shingling or super fingerprints. Using this method, for each object,
all the k consecutive words of a file (called k-shingles) are
hashed using Rabin fingerprint [22]
to create a set of
fingerprints (also called features or pre-images). These fingerprints
are then sampled to compute a super-fingerprint of the file. Many
variants have been proposed that use different techniques on how the
shingle fingerprints are sampled (min-hashing, Modm, Mins,
etc.)
and matched [7,6,5].
While Modm selects all fingerprints whose
value modulo m is zero; Mins selects the set of s
fingerprints
with the smallest value. The min-hashing approach further refines the
sampling to be the min values of say 84 random min-wise independent
permutations (or hashes) of the set of all shingle fingerprints. This
results in a fixed size sample of 84 fingerprints that is the
resulting feature vector. To further simplify matching, these 84
fingerprints can be grouped as 6 "super-shingles" by concatenating
14 adjacent fingerprints [9].
In REBL [15] these
are called super-fingerprints. A pair of objects are then considered
similar if either all or a large fraction of the values in the
super-fingerprints match.
Our Bloom filter based similarity detection differs from the shingling
technique in several ways. It should be noted, however, that the
variants of shingling discussed above improve upon the original
approach and we provide a comparison of our
technique with these variants wherever applicable. First, shingling
(Modm, Mins) computes file similarity using the
intersection of the two feature sets. In our approach, it requires
only the bit-wise AND of the two Bloom filters (e.g., two 128 bit
vectors). Next, shingling has a higher computational overhead
as it first segments the file into k-word shingles (k=5 in
[9]) resulting in shingle
set size of about S-k+1, where
S is the file size. Later, it computes the image (value) of
each shingle by applying set (say H) of min-wise independent hash
functions (|H|=84
[9]) and then for each
function, selecting the shingle corresponding to the minimum image. On
the other hand, we apply a set of independent hash functions
(typically less than 8) to the chunk set of size on average
é[S/c]ù
where c is the expected chunk size (e.g., c=256 bytes for S=8 KB file).
Third, the size of the feature set (number of
shingles) depends on the sampling technique in shingling. For example,
in
Modm, even some large files might have very few features
whereas small files might have zero features. Some shingling
variants (e.g., Mins, Mod2i) aim to
select roughly a
constant number of features. Our CDC based approach only varies the
chunk size c, to determine the number of chunks as a trade-off
between performance and fine-grained matching. We leave the empirical
comparison with shingling as future work.
In general, a compact Bloom filter is easier to attach as a file
tag and is compared simply by matching the bits.
4.4 Direct Chunk Matching for
Similarity
The chunk-based matching in the second phase, can be directly used to
simultaneously detect similar files between the source and
target. When matching the chunk hashes belonging to a file, we create a
list of candidate files that have a common chunk with the file. The
file with the maximum number of matching chunks is marked as the
similar file. Thus the matching complexity of direct chunk matching is
O(Number of Chunks).
This direct matching technique can also be used
in conjunction with other similarity detection techniques for
validation. While the Bloom filter technique is general and can be
applied even when a database of all file chunks is not maintained,
direct matching is a simple extension of the chunk matching phase.
To evaluate the effectiveness of similarity detection using CDC, we
perform the same set of experiments as discussed in
Section 4.2 for Bloom filters. The
results, as expected, were identical to
the Bloom filter approach. Figures 11, 12, and 13
show the corresponding plots for matching the files 'ChangeLog',
'nt/config.nt' and 'foo', respectively. Direct matching is more
exact as there is no probability of false matching. The
Emacs-20.1/ChangeLog file matched with the Emacs-20.7/ChangeLog
file in 112 out of 128 CDCs (88%).
Similarly, the Emacs-20.7/nt/config.nt file had a non-zero match with
only three Emacs-20.1/* files
with 8 (46%), 9 (53%), 5 (29%) matches out of 17
corresponding to the files nt/config.nt, src/config.in and nt/config.h,
resp. The file 'foo' matched 'foo.1' in 99% of the CDCs.
5 Experimental Evaluation
In this section, we evaluate TAPER using several workloads, analyze
the
behavior of the various phases of the protocol and compare the
bandwidth efficiency, computation overhead, and response times with
tar+gzip, rsync, and CDC.
5.1 Methodology
We have implemented a prototype of TAPER in C and Perl. The chunk
matching in Phase II uses code from the CDC implementation of
LBFS [20] and
uses the SleepyCat software's BerkeleyDB database package for
providing hash based indexing. The delta-compression of Phase IV was
implemented using vcdiff [14].
The experimental testbed used two
933 MHz Intel Pentium III workstations with 512 MB of RAM running
Linux kernel 2.4.22 connected by full-duplex 100 Mbit
Ethernet.
| Software Sources (Size KB)
|
| Workload |
No. of Files |
Total Size
|
| linux-src (2.4.26) |
13235 |
161,973
|
| AIX-src (5.3) |
36007 |
874,579
|
| emacs (20.7) |
2086 |
54,667
|
| gcc (3.4.1) |
22834 |
172,310
|
| rsync (2.6.2) |
250 |
7,479
|
| Object Binaries (Size MB)
|
| linux-bin (Fedora) |
38387 |
1,339 |
| AIX-bin (5.3) |
61527 |
3,704 |
| Web Data (Size MB)
|
| CNN |
13534 |
247 |
| Yahoo |
12167 |
208 |
| IBM |
9223 |
248 |
| Google Groups |
16284 |
251 |
Table 1: Characteristics of the different Datasets
For our analysis, we used three different kinds of
workloads: i) software distribution sources, ii)
operating system object binaries,
and iii) web content. Table 1 details
the different
workload characteristics giving the total uncompressed size and the
number of files for the newer version of the data at the source.
| Workload |
linux-src |
AIX-src |
emacs |
gcc |
| Versions |
2.4.26 - 2.4.22 |
5.3 - 5.2 |
20.7 - 20.1 |
3.4.1 - 3.3.1
|
| Size KB |
161,973 |
874,579 |
54,667 |
172,310
|
| Phase I |
62,804 |
809,514 |
47,954 |
153,649 |
| Phase II |
24,321 |
302,529 |
30,718 |
98,428
|
| Phase III |
20,689 |
212,351 |
27,895 |
82,952
|
| Phase IV |
18,127 |
189,528 |
26,126 |
73,263 |
| Diff Output |
10,260 |
158,463 |
14,362 |
60,215 |
Table 2: Evaluation of TAPER Phases. The numbers
denote
the unmatched data in KB remaining at the end of a phase.
Software distributions sources
For the software distribution workload, we consider the source trees of
the
gcc compiler, the emacs editor, rsync, the Linux kernel, and
the AIX kernel.
The data in the source trees
consists of only ASCII text files. The gcc workload
represents
the source tree for GNU gcc versions 3.3.1 at the targets and
version 3.4.1 at the source. The emacs dataset consists of
the source code for GNU Emacs versions 20.1 and 20.7.
Similarly, the rsync dataset denotes the source code for the
rsync software versions 2.5.1 and 2.6.2, with the addition that 2.6.2
also includes the object code binaries of the source.
The two kernel workloads, linux-src and AIX-src,
comprise
the source tree of the Linux kernel versions 2.4.22 and 2.4.26 and
the source tree for the AIX operating system versions 5.2 and 5.3,
respectively.
Object binaries
Another type of data widely upgraded and replicated is
code binaries. Binary files have different characteristics compared to
ASCII files. To capture a tree of code binaries, we used the
operating system binaries of Linux and AIX. We scanned the entire
contents of the directory trees /usr/bin, /usr/X11R6 and
/usr/lib in RedHat 7.3 and RedHat Fedora Core I distributions,
denoted by linux-bin dataset. The majority of data in these
trees comprises of system binaries and software libraries containing
many object files. The AIX-bin dataset consists of object
binaries and libraries in /usr, /etc, /var, and /sbin
directories of AIX versions 5.2 and 5.3.
Web content
Web data is a rich collection of text, images,
video, binaries, and various other document formats. To get a
representative sample of web content that can be replicated at mirror
sites and CDNs, we used a web crawler to crawl a number of large web
servers. For this, we used the wget 1.8.2 crawler to retrieve
the web pages and all the files linked from them, recursively for an
unlimited depth. However, we limited the size of the downloaded content
to be 250 MB and restricted the crawler to
remain within the website's domain.
The four datasets, CNN, Yahoo, IBM and Google Groups, denote the
content of
www.cnn.com, www.yahoo.com, www.ibm.com, and groups.google.com websites
that was downloaded every day from 15 Sep. to 10 Oct., 2004. CNN is a
news and current affairs site wherein the top-level web pages
change significantly over a period of about a day. Yahoo, a popular
portal on the Internet, represents multiple pages which have small
changes corresponding to daily updates. IBM is the company's
corporate homepage providing information about its products and
services. Here, again the top-level pages change with announcements
of product launches and technology events, while the others relating
to technical specifications are unchanged. For the Google Groups data
set, most pages have numerous changes due to new user postings and
updates corresponding to feedback and replies.
| Workload |
linux-src |
AIX-src |
emacs |
gcc
|
| Phase I |
291 |
792 |
46 |
502 |
| Phase II |
317 |
3,968 |
241 |
762 |
| Phase III |
297 |
3,681 |
381 |
1,204 |
Table 3: Uncompressed Metadata overhead in KB of the
first three TAPER phases.
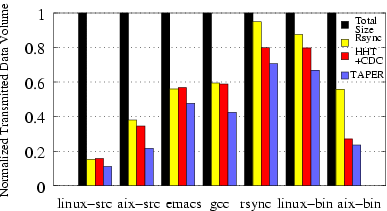
Figure 14: Normalized transmitted data volume
(uncompressed) by Rsync, HHT+CDC, TAPER on Software distribution and
Object binaries. The results are normalized against the total size of
the dataset.
5.2 Evaluating TAPER Phases
As we described earlier, TAPER is a multi-phase protocol where each
phase operates at a different granularity. In this section, we
evaluate the behavior of each phase on different workloads. For each
dataset, we upgrade the older version to the newer version, e.g., Linux
version 2.4.22 to 2.4.26. For each phase, we measure the total size
of unmatched data that remains for the next phase and the total
metadata that was exchanged between the source and the target. The
parameters used for expected and max chunk size in Phase II was 4 KB
and 64 KB, respectively. For Phase III, the block size parameter was
700
bytes. The data for Phase IV represents the final unmatched data that
includes the delta-bytes. In practice, this data would then be
compressed using
gzip and sent to the target. We do not present the final
compressed
numbers here as we want to focus on the contribution of TAPER and not
gzip.
For comparison, we show the size of the output of "diff -r".
Table 2 shows the total unmatched data
that remains
after the completion of a phase for the workloads linux-src,
AIX-src, emacs and gcc. Additionally,
Table 3 shows the metadata that was
transmitted
for each phase for the same workloads. The table shows that the
data reduction in terms of uncompressed bytes transmitted range from
88.8% for the linux-src and 78.3% for the AIX-src to 52.2% for emacs
and 58% for gcc. On the other hand, the overhead (compared to the
original data) of metadata transmission ranged from 0.5% for
linux-src and 0.9% for AIX-src to 1.2% for emacs and 1.4% for gcc.
Observe that the metadata in Phase II and III is in the same ball park
although the matching granularity is reduced by an order of magnitude.
This is due to the unmatched data reduction per phase. The metadata
overhead of Phase I is relatively high. This is partly due to the
strong 20-byte hash SHA-1 hash that is used. Note that the unmatched
data at the end of Phase IV is in the same ball park as the diff
output between the new and old data
version but that computing the latter requires a node to have a copy of
both versions and so is not a viable solution to our problem.
|
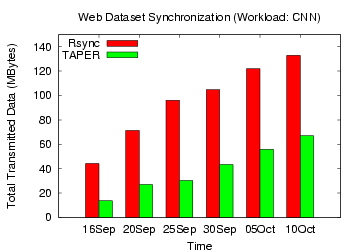
Figure 15: Rsync, TAPER Comparison
on CNN web dataset
|
|
|
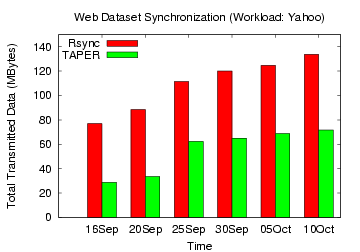
Figure 16: Rsync, TAPER Comparison on
Yahoo web dataset
|
5.3 Comparing Bandwidth
Efficiency
In this section, we compare the bandwidth efficiency of TAPER (in
terms
of total data and metadata transferred) with tar+gzip, rsync, and
HHT+CDC.To differentiate bandwidth savings due to TAPER from data
compression (gzip),
we first illustrate TAPER's contribution to bandwidth savings without
gzip
for software sources and object binaries workloads.
Figure 14 shows the
normalized transmitted data volume by TAPER, rsync, and HHT+CDC for the
given datasets.
The transmitted data volume is normalized against the total size of the
dataset.
For the gcc, AIX-src, and linux-bin
datasets, rsync transmitted about 102 MB, 332 MB, and 1.17 GB,
respectively.
In comparison, TAPER sent about 73 MB, 189 MB, and 896 MB corresponding
to bandwidth savings of 29%, 43% and 24%, respectively for these three
datasets. Overall, we observe that TAPER's improvement over rsync
ranged from 15% to 43%
for software sources and 24% to 58% for object binaries workload.
Using gzip compression, we compare TAPER and rsync with the baseline
technique of tar+gzip.
For the linux-src and AIX-bin data-sets, the
compressed tarball (tar+gzip) of the directory trees, Linux 2.4.26 and
AIX 5.3,
are about 38 MB and 1.26 GB, respectively. TAPER (with compression
in the last phase) sent about 5 MB and 542 MB of difference data, i.e.,
a performance gain of
86% and 57% respectively over the compressed tar output.
Compared to rsync, TAPER's improvement ranged from 18% to 25%
for software sources and 32% to 39% for object binaries datasets.
For web datasets, we marked the data crawled on Sep. 15, 2004 as
the base set and the six additional versions corresponding to the data
gathered after 1, 5, 10, 15, 20 and 25 days. We
examined the bandwidth cost of updating the base set to each of the
updated versions without compression. Figures 15,
16,
17, 18 show the total
data transmitted (without compression) by
TAPER and rsync to update the base version for the web datasets. For
the CNN workload, the data transmitted by TAPER across the different
days ranged from 14 MB to 67 MB, while that by rsync ranged from 44 MB
to 133 MB. For this dataset, TAPER improved over rsync from 54% to 71%
without
compression and 21% to 43% with compression. Similarly,
for the Yahoo, IBM and Google groups workload, TAPER's improvement over
rsync without
compression ranged 44-62%, 26-56%, and 10-32%, respectively.
With compression, the corresponding bandwidth savings by TAPER for
these three workloads ranged
31-57%, 23-38%, and 12-19%, respectively.
|
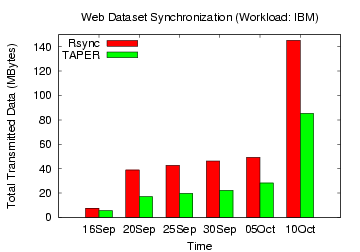
Figure 17: Rsync, TAPER Comparison
on IBM web dataset
|
|
|
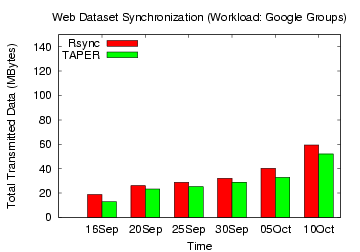
Figure 18: Rsync, TAPER Comparison on
Google Groups web dataset
|
5.4 Comparing Computational
Overhead
In this section, we evaluate the overall computation overhead at the
source machine. Micro-benchmark experiments to analyze the performance
of the individual phases are given in Section 5.5.
Intuitively, a higher computational load at the source would
limit its scalability.
For the emacs dataset, the compressed tarball takes 10.4s of user and
0.64s of system CPU time. The corresponding CPU times for rsync are
14.32s and 1.51s. Recall that the first two phases of TAPER
need only to be computed once and stored. The total CPU times
for the first two phases are 13.66s (user) and 0.88s (system). The
corresponding total times for all four phases are 23.64s and 4.31s.
Thus, the target specific computation
only requires roughly 13.5s which is roughly same as rsync.
Due to space constraints, we omit these results for the other data
sets, but the comparisons between rsync and TAPER are qualitatively
similar for all experiments.
| Chunk Sizes |
256 Bytes |
512 Bytes |
2 KB |
8 KB |
| File Size |
(ms) |
(ms) |
(ms) |
(ms) |
| 100 KB |
4 |
3 |
3 |
2 |
| 1 MB |
29 |
27 |
26 |
24 |
| 10 MB |
405 |
321 |
267 |
259 |
Table 4: CDC hash computation time for different files
and expected chunk sizes
5.5 Analyzing Response Times
In this section, we analyze the response times for the
various phases of TAPER. Since the phases of TAPER include
sliding-block and CDC, the same analysis holds for rsync and any
CDC-based system. The total response time includes the time for i)
hash-computation, ii) matching, iii) metadata exchange, and iv) final
data transmission. In the previous discussion on bandwidth
efficiency, the total metadata exchange and data transmission byte
values are a good indicator of the time spent in these two
components. The other two components of hash-computation and matching
are what we compare next.
The hash-computation time for a single block, used in the sliding-block
phase, to compute a 2-byte checksum and a 4-byte MD4 hash for block
sizes of 512 bytes, 2 KB, and 8 KB, are 5.37ms,
19.77ms, and 77.71ms,
respectively.
Each value is an average of 1000 runs of the experiment.
For CDC, the hash-computation time includes detecting the chunk
boundary, computing the 20-byte SHA-1 signature and populating the
database for indexing. Table 4 shows
the CDC computation times for
different file sizes of 100 KB, 1 MB, and 10 MB, using different
expected chunk sizes of 256 bytes, 512 bytes, 2 KB, and 8 KB,
respectively. The Bloom filter generation time for a 100 KB file (309
CDCs) takes 118ms, 120ms, and 126ms
for 2, 4, and 8 hash functions, respectively.
Figure 19 shows the match time for
sliding-block and CDC
for the 3 file sizes (10 KB, 1 MB and 10 MB) and 3 block sizes (512
bytes, 2 KB, 8 KB). Although the fixed-block hash generation is 2 to 4
times faster
than CDC chunk hash-computation, the
time for CDC matching is 10 to a 100 times faster. The hash-computation
time can be amortized over multiple targets as
the results are stored in a database and re-used. Since the matching
time is much faster for CDC we use it in Phase II where it is used to
match
all the chunks over all the files.
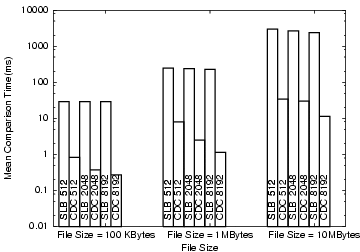
Figure 19: Matching times for CDC and
sliding-block (SLB).
6 Related Work
Our work is closely related to two previous hash-based techniques:
sliding block used in rsync [2],
and CDC introduced in LBFS [20].
As discussed in Section 2, the
sliding-block technique works well only under certain conditions:
small file content updates but no directory structure changes (renames,
moves, etc.).
Rsync uses sliding block only and thus performs poorly in
name-resilience, scalability, and matching time. TAPER, however, uses
sliding block in the third phase when these conditions hold.
The CDC approach, in turn, is sensitive to the chunk size parameter:
small
size leads to fine-grained matching but high metadata whereas large
chunk size
results in lower metadata but fewer matches.
Some recent studies have proposed multiresolution partitioning of data
blocks to address the problem of the optimal block-size both in the
context of rsync [16]
and CDC [12].
This results in a trade-off between bandwidth savings and the number of
network round-trips.
Previous efforts have also explored hash-based schemes based on sliding
block and CDC for duplicate data suppression in different contexts.
Mogul et al. use MD5 checksums over web payloads to eliminate redundant
data transfers over HTTP links [19].
Rhea et al.
describe a CDC based technique that removes duplicate payload transfers
at finer granularities [23]
compared to Mogul's approach.
Venti [21] uses
cryptographic hashes on CDCs to reduce duplication
in an archival storage system. Farsite [3], a secure, scalable distributed file system,
employs file level hashing to reclaim storage space from duplicate
files. You et al. examine whole-file hashing and CDCs to suppress
duplicate data
in the Deepstore archival storage system [27].
Sapuntzakis et al. compute SHA-1 hashes of files
to reduce data transferred during the migration of appliance states
between machines [24].
For similarity detection, Manber [17] originally proposed the shingling
technique to find similar files in a large file system.
Broder refined Manber's technique by first using a deterministic sample
of the hash values (e.g., min-hashing)
and then coalescing multiple sampled fingerprints into super-fingerprints [5,7,6].
In contrast, TAPER uses Bloom filters [4] which compactly encode the CDCs of a given
file to
save bandwidth and performs fast bit-wise AND of Bloom filters for
similarity detection. Bloom filters have been proposed to estimate the
cardinality of set
intersection [8] but have
never been applied for near-duplicate elimination in file systems.
Further improvements on Bloom filters can be achieved by using
compressed Bloom filters [18],
which reduce the number of bits transmitted over the network at the
cost of increasing storage and
computation costs.
7 Conclusion
In this paper we present TAPER, a scalable data replication
protocol
for replica synchronization that provides four
redundancy elimination phases to balance the trade-off
between bandwidth savings and computation overheads.
Experimental results show that in comparison with rsync, TAPER reduces
bandwidth
savings by 15% to 71%, performs faster matching, and scales
to a larger number of replicas. In future work, instead of
synchronizing data on a per-client basis, TAPER can (a) use multicast
to transfer the common updates to majority of the clients, and later
(b) use cooperative synchronization where clients exchange small
updates
among themselves for the remaining individual differences.
8 Acknowledgments
We thank Rezaul Chowdhury, Greg Plaxton, Sridhar Rajagopalan, Madhukar
Korupolu, and
the anonymous reviewers for their insightful comments.
This work was done while the first author was an intern at IBM Almaden
Research Center.
This work was supported in part by the NSF (CNS-0411026), the Texas
Advanced Technology Program (003658-0503-2003), and an IBM Faculty
Research Award.
References
- [1]
- https://th.informatik.uni-mannheim.de/people/lucks/hashcollisions/.
- [2]
- Rsync https://rsync.samba.org.
- [3]
- A. Adya, W. J. Bolosky, M. Castro, G. Cermak,
R. Chaiken, J. R. Douceur, J. Howell, J. R. Lorch,
M. Theimer, and R. P. Wattenhofer. FARSITE: Federated,
available, and reliable storage for an incompletely trusted
environment. In OSDI, Dec. 2002.
- [4]
- B. H. Bloom. Space/time trade-offs in hash coding with
allowable errors. Commun. ACM, 13(7):422-426, 1970.
- [5]
- A. Z. Broder. On the resemblance and containment of
documents. In SEQUENCES, 1997.
- [6]
- A. Z. Broder. Identifying and filtering near-duplicate
documents. In COM, pages 1-10, 2000.
- [7]
- A. Z. Broder, S. C. Glassman, M. S. Manasse, and
G. Zweig. Syntactic clustering of the web. In WWW, 1997.
- [8]
- A. Z. Broder and M. Mitzenmacher. Network applications
of Bloom filters: A survey. In Allerton, 2002.
- [9]
- D. Fetterly, M. Manasse, and M. Najork. On the
evolution of clusters of near-duplicate web pages. In LA-WEB,
2003.
- [10]
- V. Henson. An analysis of compare-by-hash. In HotOS IX,
2003.
- [11]
- D. Hitz, J. Lau, and M. Malcolm. File system
design for an NFS file server appliance. Technical Report TR-3002,
Network Appliance Inc.
- [12]
- U. Irmak and T. Suel. Hierarchical substring caching
for efficient content distribution to low-bandwidth clients. In WWW,
2005.
- [13]
- N. Jain, M. Dahlin, and R. Tewari. TAPER: Tiered
approach for eliminating redundancy in replica synchronization.
Technical Report TR-05-42, Dept. of Comp. Sc., Univ. of Texas at
Austin.
- [14]
- D. G. Korn and K.-P. Vo. Engineering a differencing and
compression data format. In USENIX Annual Technical Conference,
General Track, pages 219-228, 2002.
- [15]
- P. Kulkarni, F. Douglis, J. D. LaVoie, and
J. M. Tracey. Redundancy elimination within large collections of
files. In USENIX Annual Technical Conference, General Track,
pages 59-72, 2004.
- [16]
- J. Langford. Multiround rsync. Unpublished manuscript.
https://www-2.cs.cmu.edu/~jcl/research/mrsync/mrsync.ps.
- [17]
- U. Manber. Finding similar files in a large file system. In USENIX
Winter Technical Conference, 1994.
- [18]
- M. Mitzenmacher. Compressed Bloom filters. IEEE/ACM
Trans. Netw., 10(5):604-612, 2002.
- [19]
- J. C. Mogul, Y.-M. Chan, and T. Kelly. Design,
implementation, and evaluation of duplicate transfer detection in HTTP.
In NSDI, 2004.
- [20]
- A. Muthitacharoen, B. Chen, and D. Mazieres. A
low-bandwidth network file system. In SOSP, 2001.
- [21]
- S. Quinlan and S. Dorward. Venti: a new approach to
archival storage. In FAST, 2002.
- [22]
- M. O. Rabin. Fingerprinting by random polynomials. Technical
Report TR-15-81, Harvard University, 1981.
- [23]
- S. C. Rhea, K. Liang, and E. Brewer. Value-based
web caching. In WWW, pages 619-628, 2003.
- [24]
- C. P. Sapuntzakis, R. Chandra, B. Pfaff,
J. Chow, M. S. Lam, and M. Rosenblum. Optimizing the
migration of virtual computers. In OSDI, Dec. 2002.
- [25]
- R. Thurlow. A server-to-server replication/migration
protocol. IETF Draft May 2003.
- [26]
- X. Wang, Y. Yin, and H. Yu. Finding collisions in
the full SHA1. In Crypto, 2005.
- [27]
- L. You, K. Pollack, and D. D. E. Long. Deep
store: an archival storage system architecture. In ICDE,
pages 804-815, 2005.
|






 , Mike Dahlin
, Mike Dahlin