Pp. 103–116 of the Proceedings

Myriad: Cost-effective Disaster Tolerance

Fay Chang, Minwen Ji, Shun-Tak A. Leung, John MacCormick, Sharon E. Perl, Li Zhang
Compaq Systems Research Center
Palo Alto, CA, 94301

Abstract

The key technical contribution of the paper is a protocol permitting cross-site checksums to be updated in such a way that data recovery is always possible. Another important contribution is the specification of a protocol for recovering from disasters, explicitly verifying the claim of disaster tolerance. Further, it is shown by direct calculation and analytical modeling that Myriad compares favorably with mirroring in terms of both total cost of ownership and reliability.

1  Introduction

A geoplex is a collection of geographically distributed sites, each consisting of servers, applications, and data [7]. The sites of a geoplex cooperate to improve reliability and/or availability of applications and data through the use of redundancy. Data redundancy in geoplexes typically takes the form of mirroring , where one or more full copies of the logical data are maintained at remote sites. In this paper we present alternative approaches to mirroring for cross-site data redundancy in geoplexes. While the alternatives are not as generally applicable as mirroring, they have noticeably lower cost, provide additional flexibility, and are appropriate for a significant class of applications.

Mirroring has a number of desirable properties. It is conceptually simple, and does not compromise performance when it operates in an asynchronous mode for remote updates. Its recovery procedure is simple. In addition to the ability to reconstruct data after a site failure, it offers the choice of active-active configurations (where all sites are actively processing some work) and active-passive configurations (where fast failover is possible from the primary site to a secondary site). On the negative side, mirroring has a high cost because the amount of storage required for the logical data must be doubled or more depending on the number of mirror copies. For very high reliability, more than one mirror copy generally is required. While the high cost for remote mirroring has been accepted by customers with mission-critical applications, such as online transaction processing systems, a geoplex is hardly a low-cost product available for many other applications with large data sets, such as data mining and scientific computing.

We investigate the possibility of offering more flexible, often lower, pricing of a geoplex by supporting a variety of data redundancy schemes across sites. The system, called Myriad, uses redundancy schemes based on erasure codes [16] (error-correcting codes where the position of the error is known). Erasure codes form the basis for the approaches to disk array redundancy known as RAID levels 3, 4, 5, and 6 [10]. We study this approach for maintaining redundancy of data spread across geographically distant sites rather than across disks in a disk array.

We start by examining the reasons erasure codes have not previously been employed in geoplexes. It is perceived that although erasure codes reduces the number of disks needed for a given amount of data, the dollar saving is insignificant because disks account for only a small portion (10-25%) of the total cost of ownership (TCO) of the entire storage solution. There is a perception that the software implementation of erasure codes across servers offers lower reliability than mirroring, and it is too complicated to be commercializable even within a local site.

The TCO includes all costs attributable to a storage system over its lifetime, including purchase, installation, power, floor space and human labor costs for administering and maintaining the system. By analyzing components of the TCO, we discover that requiring less hardware lowers not just the purchase cost but also other TCO components such as environmental and administration costs. Therefore, a scheme using less hardware could reduce the TCO by a noticeable amount. For example, our analysis shows that, in order to implement a geoplex across 5 sites with 20 terabytes of data on each site, single mirroring costs about 80% more than the original (non-redundant) scheme, while a parity-based scheme (an instance of an erasure code) costs only about 40% more. Section 3 presents our TCO analysis.

We also compare the reliability of various cross-site redundancy schemes, primarily through analytical modeling. We derive equations for the mean time to data loss (MTTDL) of these schemes. Across a spectrum of system configurations, we find, not surprisingly, that the MTTDL of a Myriad scheme with one checksum (single redundancy) is worse than that of a mirrored system but much better than if there is no cross-site redundancy. Moreover, the MTTDL of a Myriad scheme with two checksums (double redundancy) is worse than that of a double mirroring system but much better than that for a mirrored system. Section 4 discusses the results of the reliability analysis in more details.

The complexity of non-mirroring redundancy schemes is an issue for both local-area and cross-site storage systems. However, we have observed enough differences in the two systems to believe that their protocols should be quite different. In a local-area parity scheme, such as the storage layer in xFS [20], the local-area network (LAN) connecting servers is assumed to be fast and cheap (e.g., Ethernet). The design goal is to parallelize reads and writes across disks for large aggregate bandwidth and to present an image of a single system. Therefore, the design challenges lie in data layout, coordination across servers, cache coherence, and decentralization of control.

In the systems we are targeting, the wide-area network (WAN) connecting sites is assumed to be slow and expensive (e.g., leased T1 or T3 lines). Consequently, applications running on each site are configured to be independent of applications running on other sites; in other words, a logical piece of data is not stored across sites. For example, suppose a hospital chain has branches in multiple cities and each branch has its own file system for local employees and patients. In order to implement Myriad-style data redundancy across branches, one only needs to add a certain amount of physical storage to each branch, which will be dedicated to storing the redundancy information (i.e., checksums) of data on other sites. Although branches may manage to gain access to each other by mounting remote file systems, the storage layout of the local file systems does not have to be changed. Therefore, at the block storage level, there is no issue about parallelism or single-system image across sites. Rather, the goal of our design is to reliably and consistently deliver data to the remote checksum sites for protection while hiding the long latency of WAN from the critical path of data access.

We have designed a cross-site update/recovery protocol that supports redundancy based on erasure codes, where the number of data and checksum disks may vary. As it happens, mirroring is a degenerate case of erasure coding where there is a single data block per group of checksum blocks, so our protocol supports mirroring as well. However, it is expected to have higher complexity and overhead than a protocol designed solely for mirroring. There are two major reasons for this: (1) the reconstruction of data with a non-mirroring scheme is substantially more difficult than with a mirroring scheme; (2) the operation of updating a checksum is not idempotent, in contrast to that of a mirror. Nevertheless, we design our protocol so that it requires no more WAN bandwidth than a pure mirroring protocol. Sections 5 and 6 discuss our design in detail.

2  System Overview

A Myriad system achieves disaster tolerance by storing data at a number of geographically distinct sites. Each site consists of disks, servers, a LAN, and some local redundancy such as hardware RAID-5; the sites are connected by a WAN. Each site is assumed to employ a storage area network (SAN).

The essential idea behind Myriad is that, in addition to any local redundancy such as RAID, each block of data participates in precisely one cross-site redundancy group. A cross-site redundancy group is a set of blocks, one per site, of which one or more are checksum blocks. Thus, the blocks in a given group protect one another's data. The simplest possible example is single parity, in which one of the blocks is the XOR of the others - this is equivalent to running a distributed form of RAID-5. The system can reconstruct the current, correct contents of a lost site on a replacement site.

Much greater disaster tolerance can be achieved by using more redundancy. For instance, one can use all but two of the blocks in every cross-site redundancy group for data, and use the remaining two blocks as checksums computed using a Reed-Solomon erasure code [2]. This type of the system, which is equivalent to running distributed RAID-6, can recover from up to two site losses.

An application using a Myriad storage system must satisfy two properties:

1. Dispersed data: data is dispersed over multiple sites. The Myriad protocol (section 6) formally requires as few as two sites (single redundancy) or three sites (double redundancy), but as discussed in section 3, the efficiency gains of the Myriad system (as compared with mirroring) are more compelling when there are more (say 5 or more). In addition, the amount of data at each site should be roughly equal; otherwise, the efficiency gains are again reduced. (This is the same as the problem of using disks of different sizes in a RAID-5 array.)
2. Local computation: computations on the data are collocated with the data. In other words, an application running at a given site does not access data at other sites. This assumption is motivated by the economic justification of the Myriad approach: if computations are not local, the cost of WAN bandwidth is likely to exceed Myriad's cost benefits which result from using less physical storage.

A relatively broad class of storage customers meet both the ``dispersed data'' and the ``local computation'' conditions. A typical such customer has several different sites, each of which runs its own application and storage system. For example, different sites might perform various payroll, finance, and technical functions. Alternatively, as with the example of a hospital chain given earlier, the sites could be running independent instantiations of the same application, but using only local data. Another potential customer for Myriad is an application service provider (ASP) or storage service provider (SSP) that wants to offer disaster tolerance to their customers cost-effectively.

3  Total Cost of Ownership

The present paradigm for achieving disaster tolerance in a storage system is to mirror all data at a remote site. However, mirroring is expensive: the amount of physical data is twice the amount of logical data (often referred to as ``100% space overhead''), so one must purchase and administer twice as much storage as for a basic (disaster-vulnerable) system. As described later, a typical Myriad system with 5 sites might have only 20-40% space overhead, while retaining or even improving on the disaster tolerance of a mirrored system. So the physical requirement and hence purchase cost for Myriad are as much as 40% ( = 1-[(100+20)/(100+100)]) less than those for mirroring. Although the purchase cost of a storage system is widely known to be only a small fraction of the TCO (reports estimate 10-25% [1,12,18]), this section will show by explicit calculation that a Myriad system would still represent significant TCO savings over a mirrored system.

3.1  Cost Model and Assumptions

A good starting point for calculating the TCO of the system is a report by Gartner Group [1], which estimates the components for the storage TCO of a single-site system; the estimates are shown in Figure 1. In the following analysis, the Hardware Management category is combined with Administration, and the Downtime category is eliminated since it is an opportunity cost related to system reliability.

Figure 1: Storage TCO (Source: Gartner, ``Don't Waste Your Storage Dollars: What you Need To Know'', Nick Allen, March 2001 [1].)

We first determine what proportion of each cost category scales with the physical, as opposed to logical, amount of storage. Specifically, let Physical be the amount of physical storage, Logical the amount of logical storage (i.e., storage for user data, including local redundancy), and C_admin, C_purch, C_env and C_backup the administration, purchase, environmental and backup/restore costs respectively. Each type of cost is modeled as a linear combination of Physical and Logical. For example, C_admin = _admin (_admin Physical+ (1-_admin) Logical) Intuitively, each category is parameterized by l Î [0,1] specifying how much the cost depends on Physical rather than Logical. This defines an ``effective storage size'' lPhysical+(1-l)Logical for the category. The absolute cost of the category is obtained by multiplying by a coefficient a, which is the category cost in $/GB of effective storage.

Appropriate values for the l and a parameters can be inferred as follows. First, l_purch=1 by definition. Environmental costs include power, UPS, and floor space, all of which scale directly with Physical, so l_env=1 also. The value of a_purch can be determined directly from published component prices (see Figure 2 for an example), and so we express the remaining a-values in terms of a_purch. Following the proportions in Figure 1, we take a_admin=[ 16/20] a_purch, a_env=[ 14/20] a_purch, a_backup=[ 30/20] a_purch. That leaves l_backup and l_admin. We estimate l_backup to be 0. This is conservative in that that it makes a mirrored solution look as good as possible in comparison to Myriad. As for l_admin, by itemizing the tasks of a system administrator and considering whether each depends primarily on physical or logical data size, we estimate l_admin to be 0.5. (Tasks scaling primarily with logical data size include most software management tasks, such as array control management, cross-site redundancy management, snapshot operation, and local network management. Tasks scaling primarily with physical data size include monitoring, reporting on, and altering physical storage resources, and implementing volume growth.) But since the value of l_admin may be controversial, we leave it as a free variable for now.

Figure 2: Purchase cost breakdown for a typical 20TB storage system, based on component prices posted on Compaq and Asante web sites.

Let Overhead be the space overhead of the remote redundancy scheme, so that Physical = (1+Overhead) × Logical, and let C_WAN denote the cost of WAN bandwidth consumed by the system over its lifetime. After substitutions and simplifications, we arrive at TCO = _purch  Logical + C_WAN.

For concreteness, consider a storage system with 100TB of logical data distributed over five sites (or 20TB/site). If each site runs RAID-5 locally in hardware, and reserves one hot spare in every 14-drive enclosure, the purchase cost of physical equipment is about $823K/site for the particular choice of components listed in Figure 2; this corresponds to a value of a_purch=$42/GB.

To calculate the lifetime WAN cost C_WAN, note that WAN bandwidth is only for redundancy information updates because client data accesses are local. Assume that bandwidth costs $500/Mbps/month/site, that the lifetime of the system is five years, that all the data is overwritten on average twice per year, and that the system achieves an average 33% utilization of the purchased bandwidth, due to burstiness. (The bandwidth cost is typical of ISPs at the time of writing; the other numbers are just examples chosen here for concreteness - the actual data write rate and burstiness are highly application-dependent.) This gives C_WAN = Logical bandwidth cost lifetime
= $4.8/ The resulting bandwidth requirement between any two sites is 16Mb/s. The bandwidth costs are doubled for double redundancy, whether in a mirroring scheme or in Myriad. Additional bandwidth is required for recovery; this adds less than 1% to the WAN cost using worst-case parameters from the next section, assuming that the price for extra bandwidth is the same as for standard bandwidth. Although ISPs do not currently sell bandwidth in this ``expandable'' manner, this may change in the near future [8].

3.2  Results and Discussion

Figure 3(a) shows the TCO for such a system with varying values for the space overhead of the remote redundancy scheme, assuming five sites and l_admin=0.5. Note that Myriad with one checksum site (remote RAID-5, Overhead =25%) costs 22% less than a standard singly-mirrored system (Overhead =100%), and Myriad with two checksum sites (remote RAID-6, Overhead =67%) costs 27% less than double-mirroring (Overhead =200%). Figure 3(b) shows a breakdown into cost categories.

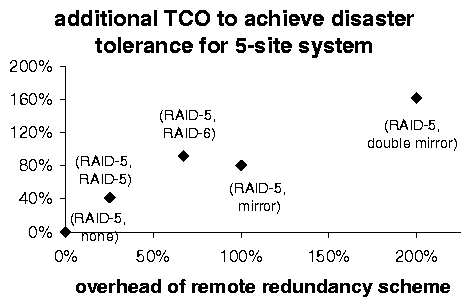
(a)

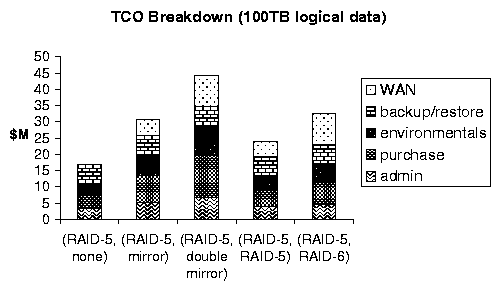
(b)

Our sensitivity analysis finds that these results are not too sensitive to l_admin. They are somewhat sensitive, however, to the assumptions about WAN bandwidth requirements. If the between-site requirement is in fact half the earlier estimate (i.e., 8Mb/s), Myriad's cost advantages are 24% and 30%. If the requirement is twice that (i.e., 32Mb/s), they drop to 19% and 22%. Also note that the cost of a Myriad system with two checksum sites is only 6% above the cost of a standard singly-mirrored system. As Section 4 shows, this small additional cost buys significantly more reliability.

Of course, the model (1) is not sufficiently realistic to predict the costs of all storage systems - such systems vary too widely for any single formula to be accurate. Nevertheless, we believe this model conveys the essence of how TCO depends on physical data size, and hence yields a valid comparison between the mirroring and Myriad approaches.

Finally, the above analysis assumes that the raw data cannot be significantly compressed (perhaps because it is already compressed). Otherwise, mirrored systems could become more attractive by compressing their remote copy.

4  Reliability

The previous section argued that, contrary to common supposition, the cost of disaster tolerance is highly dependent on the storage overhead of the cross-site data redundancy scheme. In this section, we study the reliability of different cross-site data redundancy schemes and demonstrate that lower-overhead schemes can provide substantial reliability benefits.

We use the mean time to data loss (MTTDL) as our reliability metric. In analyzing the MTTDL of a multi-site storage system, we assume that each site is already using some local data redundancy scheme. In particular, we assume that the blocks at each site are stored on hardware RAID boxes that are implementing a RAID level that provides some redundancy (i.e., any level other than RAID-0). This is a reasonable assumption because hardware RAID boxes enable fast redundant updates, and both good performance during and fast recovery from the common failure cases. We also make the simplifying assumption that only two types of components need to be considered in our reliability analysis - hardware RAID boxes and sites - and that failures of different components are exponentially distributed [10], independent, and complete (i.e. when a component fails, all blocks on that component are lost). Note that the analysis is a comparison of hardware failures only; other types of failure (such as software and operator errors) can be significant sources of data loss, but they are not addressed here.

Consider a storage system with D data (as opposed to checksum) blocks spread out over N sites. Assume that each hardware RAID box contains approximately B raw blocks not used for the local parity scheme, such that there are R = D/B RAIDs-worth of data in the system. Let t_r and t_s represent the mean time to failure of a hardware RAID box and a site, respectively, and r_r and r_s represent the mean time to repair of a hardware RAID box and site, respectively. Finally, let binomial(n,r) be the standard binomial coefficient.

We calculate the MTTDL of the system with five different cross-site redundancy schemes: no cross-site redundancy, cross-site RAID-5, cross-site mirroring, cross-site RAID-6, or cross-site double mirroring. It's important to realize that MTTDL for cross-site RAID depends on the precise layout of redundancy groups. Take cross-site RAID-5 as an example: if the ``parity partners'' of blocks in a given physical RAID box are distributed randomly across boxes at other sites, any pair of box failures at distinct sites causes data loss. We call this the ``worst-case layout'', and include its results primarily for completeness. An implementation would certainly avoid this worst case, and strive to achieve the ``best-case layout'', in which blocks from any physical RAID box partner with blocks from only one box at each other site: with this layout, fewer pairs of failures lead to data loss, and the MTTDL is larger. It's easy to achieve this best case for mirroring, so only the best-case results are shown for the mirroring schemes.

Under these assumptions, standard manipulations of the exponential distribution [10,19] lead to the formulas for 1/MTTDL shown in Figure 4. To obtain good performance, it is assumed that write calls to the storage system are permitted to return as soon as the write has been committed in a locally redundant fashion. Therefore, MTTDL should also include terms for failures of RAID boxes which have data that has been committed locally but not remotely. However, the amount of ``remotely uncommitted'' data can be traded off with local write performance in a manner analogous to the trade-off between locally unprotected data and write performance in an AFRAID system [17]. If one assumes the network is reliable, such data loss can be made vanishingly small, and accordingly we neglect it here. The investigation of unreliable networks and details of the write performance-data loss trade-off are left to future work.

cross-site scheme	1/MTTDL
None	[ R/(tr)] + [ N/(ts)]
RAID-5 Worst	[(NR2 rr)/((N-1)tr2)] + [(NR(rr+ rs))/(trts)] + [(N(N-1) rs)/(ts2)]
RAID-5 Best	[(NRrr)/(tr2)] + [(NR(rr+ rs))/(trts)] + [(N(N-1) rs)/(ts2)]
Mirror	[(2 Rrr)/(tr2)] + [(2 R(rr+ rs))/(trts)] + [(Nrs)/(ts2)]
RAID-6 Worst	[(3 binomial(N,3) R3 rr2)/((N-2)3tr3)] + [( binomial(N,2) R2 rr(rr+ 2rs))/((N-2) tr2 ts)] + [( binomial(N,2) Rrs(2rr+ rs))/(trts2)] + [(3 binomial(N,3) rs2)/(ts3)]
RAID-6 Best	[( binomial(N,2) Rrr2)/(tr3)] + [( binomial(N,2) Rrr(rr+ 2rs))/(tr2 ts)] + [( binomial(N,2) Rrs(2rr+ rs))/(trts2)] + [(3 binomial(N,3) rs2)/(ts3)]
Double Mirror	[(3 Rrr2)/(tr3)] + [(3 Rrr(rr+ 2rs))/(tr2 ts)] + [(3 Rrs(2rr+ rs))/(trts2)] + [(Nrs2)/(ts3)]

Figure 4: Formulas for 1/MTTDL for various redundancy schemes

Figure 5 shows MTTDL of five-site storage systems, calculated using the equations above. Each graph shows MTTDL for storage systems that contain some particular amount of data, such that results are shown for a wide range of potential storage system sizes (approximately 10 TB to 1 PB, assuming the components listed in Figure 2). Reliability is calculated using a set of conservative failure parameters, and a set of more optimistic failure parameters. For example, our conservative t_r (RAID box MTTDL) is 150 years, which is less than the MTTF of a single disk drive. Note that, in contrast to some previous work [10,17], our t_r includes only failures that cause data loss. For example, we are not including the common case of a RAID controller failure after which all the data can be retrieved simply by moving the disks to another RAID box. NVRAM failures were also neglected.

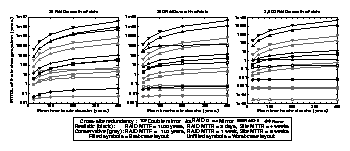
Figure 5: (See a more legible figure in postscript here.) Mean time to data loss for different cross-site redundancy schemes. The results on each graph are for systems with the same amount of logical data D, but different amounts B of data per RAID box, and hence differing values of R = D/B, the total number of RAID boxes. Left: R =25. Middle: R=250. Right: R=2500.

We also developed an event-driven simulator to investigate factors that were difficult to include in the analytical model. In particular, we investigated whether temporary outages (of sites and hardware RAID boxes) or WAN bandwidth limitations substantially changed the results shown above. We found that both outages and WAN bandwidth limitations did shift the curves, but the shifts were small and did not change our conclusions. The intuition behind why the shifts were small is that, in both cases, the effect is essentially the same as slightly increasing the mean times to recovery, r_s and r_r.

The most important observation to be made from Figure 5 is that if blocks are distributed according to a ``best-case layout'', the MTTDL of a RAID-5 system is 2-3 times worse than that of a mirroring system, but much better (around 100 times better) than that of a system with no cross-site redundancy. Furthermore, the MTTDL of a RAID-6 system is worse (by a factor of 10 or so) than that of a double mirroring system, but much better (50-1000 times better) than for a mirrored system. A final summary of the TCO and reliability analyses, using only the base case numbers, is:

where all the numbers are multipliers based on the index ``none'' = 1.

5  Cross-Site Redundancy

We now go on to describe our design for cross-site redundancy based on erasure codes. This section gives an overview of how we maintain redundancy information, including in particular a static scheme for grouping blocks across sites. The next section describes our protocol for update and recovery.

In a bird's eye view of Myriad, local storage systems on different sites, each serving only local clients, cooperate to achieve disaster tolerance for client data. On each site, the local storage system provides a logical disk abstraction to its clients. Clients see only a logical address space divided into blocks of some fixed size, which we call logical blocks. Each logical block is identified by its logical address. Clients read or write logical blocks; the storage system manages physical data placement. Such a storage system in itself poses many important design issues, but they are beyond the scope of this paper. Petal [14] is one such system.

Local storage systems on different sites cooperate to protect data against site disasters by forming cross-site redundancy groups. A cross-site redundancy group (or ``group'' for short) consists of logical blocks (which we call data blocks since they contain client data), and checksum blocks, which contain checksums computed from the data blocks. The data and checksum blocks in a group come from different sites, which we call the data sites and checksum sites of the group. Each group is globally identified by a group id, and each data block by its site and (site-specific) logical address.

To tolerate at most m simultaneous site disasters, each group should consist of n (n > 1) data blocks and m (m > 1) checksum blocks for a geoplex with n+m sites. As for the encoding of the checksum, similar to previous approaches (e.g. [2]), we use a Reed-Solomon code ([16] Ch. 9) to allow incremental update. In other words, a checksum site can compute the new checksum using the old checksum and the XOR between the old and new contents of the data block updated, instead of computing the new checksum from scratch. It degenerates to parity for m=1.

Blocks can be grouped in various ways. In our scheme, we require the checksum blocks be distributed so that they rotate among the sites for logically consecutive data blocks at each individual site. This can be done by using some simple static function to map each data block to a group number and a site number. The following is the function we use. The checksum sites for group g are sites (g-j)\mod N, where 0 £ j < m. The bth data block at site s is mapped into group g, where

g = ì í î b+m·(ë(b-s)/nû+1) s £ n, b+s-n+m·ëb/nû s > n.

It can be verified that this formula realizes a layout satisfying the requirement. Similarly, we can write a formula to compute b from s and g.

6  Update and Recovery

When a client updates a data block, we must update the corresponding checksum blocks. Here, we face two challenges that remote mirroring does not. First, unlike a mirror update, the incremental calculation of a checksum is not idempotent and so must be applied exactly once. Second, a checksum protects unrelated data blocks from different sites; therefore, the update and recovery processes of a data block may interfere with those of other blocks in the same redundancy group; for example, inconsistency between a data block and its checksum affects all data blocks in the group, while inconsistency between a data block and its mirror affects no other blocks.

Therefore, we want our protocol to ensure the idempotent property of each checksum update, and to isolate as much as possible the update and recovery processes of each data block from those of others. And, as in remote mirroring cases, we also attempt to keep remote updates from degrading local write performance.

6.1  Update

6.1.1  Invariants

An important goal of our update protocol is to ensure that redundancy groups are always ``consistent'' and hence can be used for recovery whenever needed. Let n be the number of data blocks in a redundancy group, m be the number of checksum blocks, d_i, 1 £ i £ n be the content of the ith data block, c_j, 1 £ j £ m be the content of the jth checksum block, and C_j, 1 £ j £ m be the jth checksum operation. The group {d₁,...,d_n,c₁,...,c_m} is consistent if and only if "j, 1 £ j £ m,c_j==C_j({d_i | 1 £ i £ n}). The checksums, {c_j | 1 £ j £ m}, are consistent with each other if and only if they belong in the same consistent group.

We maintain consistency by writing the new content of a data block (called a new version) in a new physical location instead of overwriting the old content in place, a technique known as shadow paging or versioning. Each new version is identified by a monotonically increasing version number. Accordingly, a checksum can be uniquely identified by a version vector consisting of version numbers of the (data block) versions from which this checksum is computed.

We say that a checksum block c_j is consistent with a data version d_i,vi and vice verse if and only if there exists a set O of versions of other data blocks in the group, i.e. O={d_k,vk | 1 £ k £ n, k ¹ i}, such that c_j==C_j({d¢| d¢==d_i,vi || d¢ Î O}. We say that a data version d_i,vi^* is stable at a given time if and only if all checksum sites are capable of providing a consistent checksum for that version at that time. In contrast, a data version that has not been stable is called outstanding.

However, the fact that every checksum site is capable of providing a consistent checksum for every data block in a redundancy group does not guarantee the group consistency, because a checksum site may not be capable of providing a checksum that is consistent with all data blocks. Therefore, we introduce the concept of set consistency. Let S be a set of data versions, i.e. S={d_il | 1 £ l £ n¢}, where n¢ is the size of S, 1 £ n¢ £ n, and "l, d_il is from data site i_l. A checksum block c_j is consistent with S or vice verse if and only if there exists a set O of versions of other data blocks in the group, i.e. O={d_k | 1 £ k £ n && "l, k ¹ i_l}, such that c_j==C_j({d¢| d¢ Î S || d¢ Î O}).

We maintain the following two invariants in our update protocol:

1. At any time, at least one stable version of each data block exists.
2. If it is capable of providing a consistent checksum for each individual data version in the set S={d_il | 1 £ l £ n¢}, then a checksum site is capable of providing a consistent checksum for the entire S.

We can infer the following:

1. At any time, there exists a set S^* of stable data versions, i.e. S^*={d_i^* | 1 £ i £ n}, and each checksum site is capable of providing a consistent checksum for each individual data version d_i^* in S^*. (Invariant 1)
2. Each checksum site j is capable of providing a consistent checksum c_j^* for the entire S^*. (Invariant 2)
3. The redundancy group {d₁^*,...d_n^*,c₁^*,...c_m^*} is consistent. (Definition of group consistency)

Therefore, the redundancy group is always consistent and can be used for recovery.

We believe that the versioning approach permits a simpler, less error-prone protocol than an update-in-place approach. Because recovery never relies on blocks in transition states, we need not deal with detecting and correcting such states.

6.1.2  Two-Phase Commit

A naive way of guaranteeing at least one stable version per block (invariant 1) is to keep all old versions and their checksums. To save space, however, we should delete old versions and reclaim their physical storage as soon as a new stable version is created.

We maintain invariant 1 without storing unnecessary old versions by implementing the transition from an old stable version to a new one with a two-phase commit protocol across the data site and all checksum sites. In the prepare phase, each site writes enough information to local persistent storage to ensure that, in the face of system crashes and reboots, it will be capable of providing either the new data version (if it is the data site) or a consistent checksum for the new data version (if it is a checksum site). When all sites have reached the commit point, i.e. have completed the writes, they proceed to the commit phase, i.e. delete the old versions. Site/network outages may delay the communications across sites, but we ensure that the operation will proceed and the unnecessary blocks will be reclaimed once the the communications are reestablished (Section 6.1.3). The update process for a new data version will be aborted only if there is data loss in the redundancy group during the prepare phase, and there are not enough surviving sites to recover the new version. If the process is aborted, the new version will be deleted and the old kept. In fact, the decision for an abort cannot be made until the lost sites have been recovered (Section 6.2).

Messages and operations:

1. MyriadWrite(laddr, new_data)
2. DiskWrite(new_paddr, new_data)
3. AddToLog(laddr, new_vernum, new_paddr)
4. WriteCompleted
5. old_data ¬ DiskRead(old_paddr), delta ¬ old_data Å new_data
6. UpdateRequest(data_site_id, laddr, new_vernum, delta)
7. DiskWrite(delta_addr, delta)
8. AddToLog(group_id, data_site_id, new_vernum, delta_addr)
9. UpdateReply(checksum_site_id, laddr, new_vernum)
10. UpdateMap(laddr, new_paddr, new_vernum), FreeBlock(old_paddr)
11. CommitRequest(data_site_id, laddr, new_vernum)
12. RemoveFromLog(laddr, new_vernum)
13. old_checksum ¬ DiskRead(checksum_addr), new_checksum ¬ ChecksumOp(old_checksum, delta)
14. DiskWrite(checksum_addr, new_checksum)
15. FreeBlock(delta_addr), RemoveFromLog(group_id, data_site_id, new_vernum)

Figure 6 shows the steps in the update protocol.

When a client writes to a (logical) data block, we create a new outstanding data version by writing the data into a free physical block and logging the outstanding version with the new physical address. Here, we take advantage of the mapping from logical to physical blocks maintained by the local storage system (Section 5). Though subsequent client operations will be performed on the newest version only, the old versions are kept because they may still be needed for recovering data on other sites.

Next, the delta between the newest and the second newest data versions is sent to all checksum sites in an update request. (Consecutive writes to the same block can be collapsed into one update request unless they straddle a ``sync'' operation. See Section 6.3.) Each checksum site writes the data delta into a free block in its local disk, logs the outstanding version with the address of the delta, and replies to the data site that it is now capable of providing a checksum for the new data version. In addition, since the delta of each data block in the same group is stored independently, the checksum site is capable of computing a new checksum with the old checksum and any combination of the deltas; therefore, invariant 2 is maintained.

Once it receives update replies from all checksum sites, the data site makes the new version the stable version by pointing the logical-to-physical map entry to the physical address of the new version, frees the physical block that holds the old stable version, sends a commit request to each checksum site, and then removes the outstanding version from the log. When it receives the commit request, a checksum site computes the new checksum with the new data delta, writes it on disk, deletes the delta, and removes the outstanding version from the log.

6.1.3  Redo Logs

In order for an update to proceed after temporary site/network outages, we need to maintain for each logical disk on data sites a redo log, indexed by logical addresses. Each entry in the log contains a list of data structures for outstanding versions of the block. Each entry in the list contains the outstanding version number, the physical address, and the status of each checksum site regarding the remote update of this version. The status is ``ready'' if an update reply from the checksum site has been received, or ``pending'' otherwise.

We also need to maintain for each logical checksum disk on checksum sites a redo log, indexed by redundancy group ids. Each entry in the log contains a list of data structures for outstanding data versions in the group. Each entry in the list contains the data site and outstanding version number, and the address where the data delta is stored.

The redo logs, together with other metadata such as the logical-to-physical maps, need to be stored in a permanent storage system that provides higher reliability than those for regular data, since we would like to avoid the cases where the loss of metadata causes surviving data to be inaccessible. The metadata also needs to be cached in memory for fast reads and batched writes to disk. In an ideal configuration, the metadata ought to be cached in non-volatile memory and backed by triple mirroring disks, assuming that regular data is stored on RAID-5 disks.

During each operation, e.g. client read, client write or recovery read, the redo log is always looked up before the logical-to-physical map, so that the newest version is used in the operation.

The redo log will be scanned during a system reboot or a network reconnect. An entry in the log on a data site is created after an outstanding data version is written to disk, and deleted after update replies are received from all checksum sites. Therefore, the presence of such an entry during a system reboot or network reconnect indicates that an update request with the data delta should be resent to all checksum sites with a ``pending'' status. On a checksum site, an entry in the redo log is created after the data delta is written to disk, and deleted after the checksum is recomputed with the delta and stored on disk. Therefore, the presence of such an entry during a system reboot or network reconnect indicates that an update reply should be resent to the data site.

The redo logs can also be used to detect duplicate messages and hence to ensure idempotent updates. Upon receiving an update request with an outstanding version number, a checksum site first checks if the version number already exists in its redo log. If it does, the checksum site learns that it has already committed the data delta, therefore resends an update reply to the data site. Upon receiving an update reply, the data site first looks up the redo log for a corresponding entry. If none is found, the data sites learns that the outstanding version has already been committed locally, therefore resends a commit request to the checksum site. Upon receiving a commit request, a checksum tries to locate a corresponding entry in the outstanding log. If it fails to do, it learns that the version has already been committed, and therefore ignores the request.

6.2  Recovery

Cross-site recovery is initiated when a site loses data that cannot be recovered using local redundancy. The recovered data can be stored either on the same site as the lost data, or on a new site if the old site is destroyed completely. In either case, the site where the recovered data is to be stored serves as the coordinator during the recovery process.

We assume that metadata (e.g., the redo logs and logical-to-physical maps) on both data and checksum sites is stored with high local reliability, such that it will not be lost unless a site suffers a complete disaster. We do not attempt to recover metadata from remote sites. In the event of a site disaster, we rebuild metadata from scratch.

In the beginning of a recovery process, the coordinator determines the logical addresses of the data blocks to recover. If a site loses some storage devices but not the metadata, it can determine the addresses of blocks on the lost devices by scanning its logical-to-physical map. If a site is completely destroyed, all blocks in the address range from 0 to the capacity of the lost logical disk need to be recovered.

To reconstruct a lost data block d_i, the coordinator first determines which checksums (identified by a version vector) from surviving checksum sites and which data versions from surviving data sites to use. Then, the coordinator requests those versions and compute the lost data.

The version vector is determined in the following way. The coordinator requests the newest version numbers of the lost block d_i from surviving checksum sites, and the stable version numbers of other blocks in the same group from surviving data sites. (Such requests are referred to VersionRequest below.) If k data blocks in the group are lost, the newest recoverable version of block d_i is the one for which at least k checksum sites are capable of providing a consistent checksum. It is guaranteed that at least one such version, i.e. the stable version, exists as long as k checksum sites survive (Section 6.1.1). (If fewer than k checksum sites survive, recovery is simply impossible under the given encoding.) The stable versions of other data blocks in the group are also guaranteed to exist. The coordinator requests the explicit stable version numbers from data sites because the checksum sites may transiently have an old stable version and consider the new stable version to be outstanding still.

The version vector of the checksums consists of the newest recoverable version of the lost block d_i and the stable versions of other data blocks. Upon replying to a VersionRequest, a surviving site temporarily suspends the commit operations for the block involved. This way, the version selected by the coordinator will still be available by the time it is requested in the second step. Client writes and remote updates of the involved block are not suspended; only the deletion of the old stable version is postponed.

Once the version vector is determined, the coordinator requests the selected data versions and checksums from the surviving sites, reconstructs the lost data block from the returned blocks, and writes it onto a local disk. After sending the requested block, each surviving site can resume the commit operations for that block. If the data reconstruction did not complete for any reason, e.g. the coordinator crashes, a re-selection of version vector is necessary.

Finally, the coordinator attempts to synchronize all checksum sites with the recovered data version, i.e. to commit the recovered version and to delete other (older or newer) versions if there are any. The coordinator uses the redo log to ensure eventual synchronization in the face of site/network outages.

The protocol described above is for the recovery of a data block. The recovery of a checksum block is similar, with small variations in the determination of group numbers, in the selection of data versions and in the final synchronization. We omit the details here in the interest of space.

6.3  Serialization of Remote Updates

We need to ensure that consecutive writes to the same data block are committed on both data and checksum sites in the same order as the write operations return to clients. This can be done by sending the update and commit requests for the same block in the ascending order of their version numbers.

Applications sometimes need explicit serialization of writes as well. For example, a file system may want to ensure that a data block is written before its inode is updated to point to the block. In the presence of buffer caches in storage systems, the serialization needs to be done via a ``sync'' bit in a block write request or a separate ``sync'' command (e.g. the SYNCHRONIZE CACHE operation in SCSI-2 [13]); both sync requests cause specified blocks to be flushed from cache to disk before the requests are completed. It is required that writes issued after a sync request are perceived to take effect after the sync request does, in the face of system crashes.

Unfortunately, it may not be practical to require that remote checksums be committed as well before a sync request is completed. The long latency in WAN communication may be unacceptable to certain applications. If a checksum site is unreachable, the sync could be delayed indefinitely.

Therefore, we relax the semantics for sync requests in the cross-site redundancy context for better performance and availability. In our system, a sync request is completed after the requested data has reached local storage, but before its delta reaches the checksum sites. In order to prevent inconsistency upon recovery caused by out-of-order writes, we guarantee that writes following a sync request are propagated to the checksum sites only after the data in the sync request has been committed on the checksum sites. Therefore, we can collapse the update requests for consecutive writes to the same data block and propagate them as one request only if those writes are between two consecutive sync operations.

The serialization during a redo process after a system crash or network outage can be enforced by resending update requests in the ascending order of version numbers. This indicates that version numbers of all data blocks on the same logical disk need to be serializable.

We do not attempt to guarantee cross-site serialization because Myriad is designed for independent applications per site (Section 2).

6.4  Performance Implications

A client write operation involves a single disk write of the new data and a few updates to the metadata in non-volatile memory; therefore, we do not expect the client to observe significant increase in write latency. A complete remote update requires the following additional operations on the data site: a disk read, an xor operation and several updates to the metadata in non-volatile memory. It also requires the transmission of a block over the WAN, and the following operations on each checksum site: a disk read, a checksum computation, two disk writes, and several updates to the metadata in non-volatile memory. Therefore, for a Myriad system with n data sites, the write bandwidth on each data site is limited by the minimum of the following: data site disk bandwidth divided by 2, WAN bandwidth, and checksum site disk bandwidth divided by 3. We expect the WAN bandwidth to be the limiting factor.

The consumption of WAN bandwidth in our scheme is comparable to that of a mirroring scheme able to survive the same number of site losses. As Figure 6 shows, if there are k checksum sites, for each logical block written, an update request with the delta (of the size of a block) is sent k times, once to each checksum site. A system with k remote mirrors would also require sending a newly written block of data k times, once to each mirror site. We also send k commit requests and expect a mirroring scheme to do the same if it also uses two-phase commit to guarantee cross-mirror consistency. Similar optimizations (e.g., collapsing consecutive writes to the same block) can apply in both cases.

6.5  Storage Overhead

As discussed earlier in this section, we need a logical-to-physical map for each logical disk on data sites. There is an entry in the map for each logical data block, and the map is indexed by logical block address. Each entry in the map contains the physical address of the stable version, and the stable version number. We also need a logical-to-physical map for each logical disk on checksum sites. There is an entry in the map for each redundancy group, and the map is indexed by group id. Each entry in the map contains the physical address of the checksum block, and the stable version numbers of data blocks in the group.

Assume that each redundancy group consists of n data and m checksum blocks. For every n data blocks, the storage required for the map entries is n ×(sizeof(paddr) + sizeof(vernum)) bytes on the n data sites, and m ×(sizeof(paddr) + n ×sizeof(vernum)) bytes on the m checksum sites. Therefore, the overall storage overhead for the maps is (1+[ m/n]) ×sizeof(paddr) + (1+m) ×sizeof(vernum) bytes per data block. For example, with n = 3, m = 2, sizeof(paddr) = 4 bytes, and sizeof(vernum) = 4 bytes, it would amount to 18.7 bytes per data block. The storage overhead for the maps is roughly 0.028% for a block size of 64 KB and 0.45% for a block size of 4 KB.

We expect the maps to be much larger than the redo logs because the latter contains only blocks ``in transition''. The number of such blocks depends on the burstiness of client writes and on the difference between the local disk bandwidth and the WAN bandwidth.

7  Related Work

Myriad is most related to the distributed RAID algorithm proposed by Stonebraker and Schloss [19]. Like Myriad, they envision independent local storage systems on geographically separate sites protecting one another's data with a redundancy scheme other than mirroring. However, a key difference is that their redundancy groups consist of physical blocks while Myriad's consist of logical blocks. Physical blocks are overwritten in place by client and redundancy update operations. Thus, redundancy groups could become inconsistent, though their recovery procedure can detect this and retry. Also, local write latency is roughly doubled because a local write cannot return until after the old data are read (to compute the delta) and subsequently overwritten with the new data. Myriad avoids these by forming redundancy groups with logical blocks that may have multiple versions coexisting simultaneously. During a redundancy update, the old versions of data and checksum are not affected and remain consistent. And a local write can return immediately after a single I/O (to write the new data version); the old data can be read and the delta computed later.

Striped distributed file systems such as Swift [15], Zebra [11] and xFS [20,3] are related to Myriad in that they also keep data and parity blocks on multiple storage servers. However, they have different a technology assumption, goal, and hence data layout. They are designed for servers connected by a high-performance LAN, while in our case servers are connected by a (relatively) low-performance WAN. Since the LAN has low latency and high bandwidth, these systems stripe the data blocks in a file across servers to maximize read/write bandwidth via server parallelism. For Myriad, since moving data over a WAN is slow, related data reside on the same site and client accesses are always local. Checksum blocks are computed from unrelated data blocks on different sites only for disaster tolerance.

TickerTAIP is a disk array architecture that distributes controller functions across loosely coupled processing nodes [4]. It is related to Myriad in that multiple nodes cooperate to perform a client write and the corresponding parity update. TickerTAIP uses a two-phase commit protocol to ensure write atomicity, and proceeds with a write when enough data has been replicated in more than one node's memory. After a node crashes and reboots, the replicated data can be copied to that node so that the operation will complete eventually. Myriad commits the write when sufficient data has been written to permanent storage so that each site can join a consistent group upon crash and reboot without requesting data from other sites first. The difference results from our attempt to avoid as much as possible WAN communications. In another respect, TickerTAIP preserves partial ordering of reads and writes by offering an interface for each request to explicitly list other requests that it depends on. It then manages request sequencing by modeling each request as a state machine. Myriad also attempts to preserve partial ordering on the same site, but only using standard interfaces, e.g. the SYNCHRONIZE CACHE operation in SCSI-2 [13]. All reads and writes following a sync operation implicitly depend on that operation. No cross-site sequencing is supported because Myriad is designed for independent applications per site. As a result, the management of sequencing in Myriad is much simpler than that in TickerTAIP.

Aspects of Myriad's design use classic techniques widely used elsewhere. In Myriad, clients access blocks using logical addresses, while the storage system decides which physical block(s) actually contain the data. We exploit this logical-physical separation to keep physical blocks of data and checksums consistent during redundancy updates. It has been used for many other purposes: in Loge to improve disk write performance by allowing new data to be written to any convenient location on a disk surface [9], in Mime to enable a multi-disk storage subsystem to provide transaction-like capabilities to its clients [5], in Logical Disk to separate file management from disk management and thus improve the structure and performance of file systems [6], and in the HP AutoRAID hierarchical storage system to allow migration of data between different RAID levels (namely RAID-1 and RAID-5) in a way transparent to clients [21].

Like AFRAID [17], Myriad trades a small window of data vulnerability for write performance. Specifically, Myriad updates remote redundancy information after the client write has returned. We make this design choice because client writes would otherwise be too slow. In exchange, the newly written data will be vulnerable to a site disaster before the update is completed. However, other (previously written) data blocks in the same group are not affected because we do not update in place and so the old data and checksum versions remain consistent. In contrast, the AFRAID disk array design physically overwrites data blocks without parity updates, leaving the group inconsistent until the parity block is recomputed later. Before that, all data blocks in the group are vulnerable to a single-disk failure. We prefer not to take a similar risk in Myriad. If we did, each site might always have some blocks that are not protected from disaster simply because other blocks (on other, separately operated sites) in the same redundancy group have just been written by their local clients and the corresponding redundancy updates are in progress. Moreover, to recompute the checksum block(s) as AFRAID does, Myriad would have to send all the data blocks in the group to the checksum site(s) and to carefully orchestrate the recomputation as an atomic operation. These are much more expensive and complex in a WAN-connected distributed system like Myriad than in a disk array with a centralized controller like AFRAID.

8  Conclusions and Future Work

The usual approach to ensuring that data in a geoplex survives site failures is to mirror the data. We have presented early results of our study in using erasure codes across sites as an alternative. Our motivation is to reduce the cost of providing data disaster tolerance while retaining much of the reliability. Our results thus far indicate that the TCO for the storage system can be reduced by 20-25% (relative to mirroring) while providing reliability far beyond a non-disaster-tolerant system. We also present a protocol for updates and recovery in a redundancy scheme based on erasure codes. Our scheme makes sense under the system and application assumptions in Section 2, although these are less general than for mirroring.

While the related idea of software RAID has been studied in various contexts, we believe that our approach is novel. In essence, we combine unrelated data blocks at different sites into redundancy groups that protect the data of their members. We assume that the data sites provide a logical disk interface to their client applications. This simplifies our protocol design by using multiple data versions instead of overwriting data blocks in place, making recovery much less error-prone.

There are several interesting future directions. While static block grouping is simple, a more dynamic scheme may offer more flexibility for site configurations. It involves maintaining maps of group ids to the logical data blocks each group consists of. Also, we would like to have a systematic proof for the correctness of the update and recovery protocol. Finally, since we use shadow paging, for now we can only exploit sequential disk access within a block. So we want a relatively large block size, which in turn makes the solution less general. It may be worthwhile to explore alternatives that rely on intelligent physical placement of data blocks.

9  Acknowledgments

References