- (i)
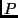 is a finite set of control locations;
is a finite set of control locations;
- (ii)
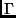 is a finite set of stack symbols;
is a finite set of stack symbols;
- (iii)
-
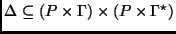 is a finite set of rewrite rules of the shape
is a finite set of rewrite rules of the shape
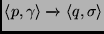 .
.

Pushdown systems provide a natural execution model for programs with recursion. They form a well-studied class of infinite-state systems for which many important problems like equivalence checking and model checking are decidable [4].
The set
![]() are the configurations of
are the configurations of ![]() .
If
.
If
![]() is a rewrite rule of
is a rewrite rule of
![]() , then for each
, then for each
![]() the configuration
the configuration
![]() is an immediate successor of the configuration
is an immediate successor of the configuration
![]() . A run of
. A run of ![]() is a sequence
is a sequence
![]() ,
such that for all
,
such that for all ![]() ,
,
![]() is an immediate
successor of
is an immediate
successor of
![]() .
.
We now define how a set of methods ![]() induces a PDS.
induces a PDS.

The rewrite rules of the
pushdown system can be interpreted
as simply manipulating the calling stack
of the program from which the PDS was obtained.
Given a configuration
![]() let
point
let
point ![]() .
.