Method Call Graphs

The methods $M$ are partitioned into classes $C$, which are themselves partitioned into packages $P$. We assume the usual Java naming conventions with fully qualified names, i.e., a class has a name $\mathit{Package.identifier}$ and a method has a name $\mathit{Class.identifier}$.

Definition 1 (Method Graph, adapted from [13])   A method graph is a tuple

$$m \;\stackrel {\Delta}{=}\; \left(V_m, \rightarrow_{m} , \lambda_m, \mu_m \right)$$

such that:

(i)

$V_m$ are the program points of $m$,

(ii)

$\rightarrow_{m} \subseteq V_m \times V_m$ are the transfer edges of $m$, and

(iii)

$\lambda_m : V_m \rightarrow T$ designates to each program point of $m$ a program point type from the set $T \;\stackrel {\Delta}{=}\; \{$entry$,$   seq$,$   call$,$   return$\}$.

(iv)

$\mu_m: V_m \rightarrow \wp(M)$ designates to each program point of type call of $m$ a non-empty set of methods.

We assume the program point sets $V_m$ to be pairwise disjoint. The program points of the program is the set $V \;\stackrel {\Delta}{=}\; \bigcup_{m \in M} V_m$.

The program point type indicates whether (entry) a node is the entry point of a method, (seq) a node in which no method call or return takes place, (call) a node from which a method call takes place, or (return) a node in which the execution of the method finishes and control flow returns to the calling method.

For convenience, we introduce the predicates

$$\begin{array}{rcl} v : t &\stackrel {\Delta}{=}& \lambda_m(v... .... \;v : \mbox{\sf class } c \;\wedge \; c \in p\\ \end{array}$$

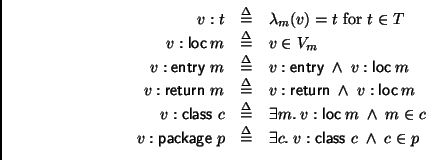
We further define a predicate $v : \mathsf{api}$, which holds if the program point $v$ occurs in a method in a JavaCard API package (for standard JavaCard this corresponds to one of java.lang, javacard.framework, javacard.security or javacardx.crypto).