


Next: Randomness Used Inside the
Up: Pseudo Random Number Generators
Previous: arc4random(3)
In OpenBSD, we designed a non-repeating pseudo-random number generator
that was very fast and did not require additional resources.
For 16-bit non-repeating numbers, we used a prime 214 < p <
215 and g a randomly chosen generator for 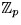 . Being
a generator, g has the property that any value 0 < x < p can be
generated as
. Being
a generator, g has the property that any value 0 < x < p can be
generated as 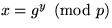 , for some value y.
, for some value y.
We then pick random a, b and m with 214 < m < 215 so that
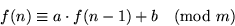
becomes a linear congruential generator (LCG).
We then determine the actual ID as
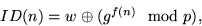
where w is a random seed. After the linear congruential generator
has been exhausted, the most significant bit in ID(n) is toggled and
all parameters g, a, b, m, and w from above are chosen anew.
Because the linear congruential generator does not repeat itself and a
new number space is chosen after reinitialization, the generated IDs
do not repeat themselves. The PRNG is typically seeded with material
from the kernel randomness pool.
& D. Keromytis
4/26/1999

![]() . Being
a generator, g has the property that any value 0 < x < p can be
generated as
. Being
a generator, g has the property that any value 0 < x < p can be
generated as ![]() , for some value y.
, for some value y.
![]()
![]()