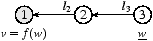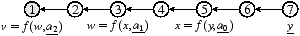NetComplex: A Complexity Metric for Networked System DesignsByung-Gon Chun, ICSI;
Sylvia Ratnasamy, Intel Research Berkeley;
Eddie Kohler, UCLA |
Abstract: The systems and networking community treasures
“simple” system designs, but our evaluation of system simplicity
often relies more on intuition and qualitative discussion than
rigorous quantitative metrics.
In this paper, we develop a prototype metric that seeks to
quantify the notion of algorithmic complexity in
networked system design.
We evaluate several networked system designs through the lens of
our proposed complexity metric and demonstrate that our metric
quantitatively assesses solutions in a manner compatible with
informally articulated design intuition and anecdotal evidence
such as real-world adoption.
1 Introduction
The design of a networked system frequently includes a strong
algorithmic design component. For example, solutions to a variety of
problems – routing, distributed storage, multicast, name
resolution, resource discovery, overlays, data processing in sensor
networks – require distributed techniques and procedures by which
a collection of nodes accomplish a network-wide task.
Design simplicity is a much-valued property in such systems.
For example, the literature on networked systems often refers
to the importance of simplicity (all emphasis added):
-
- The advantage of Chord is that it is substantially less complicated…(Chord [35])
- This paper describes a design for multicast that is simple to understand…(Simple Multicast [32])
- This paper proposed a simple and effective approach…(SOSR [17])
Likewise, engineering maxims stress simplicity:
-
- All things being equal, the simplest solution tends to be the right one. (Occam’s razor)
- KISS: Keep It Simple, Stupid! (Apollo program)
However, as the literature reveals, our
evaluation of the simplicity (or lack thereof) of design
options is often through qualitative discussion or, at best,
proof-of-concept implementation. What rigorous metrics we do employ
tend to be borrowed from the theory of algorithms. For example,
two of the most common metrics used to calibrate system designs
are the amount of state maintained at nodes and the number
of messages exchanged across nodes.
These metrics,
however, were intended to capture the overhead or efficiency of an
algorithm and are at times incongruent with our notion of simplicity.
For example, flooding performs poorly on the number of messages
exchanged across nodes, but
most of us would consider flooding a simple, albeit inefficient, solution.
Similarly, a piece of state obtained as the result of a distributed
consensus protocol feels intuitively more complex
than state that holds the IP address of a neighbor in a wireless
network.
We conjecture that this mismatch in design aesthetic contributes to
the frequent disconnect between the more theoretical and applied
research on networked system problems. A good example of this is the
work on routing. Routing solutions with small forwarding tables are
widely viewed as desirable and the
search for improved algorithms has been explored in multiple
communities; for instance, a fair fraction of the proceedings at STOC,
PODC, and SPAA are devoted to routing problems. The basic
distance-vector and link-state protocols incur high routing state
(O(n) entries) but are simple and widely employed. By contrast, a
rich body of theoretical work has led to a suite of compact
routing algorithms (e.g., [10, 3, 36, 2]).
These algorithms construct optimally small routing tables (O(√n) entries) but appear more complex and have seen little adoption.
This is not to suggest existing overhead or efficiency metrics are
not relevant or useful. On the contrary, all else being equal,
solutions with less state or traffic overhead are strictly more
desirable. Our point
is merely that design simplicity plays a role in selecting solutions for
real-world systems, but existing efficiency or performance-focused metrics
can be misaligned with our notion of what constitutes simple system designs.
This paper explores the question of whether we can identify complexity
metrics that more directly capture the intuition behind our judgment
of system designs.
Because the system designs we work with are fairly well-specified,
we believe there is no fundamental reason why our
appreciation of a design cannot be reinforced by quantifiable measures.
Such metrics
would not only allow us to more
rigorously discriminate between design options, but also
to better align the design goals of the theory and systems communities.
We start by reporting on a survey we conducted to understand how system designers
evaluate and articulate complexity in system design (Section 2).
Building on this, we define a complexity metric in
Sections 3 and 4
and evaluate several networked system designs through the lens of our
complexity metric in Section 5.
Using this analysis, we demonstrate that our metric quantitatively
differentiates across flavors of solutions and ranks systems in
a manner that is congruent with our survey.
We discuss the limitations of our metric
in Section 6, review related work in Section 7,
and conclude in Section 8.
Finally, it is important to clarify the scope of our work.
We intend for our complexity metric to complement – not replace –
existing efficiency or performance metrics. For example,
in the case of a routing algorithm, our metric might capture the
complexity of route construction but reveal little about
the quality of computed paths. In addition, while we
focus on system design at the algorithmic or procedural level, there
are many aspects to a software system that contribute to its ultimate
complexity. For example, as the CAP theorem [13] tells us,
the careful selection of a system’s service model
profoundly impacts complexity. The same is true for the
sound design of its software implementation. Although at least as
important as distributed complexity, these are not aspects we
consider in this paper.
Lastly, we stress that we view our metric as a prototype:
one specific metric that works well with several classes of important
systems. We expect that the best-suited metric
will emerge in time after much broader discussion and evaluation (similar
to the development of standard benchmarks in many communities such
as databases and computer architecture).
As such, we view our contribution primarily in getting the ball rolling
by providing a candidate metric and set of results for further scrutiny.
2 Perceived Complexity
We conducted a survey to explore how system designers perceive
complexity of networked system algorithms such as routing,
distributed systems, and resource discovery.
Nineteen students in a graduate distributed systems class at UC Berkeley
participated in the survey.
Participants were asked to rank which of two comparable networked system
algorithms they viewed as more complex on a scale where 1 means
system A is far more complex and 9 means B is far more complex.
Participants were also asked to rationalize their choice in 2–3 sentences.
We discuss the algorithms we surveyed in detail in the later sections of
this paper;
Table 1 briefly summarizes the findings from the
survey’s quantitative ranking.
The one-sample t-test reveals that participants consider distance vector (DV)
routing as more complex than link state (LS) routing
but less complex than landmark or
compact routing. In evaluating classical distributed systems,
participants viewed solutions such as quorums, Paxos, multicast, and atomic
multicast as more complex than read-one/write-all, two
phase commit, gossip, and repeated multicast, respectively.
Napster was perceived as simpler than Gnutella and
systems such as Gnutella and the Domain Name System (DNS) as simpler
than distributed hash tables (DHTs).
| | | More complex |
| Algorithm A | Algorithm B | algorithm |
|
| DV | LS | A | | (p < .060) |
| DV | Landmark | B | | (p < .050) |
| DV | Compact | B | | (p < .030) |
| DV | RCP | not significant |
|
| Read one/write all | Quorum | B | | (p < .007) |
| Two phase commit | Paxos | B | | (p < .001) |
| Gossip | Multicast | B | | (p < .013) |
| Atomic multicast | Repeated multicast | A | | (p < .001) |
| Locking | Lease | not significant |
|
| Napster | Gnutella | B | | (p < .001) |
| DHT | Gnutella | A | | (p < .020) |
| DNS lookup | DHT lookup | B | | (p < .007) |
| Table 1: Survey results on comparing networked systems complexity.
For each question, we present which algorithm was statistically rated
as more complex based on the t test’s p-value, which indicates the
probability that the result is coincidental. The smaller the p-value,
the more significant the result. |
The rationales for these rankings
shed more insight. Participants found a system
was complex if it was hard to “get right,” understand,
or debug, or if it could not easily cope with failures. For the most part, issues of
scalability or performance did not figure in their responses.
Some sample answers include: “components have complex interactions,”
“centralized or hierarchical is simpler than decentralized,”
“structure is complex,” and
“requires complex failure and partition handling.”
Tellingly, participants at times could not clearly articulate why one
algorithm was more complex than the other and resorted
to circular definitions – e.g., “chose system A because it is more
complicated” or “B’s protocol is more complex.”
3 Components of Complexity
A complexity metric could make these arguments objective. A good metric
would be based on quantifiable, concrete measurements of the system
properties that induce implementation difficulties, complex interactions
and failures, and so forth.
Many metrics are possible. A perfect metric would be intuitive and easy to
calculate, and would correlate with other, more subjective metrics, such as
lines of code or system designers’ experience.
We build on the observation that much of system design centers on
issues of state – the required state must
be defined and operations for constructing and using it must be developed
–
but in distributed systems, one state can derive from states stored on
other nodes.
To calculate its state, a node must hear from the remote nodes that store
the dependencies. This adds additional dependencies on the network and intermediate
node states required to relay input states to the node in question.
Thus, not only are a given piece of state’s dependencies distributed, there are
also more of them.
We conjecture that the complexity particular to
networked systems arises from the need to ensure state is kept in sync
with its distributed dependencies. The metric we develop in this paper
reflects this viewpoint and we
illustrate several systems for which this dependency-centric approach
appears to appropriately reflect system complexity.
Alternate approaches are certainly possible however – e.g., based on
protocol state machine descriptions, a protocol’s state space, and
so forth – and we leave a comprehensive exploration
of the design space for metrics and their applicability to future work.
Our goal then is to derive a per-state measure cs that
captures the complexity due to the distributed state on which a state s
depends.
While a natural option would be simply to count s’s
dependencies,
this is not
sufficiently discriminating: dependencies, like state, can vary greatly
in the burden they impose.
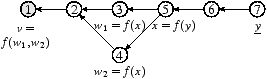
Consider Figure 1, which shows dependency relationships between
states for several simple networks.
In Fig. 1b, a simple distribution tree, v is
computed from three dependencies w, x, and y,
while in Fig. 1c, which transforms a
value over several hops,
v (e.g., the distance from node 1 to node 7)
has just one direct dependency w, which is
computed from a1 and x, which is in turn
computed from y and a0.
However, a change in y in Fig. 1b
will affect only v, while the same change in
Fig. 1c must propagate through x and w
first. As a system, we argue that Fig. 1c is more
complex than Fig. 1b.
We therefore weight each state, and instead of naively counting
dependencies, calculate a state’s complexity by summing the
complexities of its dependencies.
The sum includes not only direct dependencies on values, but also
dependencies on the transport states required to relay those values,
accounting for networks whose transport relationships are expensive to
maintain.
Some flexibility is required to account for the different types of
dependencies in real networked systems, including redundancy, soft state,
and so forth, and to differently penalize transport and value dependencies.
Nevertheless, our metric is defined exclusively by counting; we
avoid incorporating intricate probabilistic models of node or link behavior
or state machine descriptions and the like.
This keeps our metric usable, lending it to evaluation through simple
examination and analysis or even empirical simulation,
and represents one particular tradeoff between a metric’s discriminative
power and the simplicity of the metric itself.
Some of the limitations of our counting-based approach are discussed
in Section 6.
4 A Complexity Metric
Given a system that consists of a set of states S, our goal is to assign
a complexity metric cs to each state s ∈ S.
We write states as lowercase letters, such as s, v, and w. Where the
context is clear, we abuse notation and merge the identities of states and
nodes; e.g., instead of “delivered to node 1, which stores state x,”
we simply say “delivered to x.”
Local or primitive state can be maintained without
network traffic, as in a sensor node’s temperature reading. We sometimes
indicate primitive state with an underline, as in w.
All other state is derived at least partially from states held at
other nodes.
We call these remote states direct value dependencies.
In Fig. 1a, w is a primitive state, and
v is a derived state with one value dependency, namely w,
as indicated by the definition v = f(w).
Primitive state is assigned zero complexity, while any derived state has
positive complexity.
The set of state s’s direct value dependencies is written Ds.
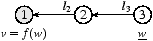 |  |
| (a) Collecting one value | (b) Collecting several values |
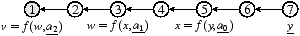
(c) Collecting an aggregate value

(d) Collecting one value via intermediate states
(e) Collecting via branches forked and then merged
| Figure 1: State relationships in five toy scenarios. For
clarity routing table state, written l, is only shown in scenario (a). |
A derived state also depends on the transport state required to relay value
dependencies through the network.
For instance, in Fig. 1a,
propagating w to v uses the l2 and l3
routing table entries at nodes 2 and 3, respectively.
We call these states transport dependencies and account for their
complexity.
The set Ts ← x is defined as the set of transport dependencies
involved in relaying x’s value to s; it is empty when
x ∉ Ds.
In terms of maintaining state consistency, transport dependencies
are less of a burden than value dependencies since changes in a
state’s transport dependencies do not induce costs to keep that state in sync
and, as we shall see, our metric reflects this.
For instance, in Fig. 1a, any change in w must be
communicated to node 1, but a change in l2 need
not, since v depends on the l states only for the
delivery of w.
While some value dependencies require state changes be relayed, others need
only be established once.
For example, if v were defined as a function of w
at some specific time, rather than of w’s
current value, then once established v is unaffected by
changes elsewhere in the network. We say that
state x and one of its value dependencies y are linked if a
change in y must be propagated to x, and unlinked otherwise.
Linked value dependencies are the major source of network complexity due
to the state maintenance they incur and are treated accordingly
by our metric.
Evaluating the metric requires determining dependencies among states and
defining which dependencies are linked or unlinked.
Unused or redundant dependencies, which frequently occur, can be
measured in several ways.
For example, consider Fig. 1b, where
v=f(w, x, y) and let us assume that
the value v takes at any point is based on just one of its inputs
(for instance, perhaps the active input is chosen based on minimum path length).
Then v’s value dependencies have distinctly different importance:
ensuring consistency requires that v and its active input stay synchronized,
while updates from the other dependencies are less critical.
When we consider dependencies of state v, we focus on
these active states that derive v and ignore unused value dependencies.
We now turn to the metric itself, first defining a submetric us
which we call the value dependency impact. us
measures the number of remote states on which s is value dependent
directly or indirectly. Stated otherwise, these are primitive states that,
if they were to change, could result
in an update at s and hence one can intuitively view us as
indicative of the number of updates seen at s for
maintaining consistency with its value dependencies.
us is defined mutually recursively with us ← x,
which measures the number of states on which s is value dependent
via some direct value dependency x ∈ Ds. For local state s,
we have Ds = ∅, us = us ← x = 0.
|
| | us | | | | | | | | | | |
|
us ← x | | = | ⎧
⎪
⎪
⎨
⎪
⎪
⎩ | | ux | if x is linked to s and |
| | x is not dependent on local state, |
| ux + 1 | if x is linked to s and |
| | x is dependent on local state, |
| є | if x is unlinked to s. |
|
|
| | | | | | | | | |
|
If the dependency s ← x is linked, s must be notified of
any change in x ∈ Ds. Applied recursively, changes in any of
x’s direct or indirect
value dependencies must also be passed on to s. Thus,
the number of dependencies inherited via x is x’s own value
dependency impact, ux, plus one in the event that x was
derived (in part) from local state (since a change caused by state
local to x would not be accounted for in ux).
For example, states w and x in Fig. 1d,
do not include any local inputs while the same states
in Fig. 1c do.
If s is unlinked to x, then any changes in
x are not propagated to s, so we cut off x’s value dependency impact.
However, to ensure that s is charged for its initial reliance on x, we
introduce є, 0 < є ≪ 1, and charge this amount for
every non-local, unlinked dependency.
Note that our definition of us assumes the dependencies s
inherits are independent – a simplifying assumption due to which
us overcounts in some dependency structures.
For example, in Fig. 1e, if
v ← {w1,w2} ← x ← y, then y is
counted twice in uv, once via w1 and once via w2.
This situation arose rarely. Many such branching dependency structures
represent unused or redundant dependencies that we model by picking one
active input, which leaves the dependency graph in the form of a tree.
The complexity of s is then defined as follows:
|
| | cs | | | | | | | | | | |
|
cs ← x | | = | ⎧
⎪
⎪
⎨
⎪
⎪
⎩ | | if x linked, |
| є | if x unlinked. |
|
|
|
| | | | | | | | | |
|
This definition accounts for the entire
scaffolding of distributed dependencies that maintain changes from s’s
dependencies to s itself.
Suppose s’s direct value dependencies are all linked. Then,
the first term ∑x∈ Ds us ← x (=us) is
s’s value dependency impact.
The second term ∑x∈ Ds ∑y∈ Ts ← x
max(cy,є) accounts for the complexity of the transport states from
s’s direct value dependencies to s itself; є again ensures that all
links are counted, here including transport links that nominally require no
state (such as one-hop wireless broadcast).
Finally, the last term ∑x∈ Ds cx covers the complexity from
inherited (transport and value) dependencies downstream from x.
Local state s has cs = 0.
Thus intuitively, where us was indicative of the updates seen at s, cs
is indicative of the updates seen across all states – value and transport –
that maintain changes from s’s dependencies to s.
For a chain of linked dependencies from x0 to xi (Fig. 1c),
which depends on its local state ai
(perhaps xi measures
node i’s hop count to node 0), and writing ci for cxi and so
forth, we have ui = i and
Ignoring transport dependencies, the result is ci =
(i2+i)/2: chained linked dependencies induce complexity proportional to
the square of the length of the chain.
In Figure 1, if we assume all l states have
complexity t, the metric yields cv=1+2t in
Fig. 1a, cv=3+6t in Fig. 1b,
and cv=6+6t in Fig. 1c.
We sometimes convey intuition about the sources of complexity
by writing cs = csV + csT, where csV is the
complexity contributed by value dependencies and csT is the
complexity contributed by transport dependencies:
|
| | cs ← xV | = us ← x + cxV , | | | | | | | | | |
|
cs ← xT | | | | | | | | | | |
|
This split is purely for illustration and does not affect the definition of
complexity in any way.
To measure the complexity of an operation, such as name resolution,
routing, agreement, replication, and so forth, we simply measure the
complexity of a state created or updated by that operation. For example,
to measure the complexity of multihop routing, we imagine a piece of state,
s, derived from one primitive value dependency, x, whose value must be
routed across a multihop network. The complexity of routing is defined as
cs, which accounts for the multihop transport
dependencies used to route x across the network.
Assuming a network with diameter d where every routing table entry
has complexity cr, the resulting complexity is O(dcr).
This paper evaluates different networked system
designs by comparing their complexities for specific operations of
interest (e.g., route, write_object,
find_object). We found it sufficient to consider one operation at a
time for our evaluation. If desired, one might (for example)
select the average complexity of key operations as the overall complexity
of the networked system. We proceed to evaluating the above metric and
defer a discussion of its scope and limitations to Section 6.
4.1 Some Canonical Scenarios
We first examine how the above complexity metric fares in evaluating
a few simplified network scenarios and in the following section
explore a suite of more complete networked system
solutions. Before this, we first introduce two conditions that appear
repeatedly in our analysis of system designs and are hence worth
calling out.
Redundant inputs and paths
Many systems build in redundancy to achieve higher robustness. In
our analysis, this manifests itself as some state s that
has multiple inputs or paths but only a subset of them
are needed to derive s (akin to our discussion of active value
dependencies in the previous section). For example, a multiple input
scenario could be a node trying to discover the address of a
wireless access point (AP) – the node listens for AP beacons
but need only hear from a single AP to establish connectivity state.
An example involving redundant paths might include two data centers
that provision multiple disjoint network paths between them. When
a message is encoded with (m,k) erasure code and each code
is sent to a distinct path, the destination can construct the message if
any k out of m paths work correctly.
We call this the k-of-m scenario where m is the total
number of inputs (paths) available and k is the number of inputs (paths)
required.
We define the complexity of s derived from k-of-m inputs as
being k times the average complexity due to a
single input. As shown in [9], this
average can be computed simply as 1/m times
the complexity of s assuming all m inputs were required inputs.
Likewise, for the multipath scenario in which a single input x can be
relayed to s using any k of m available paths, we calculate
the complexities due to the transport states between x and
s as k times the average complexity due to the transport
states along any one path.
Recursion
In some systems, a piece of state s is derived by an operation that
uses states that were themselves set up by the same operation.
For example, in DHTs, a node discovers its routing table entries
using a lookup operation that makes use of state (at other nodes)
that was itself set up using lookup operations.
We use two complexity computation passes for
state that involves this kind of recursion.
In the first pass, we compute the complexities from value
and transport dependencies with the assumption that states
used by the operation do not depend on the operation.
We compute the final complexities in the second pass in terms of
an operation on states whose complexities are computed in the
first pass. In Section 5, DHTs and
Paxos are canonical examples that involve recursion.
| Figure 2: Canonical scenarios. For clarity we do not show the local and
transport state at each node. In all scenarios other than (1) and (2), the
transport state is assumed to have complexity t. |
Canonical scenarios
We recap the following canonical scenarios, also depicted
in Figure 2. In many cases, we can construct dependency
structures of networked system algorithms by composing several
canonical scenarios. In all scenarios other than (1) and (2), we assume
that the transport state at each node has complexity t.
(1) single input, 1-hop broadcast: here s is derived by listening to
the broadcast of x. We assume x is local state and hence cx=0. Moreover,
the complexity of transport state at x equals zero since broadcasting does
not require any non-local transport state to be established at x.
Correspondingly, state s has complexity cs=1+cx + max(0,є) =
1+є.
(2) single unlinked input, 1-hop broadcast:
this case is identical to the previous case but here s is unlinked to x (e.g., s
stores the value of x as soft-state) and hence us ← x=є and cs=є.
(3) single input, 1-hop unicast: this is identical to the first case, except that instead of broadcasting, x is routed to s using transport
state at x which has complexity t and hence cs=1+t.
(4a) single input, 1-of-m paths: this is identical to the previous case but we now have m identical paths from x to s. As before, the complexity of the transport state for each path is t and hence cs=1+t.
(4b) single input, k-of-m paths: this is identical to the previous case
but here x must be delivered to s along k paths and hence cs=1+kt.
(5a) 1-of-m inputs, single path per input: 1 input
must be delivered to s and hence cs=1+t.
(5b) k-of-m inputs, single path per input: similar to the
previous case but here k inputs must be delivered to s and
hence cs=k(1+t).
(6) m value dependencies; 1 direct, m−1 indirect: similar to
Fig. 1c,
here the value of each xi is computed from
that of xi+1 and local state and hence us=m and cs=m(m+1)/2+mt.
(7) m direct value dependencies: similar to
Fig. 1b, s is computed from m inputs each of which
is directly connected to s and hence cs=m(1+t).
(8) tree: each intermediate node has two children and the
tree height is O(logm). Hence cs = O(m logm + mt).
| Scenario | cs |
|
| (1) 1 input, 1-hop broadcast | 1+є |
| (2) 1 non-value-dependent input, | є |
| 1-hop broadcast | |
| (3) 1 input, 1-hop unicast | 1+t |
| (4a) 1 input, 1-of-m paths | 1+t |
| (4b) 1 input, k-of-m paths | 1+kt |
| (5a) 1-of-m inputs, 1 path | 1+t |
| (5b) k-of-m inputs, 1 path | k(1+t) |
| (6) m inputs, in series | 1/2m(m+1) + m t |
| (7) m inputs, in parallel | m + m t |
| (8) tree | O(m logm + m t) |
| Table 2: Complexity of canonical scenarios |
The complexities for the above scenarios are summarized in
Table 2. Comparing the complexity of s in case (6)
to that in case (7), we see that dependencies that accumulate indirectly
result in a higher complexity
than dependencies that accumulate directly (in keeping with our
discussion comparing Fig. 1b and Fig. 1c).
A second observation, based on comparing cases (3) vs. (4a)
or (3) vs. (5a), is that our
metric neither penalizes nor rewards the use of redundant state.
This decision might seem to warrant discussion.
One might argue that redundancy should add to complexity
because of the additional effort that goes into creating redundant
state. For example, consider a server that must create m replicas
of an immutable file instead of just one.
While this is true, we note that (in this example) the replicas are
not dependent on each other and likewise state derived from
one of the replicas is ultimately only dependent on one rather than m
replicas and hence neither should have a complexity higher than if there
were only a single replica. That said, the additional effort due
to creating redundancy would emerge in the complexity of the
operation that creates the m copies since this requires maintaining
additional state to identify the m nodes at which to store replicas.
In terms of not rewarding redundancy, one might argue (as was
done in [34]) that a scenario in which s is derived from
k-of-m inputs should have lower complexity than if s were
derived from exactly k inputs because having alternate
options reduces the extent to which s depends on
any single input (and similarly for paths).
However, to do so would be conflating robustness and
complexity.1
in the sense that having alternate inputs does not ultimately change the
number of dependencies for s even though it changes the extent to
which s might depend on any individual input; i.e., the value of s derived
from k-of-m inputs does ultimately depend on some k input states.
5 Analysis
In this section we evaluate a number of networked system designs
through the lens of the complexity metric defined in
Section 4.
Our goal in this is to: (1) illustrate the application of our
metric to a broad range of systems and (2) provide concrete
examples of the assessments our metric arrives at both in comparing
across systems, and relative to traditional metrics.
To the extent possible, our hope is also to
validate that our metric matches common design intuition.
That said, conclusively validating the goodness of a metric is almost
by definition difficult and, in this sense, our results are perhaps better
viewed as providing the initial dataset for the future scrutiny of metric
performance.
We analyzed the complexity of solutions to four problems that figure
prominently in the literature on networked systems: (1) Internet routing,
(2) classical distributed systems, (3) resource discovery, and
(4) routing in wireless networks.
Due to space constraints we only discuss the first two items in this paper;
our complete set of results are presented in [9].
5.1 Routing
Routing is one of the fundamental tasks of a networked system and the
literature abounds in discussions of routing architectures and algorithms.
In this section we analyze a set of routing
solutions that
represent a range of design options in terms of architecture (e.g., centralized vs. distributed),
scalability (e.g., small vs. large tables), adoption and so forth.
For each solution, we present the complexity of an individual
routing entry and a source-to-destination routing operation.
For clarity we summarize only the final complexity results here and
present the details of their derivation in [9].
For comparison across metrics, we also evaluate each solution using
the following traditional measures: (1) per-node state, (2) number
of messages and (3) convergence time.2
In what follows, we consider each routing solution in turn, briefly
revise its operation and summarize its complexity.
The results of our analysis are summarized in
Tables 3 and 4 and we
end this section with a discussion examining these results.
| Algorithm | us | csV | csT
| cs | croute |
|
| DV | O(d) | O(d2) | O(dє) | O(d2+dє) | O(d3 + d2 є) |
| LS | O(d) | O(d) | O(d2є) | O(d+d2є) | O(d2 + d3 є) |
| RCP-inspired | O(d) | O(d) | O(d+d2 є) | O(d + d2 є) | O(d2 + d3 є) |
| RCP-inspired+SR | O(d) | O(d) | O(d+d2 є) | O(d + d2 є) | O(d + d2 є) |
| Compact | O(d√n) | O(n d2) | O(n d2) | O(n d2) | O(n d2) |
| Hierarchical LS | O(logn/k) | O(logn/k) | O(є log2 n/k) | O(logn/k + є log2 n/k) | O(log2 n/k + є log3 n/k) |
| Intradomain ROFL | O(d2) | O(d2 logn) | O(d3 є logn) | O((d2 + d3 є) logn) | O((d2 + d3 є) log2 n) |
| Table 3: Complexity analysis for routing solutions with the breakdown of the final per-state
complexity cs into its constituent components: us, the complexity contributed by value dependencies (csV) and the complexity contributed by transport dependencies (csT). |
| Algorithm | State | Message | Convergence time | Complexity |
|
| DV | O(n) | O(n2) | O(d) | O(d3 + d2 є) |
| LS | O(nf) | O(n3) | O(d) | O(d2 + d3 є) |
| RCP-inspired | O(n), center O(nf) | O(n3) | O(d) | O(d2 + d3 є) |
| RCP-inspired+SR | O(n), center O(nf) | O(n3) | O(d) | O(d + d2 є) |
| Compact | O(√n) | O(n√n) | O(d) | O(n d2) |
| Hierarchical LS | O(n/k + k) | O((n/k)3 + k3) | O(logn/k) | O(log2 n/k + є log3 n/k) |
| Intradomain ROFL | O(logn) | O(n log2 n) | O(d log2 n) | O((d2 + d3 є)log2 n) |
| Table 4: Evaluation of routing solutions using different metrics |
Distance-Vector (DV) Used by protocols such
as RIP and IGP, distance-vector represents one of the two major
classes of IP routing solutions.
DV protocols use the Bellman-Ford algorithm to calculate the
shortest path between pairs of nodes.
Every node maintains an estimate of its shortest distance (and
corresponding next-hop) to every
destination. Initially, a node is configured with
the distance to its immediate neighbors and assumes a distance of infinity for
all non-neighbor destinations.
Each node then periodically informs its neighbors of its currently estimated
distance to all destinations. For each destination, a node picks the
neighbor advertising the shortest path to the destination and updates its
estimated shortest distance and next-hop accordingly.
For an n node network with diameter d, DV thus requires O(n)
per-node state, a total
message cost of O(n2) and convergence time of O(d) in the
absence of topology changes.
In terms of our complexity measure, a single DV routing entry s has
complexity cs=O(d2 + dє)
while a routing operation has a
complexity of croute=O(d3 + d2є).3
Link-State (LS) Link-State routing, used in protocols
such as OSPF and IS-IS,
represents the second major class of widely-deployed IP routing solutions.
In LS, each node floods a “link state announcement (LSA)” describing
its immediate neighbor connections to the entire network. This allows
each node to reconstruct the complete network topology. To compute routes,
a node then simply runs Dijkstra’s algorithm over this topology map.
LS thus requires O(nf) state per node (where f denotes the average node
degree), incurs a total message cost of O(n3) and convergence time O(d).
A routing entry s has complexity cs=O(d+d2є)
while a routing operation has complexity
croute=O(d2 + d3 є).4
Centralized Architectures
The authors of the 4D project[15]
argue for architectures that centralize the routing control
plane to simplify network management.
Several subsequent proposals – RCP[5], SANE/Ethane[8, 7],
FCP[25] – present different instantiations of this centralized approach.
We analyze two variants of centralized routing solutions inspired by these proposals.
Our variants are not identical to any particular proposal but instead
adapt their key (routing) insights for a generic network context.
We do this because many of the above proposals were targeted at specific contexts
which complicates drawing comparisons across solutions if we were to
adopt them unchanged. For example, RCP assumes existing intra-domain
routing and leverages this to deliver forwarding state from the center to
the domain’s IGP routers.
In our first “RCP-inspired” variant, a designated center
node collects the LSAs flooded by all nodes, reconstructs the
complete network map from these LSAs, computes forwarding tables for all nodes
and then uses source routing to send each node its forwarding
table.5
When the network topology changes, the center receives
the new LSA, recomputes routes and updates the forwarding
state at relevant nodes.
RCP-inspired has a per-state complexity of cs=O(d+d2є) and
correspondingly, a routing operation complexity of croute=O(d2+d3є).
This can be intuitively inferred by noting that a routing
entry r computed at the center is similar to that at a node in LS;
r is then delivered to a node in the network using
a source route with the same complexity as r.
RCP’s performance with traditional metrics is summarized in Table 4.
RCP-inspired centralizes the computation of routes but packet
forwarding (i.e., the data plane) still relies on state distributed
across nodes along the path.
Borrowing from several recent routing proposals [8, 25],
our second variant “RCP-inspired + SR”
uses source routing to forward packets between
pairs of nodes. Routing construction proceeds as before but now the
forwarding table sent from the center to a node A contains the
entire route (as opposed to just the next hop) from A to each destination
and this information is used to source route packets originating at A.
Thus, rather than requiring O(d) routing entries (one at each node
along the path) for packet forwarding, our second variant requires only
the single source-route entry at the source thus retaining the
per-state complexity cs=O(d+d2є) but lowering the
complexity of croute to that of a single routing entry
and hence croute=O(d+d2є).
Compact routing
Compact routing [3, 10, 36, 2] has
significantly improved scalability (i.e., small
routing tables) relative to deployed solutions
but has seen little real-world adoption.
Here, we analyze the complexity of a state-of-the-art
name-independent6
routing algorithm by Abraham et al. (AG+_compact) [2].
AG+_compact guarantees optimally small routing tables of O(√n) entries,
worst-case stretch less than 3.0 for arbitrary topologies and ≈1.0
for Internet topologies[23] and hence – as per standard
measures – AG+_compact would appear to be an attractive
option for IP routing.
Briefly, AG+_compact operates as follows: a node A’s vicinity ball (denoted VB(A))
is defined as the k nodes closest to A. Node A maintains routing state
for every node in its own vicinity ball as well as for every node
B such that A ∈ VB(B).
A distributed coloring scheme assigns every node one of c colors.
One color, say red, serves as the global backbone
and every node in the network maintains routing state for all red nodes.
Finally, a node must know how to route to every other node of the
same color as itself.
For n nodes, vicinity balls of size k=Õ(√n)
and c=O(√n) colors, one can show that a node’s vicinity
ball contains every color.
With this construction, a node can always forward to a destination
that is either in its own vicinity, is red, or is of the same color
as the node itself. If none of these is true, the node forwards
the packet to a node in its vicinity that is the same color as
the destination.
The challenge in AG+_compact lies in setting up routes between nodes of the
same color without requiring state at intermediate nodes of a different
color and yet maintaining bounded stretch for all paths.
Loosely, AG+_compact achieves this as follows: say nodes A and D share the
same color and A is looking to construct a routing entry to D.
A explores every vicinity ball to which it belongs (VB(I), A ∈ VB(I))
and that touches or overlaps the vicinity ball of the destination
D (i.e., ∃ node X ∈ VB(I) with neighbor Y and Y ∈ VB(D)).
For such I, A could route to D via I, X and Y.
AG+_compact considers possible paths for each neighboring vicinity balls VB(I) as
well as the path through the red node closest to D and uses the shortest
of these for its routing entry to D.
AG+_compact incurs O(√n) per-node state, total message overhead of O(n√n)
and converges in O(d) rounds.
Derived in [9], AG+_compact has per-state complexity cs=O(nd2)
and croute=O(nd2).
Hierarchical routing
Compact routing represents one
effort to reduce routing table size.
The approach adopted by IP routing however has been to address
scalability through the use of hierarchy.
For example, OSPF may partition nodes into OSPF areas and
border routers of areas are connected into a backbone network.
Identifiers of nodes within a region are assigned
to be aggregatable (i.e., sharing a common prefix) so that
border routers need only advertise a single prefix to represent
all nodes within the region.
For a network partitioned into k areas, hierarchical routing
reduces the per-node state to O(n/k + k) and
total message overhead to O((n/k)3 + k3).
The resultant complexity depends on the network topology.
If the diameter of an area scales as logn/k,
then, from the LS complexity analysis, we know that
routing complexity in an area is
ca = log2 n/k + є log3 n/k.
The final routing complexity is 2 ca, which is
asymptotically equivalent to the complexity of non-hierarchical
routing O(log2 n + є log3 n).
Thus, in this case, hierarchy offers improved scalability
at no additional complexity. (If the network is planar,
hierarchy as above actually reduces complexity by O(√n)[9].)
Intradomain ROFL
Hierarchical routing offers improved scalability at the cost of constraining
address assignment (giving rise to several well-documented issues).
Intradomain ROFL [6] is a scalable routing protocol that
retains the ability to route on
flat (as opposed to aggregatable) identifiers.
Each virtual node maintains its predecessor and successor and
a pointer cache that stores source routes of virtual nodes
extracted from forwarded packets. In routing a packet, if a node
knows a virtual node whose identifier matches the label, it
sends the packet directly to the node; otherwise, it
forwards the packet to a node whose identifier is closest to the label
using a source route. Each node computes source routes
of its neighbors from a network topology map obtained from LSAs.
To simplify our analysis and comparison, we assume
that the pointer cache of a node contains fingers as in Chord [35]
to guarantee O(logn) hops in the flat label space and each node hosts
a single virtual node representing itself.
In intradomain ROFL, a node maintains routing entries, each of which
is (id, s, r) where id is a particular identifier, s is the successor of
id and r is a source route to the node hosting s.
Like in LS, cr = O(d2 + d3 є).
Finding s using a lookup operation takes O(logn) hops thus yielding
a complexity of cs = O(logn (d2 + d3 є)).
A routing operation involves logn such entries, hence results in
a complexity of croute = O(log2 n (d2 + d3 є)).
In other metrics, intradomain ROFL requires O(logn) state per node,
incurs a total message cost of O(n log2 n), and has
convergence time O(d log2 n).
5.1.1 Discussion
Tables 3 and 4
summarize our results which we now briefly examine.
In drawing comparisons,
we generally assume that the network diameter d is O(logn) and
є ∼ 0.
Complexity vs. traditional metrics
Our first observation is that none of the traditional metrics yield the same
relative ranking of solutions as our complexity metric, confirming that
complexity (as defined here) is not the same as scalability or efficiency.
Moreover, the ranking due to
our complexity metric is in fair agreement with that suggested by
real-world adoption and our survey results. For example, DV, LS and
hierarchical routing are simpler than either AG+_compact’s compact routing
algorithm or intradomain ROFL; centralized routing is simpler than DV,
compact routing or intradomain ROFL.
Our complexity measure is also more discriminating than the other
metrics. For example, DV, LS and both variants of centralized routing
fare equally in terms of total state or convergence time while
our metric ranks them as DV > LS = RCP-inspired > RCP-inspired + SR.
Convergence time in particular appears too coarse-grained – for
routing protocols it mostly reflects the scope to which state
propagates and hence most solutions have the same value.
In some sense, however, this greater discriminative power is to be
expected as our metric is somewhat more complicated in the sense of
taking more detail into account.
Deconstructing complexity
A routing entry at a node A for destination B depends fundamentally
on the link connectivity information from the d nodes along the path to B.
In DV, the computation mapping these d link states into a single routing
entry is distributed – occurring in stages at the multiple nodes
en route to A. LS by contrast, localizes this computation in
that the d pieces of state are transferred unchanged to node A which then
computes the route locally.
RCP not only localizes, but centralizes this computation.
Our metric ranks
distributed network computations as more complex than
localized ones and hence DV as more complex than LS.
Our metric ranks the complexity of LS as equal to that
of the first centralized variant implying that
a localized approach (i.e., “flood everywhere then compute locally”)
is similar in complexity to a centralized one (i.e., “flood to a central point, compute
locally, then flood from central point”).
This appears justified as
both approaches are ultimately similar in the number and manner in which
they accumulate dependencies.
While the central server can ensure an update is consistently
applied in computing routes for all nodes, it is still
left with the problem of consistently propagating those routes
to all nodes. LS must deal with the former issue but not
the latter and is thus merely making the inverse
tradeoff.
These “simpler” approaches that localize or centralize computations
might lead to greater message costs or reduced robustness and
this tradeoff could be made apparent by simultaneously considering
scalability, complexity and robustness metrics.
Introducing the use of source routing causes an O(d) reduction in the
complexity of the first RCP-inspired variant. Note too that
introducing source routing to LS would result in a similar reduction.
In some sense source routing localizes
decision making for the data plane in
much the same way as LS and RCP do for the control plane
and hence the reduced complexity points
again to the benefit of localized vs. distributed decision making.
Finally, we note that, assuming є → 0,
the combination of LS/RCP-inspired and source routing has O(d)
complexity which we conjecture might be optimal for directed routing
over an arbitrary topology.
In terms of navigating simplicity and scalability we note that –
unlike compact routing and intradomain ROFL –
introducing hierarchy improves scalability without increasing complexity.
From our analysis we find that the complexity of compact routing
is in large part because of the multiple passes needed to configure routing
tables – a node must first build its vicinity ball (VB), then hear from
nodes whose VBs it belongs to and finally explore the intersection
of “adjoining” VBs. We found a similar source of complexity in
our analysis of sensornet routing algorithms (presented in [9])
that use an initial configuration phase to elect landmark nodes
and then proceed to construct “virtual” coordinate systems based on distances
to these landmarks[33]. Such systems build up layers of
dependencies, leading to higher complexity.
Work on compact routing is typically cast as exploring the
tradeoff between efficiency (path stretch) and scalability (table size).
Throwing complexity into the ring enables discussing tradeoffs
between simplicity, efficiency and scalability.
For example, much of the complexity of AG+_compact stems from the additional
mechanisms needed to bound the worst-case stretch when routing between
nodes in adjoining vicinities (see [9]). Were we to
instead reuse the same mechanism for
nodes that are in adjoining vicinity balls as for those in distant
vicinities, this would
reduce the complexity of AG+_compact to O(√nd2)
but weaken the worst-case stretch bound.
In summary, we show that our complexity metric can discriminate across
a range of routing architectures, ranks solutions in a manner that
is congruent with common design intuition and can point
to alternate “simpler” design options and tradeoffs.
5.2 Classical Distributed Systems
In this section, we analyze the complexity of well-known
classical distributed system algorithms:
(1) shared read/write variables, (2) coordination/consensus,
(3) update propagation, and (4) cache consistency.
For each, we consider two solutions; one
that offers inferior performance/correctness guarantees
relative to the other but is typically viewed as being
simpler.
The algorithms we analyze operate under benign
fault assumptions and we assume transport states have complexity 1.
We denote by n the number of
servers and denote by k (> n/2) the quorum size.
The results are summarized in Table 5.
| Algorithm | State | Message | Complexity |
|
| ROWAA(read) | O(1) | O(1) | O(1) |
| ROWAA(write) | O(1) | O(n) | O(1) |
| Quorum(read) | O(1) | O(k) | O(k) |
| Quorum(write) | O(1) | O(k) | O(k2) |
|
| 2PC | O(1) | O(n) | O(n2) |
| Paxos | O(1) | O(n) | O(k3) |
|
| Multicast | O(n) | O(n) | O(log3 n) |
| Gossip | O(n) | O(n logn) | O(logn) |
|
| TTL-based | 1 | 1 | є |
| Invalidation | 1 | 1 | 2 |
| Table 5: Evaluation of classical distributed system algorithms using different metrics. |
5.2.1 Shared Read/Write Variable
For availability or performance, applications frequently replicate
the same data on multiple servers. The replicated data can be
viewed as a shared, replicated read/write variable
provided by a set of servers that allow multiple clients to read from,
and write to, the variable. We compare a best-effort read-one/write-all-available (in short, ROWAA) that favors availability over consistency
and quorum systems [28] used in cluster file systems such as
GPFS [1]. Our analysis assumes a client knows the set of servers
that participate in the algorithm.
ROWAA
In ROWAA, a client issues a read request to any one of the replicas, but
writes data to all available replicas in a best-effort manner.
A replica that is unavailable at the time of the write is not
updated and hence ROWAA can lead to inconsistency across replicas.
When a client reads a variable from a server, this fetched value (denoted by r) depends
only on the current value at that server. Therefore, crV=1.
Reading involves a request from the client to a server and the
response from the server; hence crT=2.
When a client writes a value to all available servers, it receives
any acknowledgments from the servers in a best-effort manner;
hence cw = O(1).
Quorum
Quorum systems allow clients to tolerate some number of server faults
while maintaining consistency although with lower read performance. To obtain
this property, the client reads from and writes to multiple replicas,
and the quorum protocol requires that there is at least one
correct replica that intersects a write quorum and a read quorum thereby
ensuring that the latest write is not missed by any client.
For this purpose, each value stored is tagged with a timestamp.
To read a variable in a quorum system, a client sends requests to k
servers and receives k (value, timestamp) pairs from a quorum. It
chooses the value with the highest timestamp. Since reading a value
depends on k (value, timestamp) pairs, cV = k. Since there
are k requests and k responses, cT=2k.
A write operation requires two phases. In the first phase, a client
sends a request to read the timestamp to each of the k servers.
When it receives timestamps from k servers, it chooses the
value with the highest
timestamp thigh and computes a new timestamp tnew greater
than thigh. tnew depends on k timestamps stored at
servers and these timestamps are fetched via k requests and k
responses. Therefore, c1V = k and c1T = 2k.
In the second phase, the client sends write
requests (value, tnew) to k servers and receives
acknowledgments from k servers. When a server receives this request,
it updates its local state s which depends on the value and tnew,
and hence csV = 2k+1 and csT = 2k + 1.
The client finishes the second phase
when it receives k acknowledgments from distinct servers.
Therefore, c2V = k(3k+3), c2T = k(2k+2)
and hence overall complexity c is O(k2).
Observations
Our complexity-based evaluation is in agreement with intuition
and our survey.
ROWAA has lower complexity but does not provide consistency; quorums
have higher complexity but ensure consistency.
This suggests that guaranteeing stronger properties (here, consistency)
may require more complex algorithms.
5.2.2 Coordination
Two-phase commit (in short, 2PC) [14] and
Paxos [26] coordinate a set of servers to implement a
consensus service. Both protocols operate in two phases and require
a coordinator that proposes a value and a set of acceptors, which are
servers that accept coordinated results. 2PC is commonly used in
distributed databases and Paxos is used for replicated state machines.
2PC requires that a coordinator communicate with
n servers; on the other hand, Paxos requires that a coordinator
(named as a proposer in Paxos) communicate with k servers, i.e., a
quorum of servers (named as acceptors in Paxos). Therefore, 2PC
cannot tolerate a single server fault, but Paxos can tolerate n−k
server faults.
2PC
In the first phase of 2PC, a coordinator multicasts to R (a set of acceptors)
a ⟨ prepare, T ⟩ message where T is a transaction.
When an acceptor receives the message, it makes a local decision on
whether to accept the transaction. If the decision is to accept T,
the acceptor sends a ⟨
ready, T ⟩ message to the coordinator. Otherwise, it sends a ⟨
no, T ⟩ message to the coordinator. The coordinator
collects responses from acceptors. Since the acceptor’s decision depends on
its local state and T sent by the coordinator,
the collection at the end of the first phase
has c1V = 3n. Since there
are n requests sent and n responses received,
the collection at the end of the first phase has
c1T = 2n.
In the second phase, if the coordinator receives ⟨ ready,
T ⟩ from all acceptors,
it multicasts to R a ⟨ commit, T ⟩ message. Otherwise,
it multicasts to R an ⟨ abort, T ⟩ message.
When an acceptor receives a request for commit or abort, it executes
the request and sends an ⟨ ack, T ⟩ back to the coordinator.
When the coordinator receives acknowledgments from all acceptors,
it knows that the transaction is completed.
Since the coordinator collects n acknowledgments,
c2V = n (7 n + 3) and c2T = n(2n+2)
at the completion of the second phase.
Hence 2PC has an overall complexity of O(n2).
Paxos
In Paxos, each acceptor maintains two important variables:
sm that denotes the highest proposal number the acceptor promised
to accept and va that denotes an accepted value.
A proposer multicasts to R a ⟨ prepare, s ⟩ message
where s is a proposal number. When an acceptor receives this message,
it compares s with sm.
If s > sm, the acceptor sets sm to s and
returns a ⟨ promise,
s, sa, va ⟩ message where sa is the proposal number for the
accepted value va. Otherwise, it returns an ⟨ error ⟩ message.
When the proposer receives ⟨ promise, s, sa, va ⟩ messages
from k distinct acceptors, it chooses va with the highest sa among
k messages. Let vc and sc be the chosen value and
proposal number, respectively. If va is not null,
vc is set to va; otherwise, vc is set to a default value.
The proposer then multicasts to R an ⟨ accept, sc, vc ⟩
message. When an acceptor receives the accept message, it compares sc
with its local sm. If sc ≥ sm, sm is set to sc,
sa is set to sc, and va is set to vc. It then
sends an ⟨ ack, sa, va ⟩ message to the coordinator.
Otherwise, it returns an ⟨ error ⟩ message.
When the proposer receives
⟨ ack, sa, va ⟩ messages from k distinct acceptors,
it knows that the message is accepted by k acceptors and completes
the consensus process.
Note that vc depends on va’s accepted by acceptors in the second phase.
To account for this dependency,
we use two passes to compute overall complexity. In the first pass,
we compute the dependency of va without considering the dependency in the
second phase. In the second pass, we use
the dependency of va computed in the first pass to compute the dependency
in the first phase and the total dependency of the algorithm.
In the first pass, cvcV = 3k
since vc depends on k sm’s and va’s, each of which
depends on s sent by the proposer. Also,
cvaV = 5k + 1
since va depends on vc and a default value.
cvaT = 2k + 1
since k prepare messages, k promise messages, and one accept message
are required.
In the second pass, cvcV = k(7k+5)
and the final cV = k(11k2 + 11k + 3), and
cvcT = k (2k + 3) and the final
cT = k (2k2 + 3k + 2).
Hence Paxos has an overall complexity of O(k3).
Observations
Our complexity-based evaluation is in agreement with general intuition
and our survey.
Both 2PC and Paxos use O(n) messages, maintain O(1) state per node,
and have the same operation time. However, Paxos is more complex than
2PC because of inter-dependencies between phases. At the same time,
it is this additional dependency that enables Paxos to tolerate
up to n−k faults while 2PC becomes unavailable with even a single fault.
Our results affirm once again that guaranteeing stronger properties
(here, fault-tolerance) may require more complex system algorithms.
5.2.3 Update Propagation
Update propagation algorithms disseminate an update from
a publisher to all nodes (e.g., publish-subscribe systems).
We examine multicast (e.g., ESM [20]) using a constructed tree
and Gossip [11] that exchanges updates with random nodes.
To ease comparison, we assume each node in the system
knows k random nodes in the system from a membership service.
Multicast
In multicast, nodes run DV over a k-degree mesh to build
a per-source tree over which messages are disseminated.
Hence forwarding state has complexity cs = O(log2 n
+ є logn).
A value received at a node depends only on the value published by
the source and hence cV = 1. On the other hand, if we assume
the tree is balanced, cT = O(cs logn)
and hence the overall complexity of multicast is O(log3 n).
Gossip
In Gossip, when a node receives a message, it chooses a random node and
forwards the message to the selected node. This process continues until
all nodes in the system receive the new update.
Hence cV = 1 as before.
Each transport depends on a single hop from a forwarding
node to a randomly chosen node, and in average logn such hops are required.
Hence cT = O(logn) and
the overall complexity of Gossip is O(logn).
Observations
Our metric ranks multicast as more complex than Gossip which
matches our survey. However, multicast offers a deterministic
guarantee of O(logn) delivery time and does so using
an optimal O(n) number of messages. Once again, our
results convey that efficiency need not be congruent with complexity.
5.2.4 Cache Consistency
When mutable data are replicated across multiple servers, a cache consistency
algorithm provides consistency across replicas.
We compare TTL-based caching to invalidation-based approaches.
TTL-based caching
In TTL-based caching, a cache server that receives a request first
checks whether the requested data item is locally available.
If so, it serves the client’s request directly. Otherwise, it fetches the item
from the corresponding origin server and stores the data item for its
associated time-to-live (TTL). After the TTL expires, the item is evicted from
the cache. Once a data item is cached, it does not depend on the item
value stored at the origin server and hence a cached data item has
c=є.
Invalidation
With approaches based on invalidation, the origin server tracks which
caches have copies of each data item. When a data item changes, the origin
server sends an invalidation to all caches storing that item. Since a cached
item depends on
the master copy of the origin server, cV = 1, cT = 1, and c = 2.
Observations
TTL-based caching is a soft-state technique while
invalidations are a hard-state technique.
Soft-state is typically viewed as simpler than hard-state
because of the lack of explicit state set-up and tear-down mechanisms
and our metric supports this valuation.
5.3 Other systems
Resource discovery is a fundamental problem in networked systems where
information is distributed across nodes in the network.
We subjected a number of well-known approaches to this problem
to our complexity based analysis. Due to space constraints,
because these solutions are well known in the community and
our results are (we hope) fairly intuitive, we only present
the final ranks of our analysis: centralized directory (e.g., Napster) <
(DNS, flooding-based (e.g., Gnutella)) < DHT.
The derivation of the complexities and discussion of the results
are described in [9].
We also analyzed several wireless routing solutions
including GPSR [21] (a scalable geo routing algorithm),
noGeo [33] (a scalable, but more complex solution that constructs “virtual”
geographic coordinates) and AODV [31] (a less scalable but widely
deployed approach).
At a high level, our results (described in [9]) reflect
a similar intuition as our analysis from Section 5.1 and
hence we do not discuss them here.
6 Discussion
Defining a metric involves walking the line between the
discriminating power of the metric (i.e., the level of detail in
system behavior that it can differentiate across) and
the simplicity of the metric itself.
Our prototype metric represents a particular point in that tradeoff.
We discuss some of the implications of this choice in this section.
6.1 Limitations and possible refinements
Weighting value vs. transport dependencies
Our metric assigns equal importance to
value and transport dependencies.
However, depending on the system environment, this may not be
the best choice and a more general form of the complexity equation might
be to assign:
| cs ← x = wv us← x + wt | | max(cy, є) + cx
|
For example, a system wherein the transport state is known
to be very stable while the data value of inputs change frequently
might choose wv ≫ wt, thus favoring system designs that
incur simpler value dependencies.
Weighting dependencies
Our metric treats all input
or transport states as equally important. However, sometime
certain input or transport states are more important (for
correctness, robustness, etc.) than others.
For example, DHTs maintain multiple routing entries but only
the immediate “successor” entry ensures
routing progress hence one might
emphasize the complexity due to successor.
Again, this might be achieved by weighting
states based on system-specific knowledge of their importance.
Correlated inputs Our metric treats all inputs
as independent which might result in over-counting
dependencies from correlated inputs.
This could be avoided by maintaining the set identifying
the actual dependencies associated with each piece of state
rather than just count their number although this
requires significantly more
fine-grained tracking of dependencies.
Capturing dependencies in time
In our counting-based approach we only consider the
inputs and transport states by which state was ultimately derived
without worrying about the precise temporal sequence of events that led to the
eventual value of state. While a time-based
analysis might enable a more fine-grained view of dependencies
this would also seem more complicated since it requires incorporating
a temporal model that captures the evolution of state over time.
Scalability vs. Complexity
As seen in the previous sections, our complexity metric complements
traditional scalability metrics.
As an example of their complementary nature: our metric would not penalize
system A that has the same per-state or per-operation complexity as
system B but constructs more state in total than B.
Correctness vs. Complexity
Our metric does little to validate the assumptions,
correctness or quality of a solution. For example, our metric might
capture the complexity of route construction but says little
about the quality or availability of the source-to-destination path.
Likewise, our metric is oblivious to undesirable assumptions
that might underlie a design.
For example, our metric ranks hierarchical routing favorably and
cannot capture the loss in flexibility due to its requirement of
aggregatable addresses (section 5.1).
Similarly, our metric ranks traditional geo routing as simple
despite its
problematic assumption of “uniform disc” connectivity[9].
Robustness vs. Complexity
Perhaps less obvious is the relationship between our complexity metric and robustness.
In some sense, our metric does relate to robustness since a more complex scaffolding of
dependencies does imply greater opportunities for failure.
However, this relation is indirect and does not always translate to robustness.
For example, consider a system where state at n nodes is derived from state
at a central server. Our complexity metric would assign
a low complexity to such a system, while, in terms of robustness,
such a system is vulnerable to the failure of the central server.
However, we conjecture that our dependency-centric viewpoint
might also apply to measuring robustness and this is something we
intend to explore in future work.
In particular, there are two aspects to dependencies that
appear important to robustness.
The first is the vulnerability of the system which could be
captured by counting the “reverse” dependencies of a state s as the
number of output states that derive from s.
The second aspect is the extent to which a piece of state is affected by
its various dependencies and this is a function of both the
importance of that dependency (e.g., the address of a server vs.
estimated latency to the server as a hint for better performance)
and the degree to which redundancy makes
the dependency less critical (i.e., deriving a piece of state from
any k of m inputs with k ≪ m is likely more robust that
one derived from k specific inputs). The former consideration
(importance) can be captured by weighting dependencies as proposed above.
A fairly straightforward extension to capture the effect of redundancy
would be to further weight complexity by
the fraction of states required; i.e., a weighted metric rs
of state s defined as: rs = r/m cs
where r and m are the required and available number of
inputs, respectively.
7 Related Work
There is much work – particularly in software engineering –
on measuring the complexity of a software program.
For example, Halstead’s
measures [18] capture programming effort
derived from a program’s source code.
Cyclomatic complexity [30],
simply put, measures the number of decision statements.
Fan in-fan out complexity [19] is a metric that measures
coupling between program components as the length of code times the square
of fan in times fan out. Kolmogorov complexity is measured as the
length of the program’s shortest description in a description
language (e.g., Turing machine).
These metrics work at the level of system implementation rather
than design, focus on a standalone program
and do not consider the distributed dependencies of
components that are networked. We believe the latter are key
to capturing complexity in networked systems and
both viewpoints are valuable.
Similarly, there is much work on improved approaches to
system specification with recent efforts that focus
on network contexts[22]. Metrics are
complementary to system specification and cleaner specifications
would make it easier to apply metrics for analysis.
An interesting question for future work is whether the
computation of network complexity (as we define it here) can
be derived from a system specification (or even code) in
an automated manner. This appears non-trivial as
the accumulation of distributed dependencies is
typically not obvious at the program or specification level.
While we derive our dependency-based metric from a system
design, there have been many recent efforts at inferring
dependencies or causality graphs from a running
system for use in network management, troubleshooting, and performance
debugging [16, 4, 12].
Finally, this paper builds on an earlier paper that articulated the
need for improved complexity metrics[34].
8 Conclusions
This paper takes a first step towards quantifying
the intuition for design simplicity that often guides
choices for practical systems.
We presented a metric that measures the impact of
the ensemble of distributed dependencies for an individual piece of state
and apply this metric to the evaluation of several
networked system designs.
While our metric is but a first step, we believe
the eventual ability to more rigorously quantify design
complexity would serve not only to improve our own design
methodologies but also to better articulate
our design aesthetic to the many communities that design for real-world
networked contexts (e.g., algorithms, formal distributed systems, graph theory).
Acknowledgments
We thank Matthew Caesar, Rodrigo Fonseca, Paul Francis,
Brighten Godfrey, Robert Kleinberg, Henry Lin, Scott Shenker, David Wetherall,
the anonymous reviewers and our shepherd, Ken Birman, for their comments.
References
-
[1]
-
IBM General Parallel File System (GPFS).
- [2]
-
I. Abraham, C. Gavoille, D. Malkhi, N. Nisan, and M. Thorup.
Compact name-independent routing with minimum stretch.
In Proc. of SPAA, 2004.
- [3]
-
B. Awerbuch, A. Bar-Noy, N. Linial, and D. Peleg.
Compact distributed data structures for adaptive routing.
In Proc. of STOC, 1989.
- [4]
-
P. Bahl, R. Chandra, A. Greenberg, S. Kandula, D. A. Maltz, and M. Zhang.
Towards highly reliable enterprise network services via inference of
multi-level dependencies.
In SIGCOMM, 2007.
- [5]
-
M. Caesar, D. Caldwell, N. Feamster, J. Rexford, A. Shaikh, and J. van der
Merwe.
Design and implementation of a routing control platform.
In Proc. of NSDI, 2005.
- [6]
-
M. Caesar, T. Condie, J. Kannan, K. Lakshminarayanan, I. Stoica, and
S. Shenker.
ROFL: Routing on flat labels.
In SIGCOMM, 2006.
- [7]
-
M. Casado, M. J. Freedman, J. Pettit, J. Luo, N. McKeown, and S. Shenker.
Ethane: Taking control of the enterprise.
In SIGCOMM, 2007.
- [8]
-
M. Casado, T. Garfinkel, A. Akella, M. J. Freedman, D. Boneh, N. McKeown, and
S. Shenker.
SANE: A protection architecture for enterprise networks.
In Proc. of USENIX Security, 2006.
- [9]
-
B.-G. Chun, S. Ratnasamy, and E. Kohler.
A complexity metric for networked system designs. IRB-TR-07-010.
- [10]
-
L. J. Cowen.
Compact routing with minimum stretch.
In Proc. of SODA, 1999.
- [11]
-
A. Demers, D. Greene, C. Hauser, W. Irish, J. Larson, S. Shenker, H. Sturgis,
D. Swinehart, and D. Terry.
Epidemic algorithms for replicated database maintenance.
In Proc. of PODC, 1987.
- [12]
-
R. Fonseca, G. Porter, R. Katz, S. Shenker, and I. Stoica.
X-trace: A pervasive network tracing framework.
In Proc. of NSDI, 2007.
- [13]
-
S. Gilbert and N. Lynch.
Brewer’s conjecture and the feasibility of consistent available
partition-tolerant web services.
SigACT News, 2002.
- [14]
-
J. Gray.
Notes on database systems.
IBM Research Report RJ2188, Feb. 1978.
- [15]
-
A. Greenberg, G. Hjalmtysson, D. A. Maltz, A. Myers, J. Rexford, G. Xie,
H. Yan, J. Zhan, and H. Zhang.
A clean slate 4d approach to network control and management.
In SIGCOMM CCR, 2005.
- [16]
-
B. Gruschke.
Integrated event management: Event correlation using dependency
graphs.
In Proc. of DSOM, 1998.
- [17]
-
K. P. Gummadi, H. V. Madhyastha, S. D. Gribble, H. M. Levy, and D. Wetherall.
Improving the reliability of Internet paths with one-hop source
routing.
In Proc. of OSDI, 2004.
- [18]
-
M. Halstead.
Elements of Software Science, Operating, and Programming
Systems.
Elsevier, 1977.
- [19]
-
S. Henry and D. Kafura.
Software structure metrics based on information flow.
IEEE Transactions on Software Engineering, pages 510–518,
1981.
- [20]
-
Y. hua Chu, S. G. Rao, and H. Zhang.
A case for end system multicast.
In Proc. of SIGMETRICS, 2000.
- [21]
-
B. Karp and H. T. Kung.
Greedy perimeter stateless routing for wireless networks.
In Proc. of MOBICOM, 2000.
- [22]
-
M. Karsten, S.Keshav, S. Prasad, and O. Beg.
An axiomatic basis for communication.
In SIGCOMM, 2007.
- [23]
-
D. Krioukov, K. Fall, and X. Yang.
Compact routing on Internet-like graphs.
In Proc. of INFOCOM, 2004.
- [24]
-
F. Kuhn and R. Wattenhofer.
On the complexity of distributed graph coloring.
In Proc. of PODC, 2006.
- [25]
-
K. Lakshminarayanan, M. Caesar, M. Rangan, T. Anderson, and S. Shenker.
Achieving convergence-free routing using failure-carrying packets.
In SIGCOMM, 2007.
- [26]
-
L. Lamport.
The part-time parliament.
ACM Trans. on Computer Systems, 16(2):133–169, May 1998.
- [27]
-
N. Linial.
Locality in distributed graph algorithms.
SIAM Journal on Computing, pages 193–201, 1992.
- [28]
-
D. Malkhi and M. Reiter.
Byzantine quorum systems.
In Proc. of STOC, 1997.
- [29]
-
Y. Mao, F. Wang, L. Qiu, S. S. Lam, and J. M. Smith.
S4: Small state and small stretch routing protocol for large wireless
sensor networks.
In Proc. of NSDI, 2007.
- [30]
-
T. J. McCabe and C. W. Butler.
Design complexity measurement and testing.
Comm. of the ACM, pages 1415–1425, 1989.
- [31]
-
C. E. Perkins and E. M. Royer.
Ad hoc on-demand distance vector routing.
In Proc. of WMCSA, 1999.
- [32]
-
R. Perlman, C.-Y. Lee, A. Ballardie, J. Crowcroft, Z. Wang, T. Maufer, C. Diot,
J. Thoo, and M. Green.
Simple multicast: A design for simple, low-overhead multicast.
Internet-Draft draft-perlman-simple-multicast-03, Internet
Engineering Task Force, Oct. 1999.
Work in progress.
- [33]
-
A. Rao, S. Ratnasamy, C. Papadimitriou, S. Shenker, and I. Stoica.
Geographic routing without location information.
In Proc. of MOBICOM, 2003.
- [34]
-
S. Ratnasamy.
Capturing complexity in networked systems design: The case for
improved metrics.
In Proc. of HotNets, 2006.
- [35]
-
I. Stoica, R. Morris, D. Karger, M. F. Kaashoek, and H. Balakrishnan.
Chord: A scalable peer-to-peer lookup service for Internet
applications.
In SIGCOMM, 2001.
- [36]
-
M. Thorup and U. Zwick.
Compact routing schemes.
In Proc. of SPAA, 2001.
Notes
1. We thank Paul Francis and Robert Kleinberg for
discussion on this.
2. We include this since the time complexity of distributed algorithms
is commonly used in the theory community [24, 27].
Time complexity is the maximum number of message-exchange rounds
needed to complete the required computation.
3. This can be inferred by noting that route
construction is similar to the canonical “m inputs in series” scenario from the previous section.
4. This is quickly inferred by noting the similarity to the “m inputs in parallel” scenario
with m=d inputs relayed along a path of O(d) hops and transport state of complexity є at each hop.
5. This use of source routing is the key difference
relative to RCP which uses the underlying intra-domain routes for the
same purpose.
6. We do not consider name-dependent algorithms [10, 29]
as these require an additional name translation service for IP routing.
This document was translated from LATEX by
HEVEA.