
Piyush Shivam![]() Varun Marupadi
Varun Marupadi![]() Jeff Chase
Jeff Chase![]() Thileepan Subramaniam
Thileepan Subramaniam![]() Shivnath Babu
Shivnath Babu![]()
![]() Sun Microsystems
Sun Microsystems
piyush.shivam@sun.com
![]() Duke University
Duke University
{varun,chase,thilee,shivnath}@cs.duke.edu
This paper explores a framework and policies to conduct such benchmarking activities automatically and efficiently. The workbench automation framework is designed to be independent of the underlying benchmark harness, including the server implementation, configuration tools, and workload generator. Rather, we take those mechanisms as given and focus on automation policies within the framework.
As a motivating example we focus on rating the peak load of an NFS file server for a given set of workload parameters, a common and costly activity in the storage server industry. Experimental results show how an automated workbench controller can plan and coordinate the benchmark runs to obtain a result with a target threshold of confidence and accuracy at lower cost than scripted approaches that are commonly practiced. In more complex benchmarking scenarios, the controller can consider various factors including accuracy vs. cost tradeoffs, availability of hardware resources, deadlines, and the results of previous experiments.
David Patterson famously said:
For better or worse, benchmarks shape a field.Systems researchers and developers devote a lot of time and resources to running benchmarks. In the lab, they give insight into the performance impacts and interactions of system design choices and workload characteristics. In the marketplace, benchmarks are used to evaluate competing products and candidate configurations for a target workload.
The accepted approach to benchmarking network server software and hardware is to configure a system and subject it to a stream of request messages under controlled conditions. The workload generator for the server benchmark offers a selected mix of requests over a test interval to obtain an aggregate measure of the server's response time for the selected workload. Server benchmarks can drive the server at varying load levels, e.g., characterized by request arrival rate for open-loop benchmarks [21]. Many load generators exist for various server protocols and applications.
Server benchmarking is a foundational tool for progress in systems research and development. However, server benchmarking can be costly: a large number of runs may be needed, perhaps with different server configurations or workload parameters. Care must be taken to ensure that the final result is statistically sound.
This paper investigates workbench automation techniques for server benchmarking. The objective is to devise a framework for an automated workbench controller that can implement various policies to coordinate experiments on a shared hardware pool or "workbench", e.g., a virtualized server cluster with programmatic interfaces to allocate and configure server resources [12,27]. The controller plans a set of experiments according to some policy, obtains suitable resources at a suitable time for each experiment, configures the test harness (system under test and workload generators) on those resources, launches the experiment, and uses the results and workbench status as input to plan or adjust the next experiments, as depicted in Figure 1. Our goal is to choreograph a set of experiments to obtain a statistically sound result for a high-level objective at low cost, which may involve using different statistical thresholds to balance cost and accuracy for different runs in the set.
As a motivating example, this paper focuses on the problem of measuring the peak throughput attainable by a given server configuration under a given workload (the saturation throughput or peak rate). Even this relatively simple objective requires a costly set of experiments that have not been studied in a systematic way. This task is common in industry, e.g., to obtain a qualifying rating for a server product configuration using a standard server benchmark from SPEC, TPC, or some other body as a basis for competitive comparisons of peak throughput ratings in the marketplace. One example of a standard server benchmark is the SPEC SFS benchmark and its predecessors [15], which have been used for many years to establish NFSOPS ratings for network file servers and filer appliances using the NFS protocol.
Systems research often involves more comprehensive benchmarking activities. For example, response surface mapping plots system performance over a large space of workloads and/or system configurations. Response surface methodology is a powerful tool to evaluate design and cost tradeoffs, explore the interactions of workloads and system choices, and identify interesting points such as optima, crossover points, break-even points, or the bounds of the effective operating range for particular design choices or configurations [17]. Figure 2 gives an example of response surface mapping using the peak rate. The example is discussed in Section 2. Measuring a peak rate is the "inner loop" for this response surface mapping task and others like it.
This paper illustrates the power of a workbench automation framework by exploring simple policies to optimize the "inner loop" to obtain peak rates in an efficient way. We use benchmarking of Linux-based NFS servers with a configurable workload generator as a running example. The policies balance cost, accuracy, and confidence for the result of each test load, while meeting target levels of confidence and accuracy to ensure statistically rigorous final results. We also show how advanced controllers can implement heuristics for efficient response surface mapping in a multi-dimensional space of workloads and configuration settings.
Figure 1 depicts a framework for automated server benchmarking. An automated workbench controller directs benchmarking experiments on a common hardware pool (workbench). The controller incorporates policies that decide which experiments to conduct and in what order, based on the following considerations:
 |
|
We characterize the benchmark performance of a server by its peak rate or
saturation throughput, denoted ![]() .
. ![]() is the highest
request arrival rate
is the highest
request arrival rate ![]() that does not drive the server into a saturation state. The server is said to be in a saturation state if a response
time metric exceeds a specified threshold, indicating that the offered load
has reached the maximum that the server
can process effectively.
that does not drive the server into a saturation state. The server is said to be in a saturation state if a response
time metric exceeds a specified threshold, indicating that the offered load
has reached the maximum that the server
can process effectively.
The performance of a server is a function of its workload, its configuration, and the hardware resources allocated to it. Each of these may be characterized by a vector of metrics or factors, as summarized in Table 1.
Workload ![]() . Workload factors define the properties of
the request mix and the data sets they operate on, and other workload
characteristics.
. Workload factors define the properties of
the request mix and the data sets they operate on, and other workload
characteristics.
Configurations (![]() ). The controller may vary server
configuration parameters (e.g., buffer sizes, queue bounds,
concurrency levels) before it instantiates the
server for each run.
). The controller may vary server
configuration parameters (e.g., buffer sizes, queue bounds,
concurrency levels) before it instantiates the
server for each run.
Resources ![]() . The controller can vary the amount of hardware
resources assigned to the system under test, depending on the capabilities
of the workbench testbed. The prototype can instantiate Xen virtual machines
sized along the memory, CPU, and I/O dimensions.
The experiments in this paper vary the workload and configuration
parameters on a fixed set of
Linux server configurations in the workbench.
. The controller can vary the amount of hardware
resources assigned to the system under test, depending on the capabilities
of the workbench testbed. The prototype can instantiate Xen virtual machines
sized along the memory, CPU, and I/O dimensions.
The experiments in this paper vary the workload and configuration
parameters on a fixed set of
Linux server configurations in the workbench.
This paper uses NFS server benchmarking as a running example.
The controllers use a
configurable synthetic NFS workload
generator called Fstress [1],
which was developed in previous research.
Fstress offers knobs for various
workload factors (![]() ), enabling
the controller to configure the
properties of the workload's dataset
and its request mix to explore a space of NFS workloads.
Fstress has
preconfigured parameter sets that represent
standard NFS file
server workloads (e.g., SPECsfs97, Postmark),
as well as many other workloads that might be
encountered in practice (see Table 3).
), enabling
the controller to configure the
properties of the workload's dataset
and its request mix to explore a space of NFS workloads.
Fstress has
preconfigured parameter sets that represent
standard NFS file
server workloads (e.g., SPECsfs97, Postmark),
as well as many other workloads that might be
encountered in practice (see Table 3).
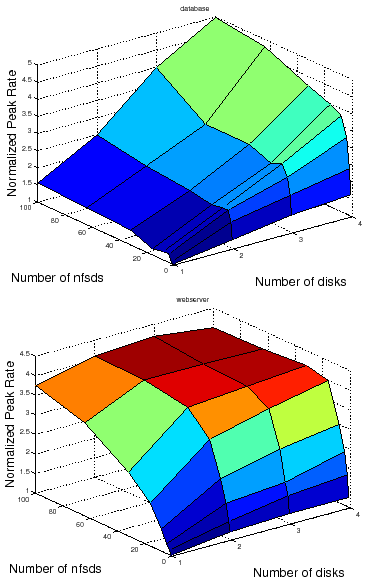
Figure 2 shows an example of response surfaces produced by the automated workbench for two canned NFS server workloads representing typical request mixes for a file server that backs a database server (called DB_TP) and a static Web server (Web server). A response surface gives the response of a metric (peak rate) to changes in the operating range of combinations of factors in a system [17]. In this illustrative example the factors are the number of NFS server daemons (nfsds) and disk spindle counts.
Response surface mapping can yield insights into the performance effects of configuration choices in various settings. For example, Figure 2 confirms the intuition that adding more disks to an NFS server can improve the peak rate only if there is a sufficient number of nfsds to issue requests to those disks. More importantly, it also reveals that the ideal number of nfsds is workload-dependent: standard rules of thumb used in the field are not suitable for all workloads.
The challenge for the automated feedback-driven workbench controller is to design a set of experiments to obtain accurate peak rates for a set of test points, and in particular for test points selected to approximate a response surface efficiently.
Response surface mapping is expensive.
Algorithm 1 presents the overall benchmarking approach that is
used by the workbench controller to map a response surface, and
Table 2 summarizes some relevant notation.
The overall approach
consists of an outer loop that iterates over selected samples from
![]() , where
, where
![]() is a subset of factors in the
larger
is a subset of factors in the
larger
![]() space (Step 2). The inner loop
(Step 3) finds the peak rate
space (Step 2). The inner loop
(Step 3) finds the peak rate ![]() for each sample by generating a series
of test loads for the sample. For each test load
for each sample by generating a series
of test loads for the sample. For each test load ![]() , the controller must choose
the runlength
, the controller must choose
the runlength ![]() or observation interval, and the
number of independent trials
or observation interval, and the
number of independent trials
![]() to obtain a response time measure under load
to obtain a response time measure under load ![]() .
.
The goal of the automated feedback-driven controller is to address the following problems.
Minimizing benchmarking cost involves choosing values carefully for the
runlength ![]() , the number of trials
, the number of trials ![]() , and test loads
, and test loads ![]() so that the
controller converges quickly to the peak rate.
Sections 3 and 4
present algorithms that the controller uses to address these problems.
so that the
controller converges quickly to the peak rate.
Sections 3 and 4
present algorithms that the controller uses to address these problems.
Benchmarking can never produce an exact result because
complex systems exhibit inherent variability in their behavior.
The best we can do is to make a probabilistic claim about the
interval in which the "true" value for a metric lies based on
measurements from multiple independent trials [13].
Such a claim can be characterized by a confidence level and the
confidence interval at this confidence level.
For example, by
observing the mean response time ![]() at a test load
at a test load ![]() for
for ![]() independent
trials, we may be able to claim that we are
independent
trials, we may be able to claim that we are ![]() % confident (the confidence
level) that the correct value of
% confident (the confidence
level) that the correct value of ![]() for that
for that ![]() lies within the range
lies within the range
![]() (the confidence interval).
(the confidence interval).
Basic statistics tells us how to compute confidence intervals and levels from a
set of trials. For example, if the mean server response time ![]() from
from ![]() trials is
trials is
![]() , and standard deviation is
, and standard deviation is ![]() , then the confidence interval for
, then the confidence interval for
![]() at confidence level
at confidence level ![]() is given by:
is given by:
![]() is a reading from the table of standard normal distribution for
confidence level
is a reading from the table of standard normal distribution for
confidence level ![]() . If
. If ![]() , then we use Student's t distribution
instead after verifying that the
, then we use Student's t distribution
instead after verifying that the ![]() runs come from a normal
distribution [13].
runs come from a normal
distribution [13].
The tightness of the confidence interval captures the accuracy of the
true value of the metric.
A tighter bound implies that the mean response time
from a set of trials is closer to its true value.
For a confidence
interval
![]() , we compute the percentage accuracy as:
, we compute the percentage accuracy as:
|
In the inner loop of Algorithm 1, the automated controller
searches for the peak rate ![]() for some workload and
configuration given by a selected sample of factor values in
for some workload and
configuration given by a selected sample of factor values in
![]() . To find the peak rate it subjects the server to a sequence of test loads
. To find the peak rate it subjects the server to a sequence of test loads
![]() . The sequence of test loads should
converge on an estimate
of the peak rate
. The sequence of test loads should
converge on an estimate
of the peak rate ![]() that meets the target accuracy and confidence.
that meets the target accuracy and confidence.
We emphasize that this step is itself a common benchmarking task to determine a standard rating for a server configuration in industry (e.g., SPECsfs [6]).
Common practice for finding the peak rate is to script a sequence of runs for a
standard workload at a fixed linear sequence of escalating
load levels, with a preconfigured runlength ![]() and number of trials
and number of trials ![]() for
each load level. The algorithm is in essence a linear search for the peak
rate: it starts at a
default load level and increments the load level (e.g., arrival rate) by some
fixed increment until it drives the server
into saturation. The last load level
for
each load level. The algorithm is in essence a linear search for the peak
rate: it starts at a
default load level and increments the load level (e.g., arrival rate) by some
fixed increment until it drives the server
into saturation. The last load level ![]() before saturation is taken as
the peak rate
before saturation is taken as
the peak rate ![]() . We refer to this algorithm as strawman.
. We refer to this algorithm as strawman.
 |
 |
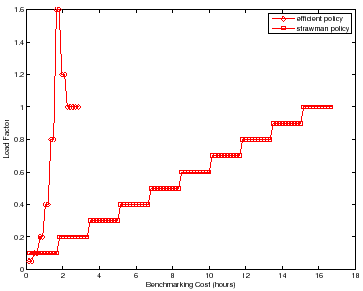
Strawman is not efficient. If the increment is too small, then it requires many iterations to reach the peak rate. Its cost is also sensitive to the difference between the peak rate and the initial load level: more powerful server configurations take longer to benchmark. A larger increment can converge on the peak rate faster, but then the test may overshoot the peak rate and compromise accuracy. In addition, strawman misses opportunities to reduce cost by taking "rough" readings at low cost early in the search, and to incur only as much cost as necessary to obtain a statistically sound reading once the peak rate is found.
A simple workbench controller with feedback can improve significantly on the
strawman approach to searching for the peak rate. To illustrate,
Figure 3 depicts the search for ![]() for two
policies conducting a sequence of experiments, with no concurrent testing. For
strawman we use runlength
for two
policies conducting a sequence of experiments, with no concurrent testing. For
strawman we use runlength ![]() =
= ![]() minutes,
minutes, ![]() trials, and a small
increment to produce an accurate result. The figure compares strawman to
an alternative that converges quickly on the peak rate using binary search, and
that adapts
trials, and a small
increment to produce an accurate result. The figure compares strawman to
an alternative that converges quickly on the peak rate using binary search, and
that adapts ![]() and
and ![]() dynamically to balance accuracy, confidence, and cost
during the search. The figure represents the sequence of actions taken by each
policy with cumulative benchmarking time on the x-axis; the y-axis gives the
load factor
dynamically to balance accuracy, confidence, and cost
during the search. The figure represents the sequence of actions taken by each
policy with cumulative benchmarking time on the x-axis; the y-axis gives the
load factor
![]() for each test load evaluated by
the policies. The figure shows that strawman can incur a much higher
benchmarking cost (time) to converge to the peak rate and complete the search
with a final accurate reading at load factor
for each test load evaluated by
the policies. The figure shows that strawman can incur a much higher
benchmarking cost (time) to converge to the peak rate and complete the search
with a final accurate reading at load factor ![]() . The strawman policy not
only evaluates a large number of test loads with load factors that are not close
to
. The strawman policy not
only evaluates a large number of test loads with load factors that are not close
to ![]() , but also incurs unnecessary cost at each load.
, but also incurs unnecessary cost at each load.
The remainder of the paper discusses the improved controller policies in more detail, and their interactions with the outer loop in mapping response surfaces.
The runlength ![]() and the number of trials
and the number of trials ![]() together determine the
benchmarking cost incurred at a given test load
together determine the
benchmarking cost incurred at a given test load ![]() . The controller
should choose
. The controller
should choose ![]() and
and ![]() to obtain the confidence and accuracy desired for each
test load at least cost. The goal is to converge quickly to an accurate reading
at the peak rate:
to obtain the confidence and accuracy desired for each
test load at least cost. The goal is to converge quickly to an accurate reading
at the peak rate:
![]() and load factor
and load factor ![]() . High
confidence and accuracy are needed for the final test load at
. High
confidence and accuracy are needed for the final test load at
![]() , but accuracy is less crucial during the search for the peak rate.
Thus the controller has an opportunity to reduce benchmarking cost by adapting
the target confidence and accuracy for each test load
, but accuracy is less crucial during the search for the peak rate.
Thus the controller has an opportunity to reduce benchmarking cost by adapting
the target confidence and accuracy for each test load ![]() as the search
progresses, and choosing
as the search
progresses, and choosing ![]() and
and ![]() for each
for each ![]() appropriately.
appropriately.
At any given load level the controller can trade off confidence and
accuracy for lower cost by decreasing either ![]() or
or ![]() or both.
Also, at a given cost
any given set of trials and runlengths can give a high-confidence
result with wide confidence intervals (low accuracy), or a narrower confidence
interval (higher accuracy) with lower confidence.
or both.
Also, at a given cost
any given set of trials and runlengths can give a high-confidence
result with wide confidence intervals (low accuracy), or a narrower confidence
interval (higher accuracy) with lower confidence.
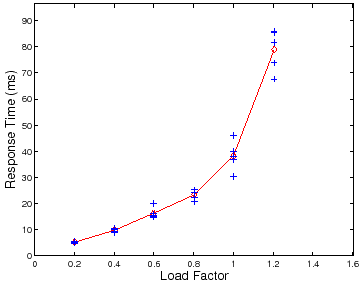
However, there is a complication: performance variability tends to increase as
the load factor ![]() approaches saturation. Figure 4 and
Figure 5 illustrate this effect. Figure 4 is a
scatter plot of mean server response time (
approaches saturation. Figure 4 and
Figure 5 illustrate this effect. Figure 4 is a
scatter plot of mean server response time (![]() ) at different test loads
) at different test loads
![]() for five trials at each load. Note that the variability across
multiple trials increases as
for five trials at each load. Note that the variability across
multiple trials increases as
![]() and
and
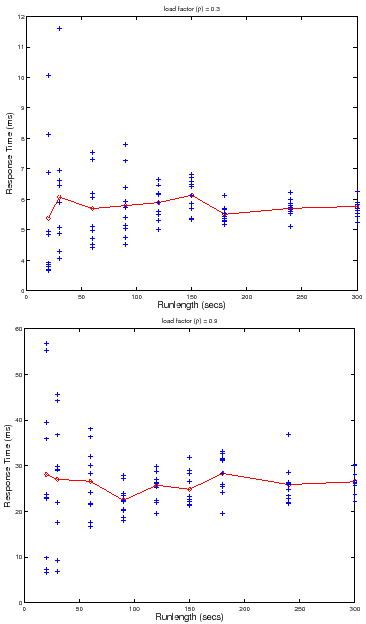
![]() . Figure 5 shows a scatter plot of
. Figure 5 shows a scatter plot of ![]() measures for multiple runlengths at two load factors,
measures for multiple runlengths at two load factors,
![]() and
and
![]() . Longer runlengths show less variability at any load factor, but for a
given runlength, the variability is higher at the higher load factor. Thus the
cost for any level of confidence and/or accuracy also depends on load level:
since variability increases at higher load factors, it requires longer
runlengths
. Longer runlengths show less variability at any load factor, but for a
given runlength, the variability is higher at the higher load factor. Thus the
cost for any level of confidence and/or accuracy also depends on load level:
since variability increases at higher load factors, it requires longer
runlengths ![]() and/or a larger number of trials
and/or a larger number of trials ![]() to reach a target level of
confidence and accuracy.
to reach a target level of
confidence and accuracy.
For example, consider the set of trials plotted in Figure 5. At
load factor ![]() and runlength of
and runlength of ![]() seconds, the data gives us
seconds, the data gives us ![]() %
confidence that
%
confidence that
![]() , or
, or ![]() % confidence that
% confidence that
![]() . From the data we can determine the runlength needed to achieve target
confidence and accuracy at this load level and number of trials
. From the data we can determine the runlength needed to achieve target
confidence and accuracy at this load level and number of trials ![]() : a runlength
of
: a runlength
of ![]() seconds achieves an accuracy of
seconds achieves an accuracy of ![]() % with
% with ![]() % confidence, but it
takes a runlength of
% confidence, but it
takes a runlength of ![]() seconds to achieve
seconds to achieve ![]() % accuracy with
% accuracy with ![]() %
confidence. Accuracy and confidence decrease with higher load factors. For
example, at load factor
%
confidence. Accuracy and confidence decrease with higher load factors. For
example, at load factor ![]() and runlength
and runlength ![]() , the data gives us
, the data gives us ![]() %
confidence that
%
confidence that
![]() (
(![]() % accuracy), or
% accuracy), or ![]() % confidence
that
% confidence
that
![]() (
(![]() % accuracy). As a result, we must increase the
runlength and/or the number of trials to maintain target levels of confidence
and accuracy as load factors increase. For example, we need a runlength of
% accuracy). As a result, we must increase the
runlength and/or the number of trials to maintain target levels of confidence
and accuracy as load factors increase. For example, we need a runlength of
![]() seconds or more to achieve accuracy
seconds or more to achieve accuracy ![]() % at
% at ![]() % confidence for
this number of trials at load factor
% confidence for
this number of trials at load factor ![]() .
.
Figure 6 quantifies the tradeoff between the
runlength and the number of trials required to attain a target accuracy and
confidence for different workloads and load factors. It shows the number of
trials required to meet an accuracy of ![]() % at
% at ![]() % confidence level for
different runlengths. The figure shows that to attain a target accuracy and
confidence, one needs to conduct more independent trials at shorter runlengths.
It also shows a sweet spot for the runlengths that reduces the number of trials
needed. A controller can use such curves as a guide to pick a suitable
runlength
% confidence level for
different runlengths. The figure shows that to attain a target accuracy and
confidence, one needs to conduct more independent trials at shorter runlengths.
It also shows a sweet spot for the runlengths that reduces the number of trials
needed. A controller can use such curves as a guide to pick a suitable
runlength ![]() and number of trials
and number of trials ![]() with low cost.
with low cost.
 |
 |
![\begin{algorithm}
% latex2html id marker 944
[t]
\caption{Searching for the Peak...
...e{3ex} {\bf end}
\par
}
{\bf end}
}
\par
\end{list}\vspace{-3ex}
\end{algorithm}](img75.png)
Our approach uses Algorithm 2 to search for the peak rate for a given setting of factors.
Algorithm 2 takes various parameters to define the conditions for the reported peak rate:
Algorithm 2 chooses
(a) a sequence of test loads to try; (b) the number of independent trials at any test load;
and (c) the runlength of the workload at that load.
It automatically adapts the number of trials at any
test load according to the load factor and the desired target confidence and
accuracy.
At each load level the algorithm conducts
a small (often the minimum of two in our experiments) number of trials
to establish with ![]() % confidence that the current
test load is not the peak rate (Step
% confidence that the current
test load is not the peak rate (Step ![]() ). However, as soon as the algorithm
identifies a test load
). However, as soon as the algorithm
identifies a test load ![]() to be a potential peak rate, which happens near a load
factor of
to be a potential peak rate, which happens near a load
factor of ![]() , it spends just enough time to check whether it is in fact
the peak rate.
, it spends just enough time to check whether it is in fact
the peak rate.
More specifically,
for each test load
![]() , Algorithm 2
first conducts two
trials to generate an initial confidence interval for
, Algorithm 2
first conducts two
trials to generate an initial confidence interval for
![]() ,
the mean server response time at load
,
the mean server response time at load
![]() , at
, at ![]() % confidence
level. (Steps
% confidence
level. (Steps ![]() and
and ![]() in Algorithm 2.) Next, it checks if
the confidence interval overlaps with the specified peak-rate region (Step
in Algorithm 2.) Next, it checks if
the confidence interval overlaps with the specified peak-rate region (Step
![]() ).
).
If the regions overlap, then Algorithm 2
identifies the current test load
![]() as an estimate of a potential
peak rate with 95% confidence.
It then computes the accuracy of the mean server response time
as an estimate of a potential
peak rate with 95% confidence.
It then computes the accuracy of the mean server response time
![]() at the current test load, at the target confidence
level
at the current test load, at the target confidence
level ![]() (Section 2.1). If it reaches
the target accuracy
(Section 2.1). If it reaches
the target accuracy ![]() , then the algorithm terminates (Step
, then the algorithm terminates (Step
![]() ), otherwise it conducts more trials at the current test load (Step
), otherwise it conducts more trials at the current test load (Step ![]() )
to narrow the confidence interval, and repeats the threshold condition test.
Thus the cost of the algorithm varies with
the target confidence and accuracy.
)
to narrow the confidence interval, and repeats the threshold condition test.
Thus the cost of the algorithm varies with
the target confidence and accuracy.
If there is no overlap (Step ![]() ), then
Algorithm 2 moves on to the next test load.
It uses any of several load-picking algorithms
to generate the sequence of test loads, described in the rest of this section.
All load-picking algorithms take as input the set of past test loads
and their results. The output becomes the next test load in
Algorithm 2. For example,
Algorithm 3 gives a load-picking algorithm using
a simple binary search.
), then
Algorithm 2 moves on to the next test load.
It uses any of several load-picking algorithms
to generate the sequence of test loads, described in the rest of this section.
All load-picking algorithms take as input the set of past test loads
and their results. The output becomes the next test load in
Algorithm 2. For example,
Algorithm 3 gives a load-picking algorithm using
a simple binary search.
To simplify the choice of runlength for each experiment at a test load (Step 5),
Algorithm 2 uses the "sweet spot" derived from
Figure 6 (Section 3.2). The figure
shows that for all workloads that this paper considers, a runlength of ![]() minutes is the sweet spot for the minimum number of trials.
minutes is the sweet spot for the minimum number of trials.
Algorithm 3 outlines the Binsearch algorithm. Intuitively, Binsearch keeps doubling the current test load until it finds a load that saturates the server. After that, Binsearch applies regular binary search, i.e., it recursively halves the most recent interval of test loads where the algorithm estimates the peak rate to lie.
Binsearch allows the controller to find the lower and upper bounds for the peak rate within a logarithmic number of test loads. The controller can then estimate the peak rate using another logarithmic number of test loads. Hence the total number of test loads is always logarithmic irrespective of the start test load or the peak rate.
The Linear algorithm is similar to Binsearch except in the initial phase of finding the lower and upper bounds for the peak rate. In the initial phase it picks an increasing sequence of test loads such that each load differs from the previous one by a small fixed increment.
The general shape of the response-time vs. load curve is well known, and
the form is similar for different workloads and server configurations.
This suggests that a model-guided approach could fit the curve from a few
test loads and converge more quickly to the peak rate.
Using the insight offered by well-known
open-loop queuing theory results [13],
we experimented with a simple model to fit the curve:
![]() , where
, where ![]() is the
response time,
is the
response time, ![]() is the load, and
is the load, and ![]() and
and ![]() are constants that depend
on the settings of factors in
are constants that depend
on the settings of factors in
![]() . To
learn the model, the controller needs tuples of the form
. To
learn the model, the controller needs tuples of the form
![]() .
.
Algorithm 4 outlines the model-guided algorithm. If there
are insufficient tuples for learning the model, it uses a simple
heuristic to pick the test loads for generating the tuples. After that, the
algorithm uses the model to predict the peak rate
![]() for
for
![]() , returns the prediction as the next test load, and relearns the model
using the new
, returns the prediction as the next test load, and relearns the model
using the new
![]() tuple at the prediction.
The whole process repeats until the search converges to the peak rate. As the
controller observes more
tuple at the prediction.
The whole process repeats until the search converges to the peak rate. As the
controller observes more
![]() tuples, the
model-fit should improve progressively, and the model should guide the search
to an accurate peak rate. In many cases, this happens in a single iteration of
model learning (Section 5).
tuples, the
model-fit should improve progressively, and the model should guide the search
to an accurate peak rate. In many cases, this happens in a single iteration of
model learning (Section 5).
However, unlike the previous approaches, a model-guided search is not guaranteed
to converge. Model-guided search is dependent on the accuracy of the model,
which in turn depends on the choice of
![]() tuples that are used for learning. The choice of tuples is generated by previous
model predictions. This creates the possibility of learning an
incorrect model which in turn yields incorrect choices for test loads.
For example, if most of the test loads chosen for learning the model happen to
lie significantly outside the peak rate region, then the model-guided choice of
test loads may be incorrect or inefficient. Hence, in the worst case, the
search may never converge or converge slowly to the peak rate. We have
experimented with other models including polynomial models of the form
tuples that are used for learning. The choice of tuples is generated by previous
model predictions. This creates the possibility of learning an
incorrect model which in turn yields incorrect choices for test loads.
For example, if most of the test loads chosen for learning the model happen to
lie significantly outside the peak rate region, then the model-guided choice of
test loads may be incorrect or inefficient. Hence, in the worst case, the
search may never converge or converge slowly to the peak rate. We have
experimented with other models including polynomial models of the form
![]() , which show similar limitations.
, which show similar limitations.
To avoid the worst case, the algorithm uses a simple heuristic to choose the
tuples from the list of available tuples. Each time the controller learns the
model, it chooses two tuples such that one of them is the last prediction, and
the other is the tuple that yields the response time closest to threshold mean
server response time ![]() . More robust techniques for choosing the tuples
is a topic of ongoing study. Section 5 reports our experience with
the model-guided choice of test loads. Preliminary results
suggest that the
model-guided approaches are often superior but
can be unstable depending on the initial samples used to learn the model.
. More robust techniques for choosing the tuples
is a topic of ongoing study. Section 5 reports our experience with
the model-guided choice of test loads. Preliminary results
suggest that the
model-guided approaches are often superior but
can be unstable depending on the initial samples used to learn the model.
The load-picking algorithms in Sections 3.5-3.6 generate a new load given one or more previous test loads. How can the controller generate the first load, or seed, to try? One way is to use a conservative low load as the seed, but this approach increases the time spent ramping up to a high peak rate. When the benchmarking goal is to plot a response surface, the controller uses another approach that uses the peak rate of the "nearest" previous sample as the seed.
To illustrate, assume that the factors of interest,
![]() , in Algorithm 1 are
, in Algorithm 1 are ![]() number of disks, number
of nfsds
number of disks, number
of nfsds ![]() (as shown in Figure 2). Suppose the
controller uses Binsearch with a low seed of
(as shown in Figure 2). Suppose the
controller uses Binsearch with a low seed of ![]() to find the peak rate
to find the peak rate
![]() for sample
for sample
![]() . Now, for finding the peak
rate
. Now, for finding the peak
rate
![]() for sample
for sample
![]() , it can use the peak
rate
, it can use the peak
rate
![]() as seed. Thus, the controller can jump quickly to a load
value close to
as seed. Thus, the controller can jump quickly to a load
value close to
![]() .
.
In the common case, the peak rates for "nearby" samples will be close. If they are not, the load-picking algorithms may incur additional cost to recover from a bad seed. The notion of "nearnest" is not always well defined. While the distance between samples can be measured if the factors are all quantitative, if there are categorical factors--e.g., file system type--the nearest sample may not be well defined. In such cases the controller may use a default seed or an aggregate of peak rates from previous samples to start the search.
We now relate the peak rate algorithm that Section 3 describes to the larger challenge of mapping a peak rate response surface efficiently and effectively, based on Algorithm 1.
A large number of factors can affect performance,
so it is important to
sample the multi-dimensional space with care as well as to optimize
the inner loop. For
example, suppose we are mapping the impact of five factors on a file server's
peak rate, and that we sample five values for each factor. If the benchmarking
process takes an hour to find the peak rate for each factor combination, then
the total time for benchmarking is ![]() days. An automated workbench
controller can shorten this time by pruning the sample space, planning
experiments to run on multiple hardware setups in parallel, and optimizing the
inner loop.
days. An automated workbench
controller can shorten this time by pruning the sample space, planning
experiments to run on multiple hardware setups in parallel, and optimizing the
inner loop.
We consider two specific challenges for mapping a response surface:
If the benchmarking objective is to understand the overall trend of
how the peak rate is affected by certain factors of interest
![]() --rather than finding accurate peak rate
values for each sample in
--rather than finding accurate peak rate
values for each sample in
![]() --then
Algorithm 1 can leverage
Response Surface Methodology
(RSM) [17] to
select the sample points efficiently (in Step 2).
RSM is a branch of statistics that provides principled techniques to choose a
set of samples to obtain good approximations of the
overall response surface at low cost.
For example, some RSM techniques
assume that a low-degree multivariate polynomial model-- e.g., a quadratic
equation of the form
--then
Algorithm 1 can leverage
Response Surface Methodology
(RSM) [17] to
select the sample points efficiently (in Step 2).
RSM is a branch of statistics that provides principled techniques to choose a
set of samples to obtain good approximations of the
overall response surface at low cost.
For example, some RSM techniques
assume that a low-degree multivariate polynomial model-- e.g., a quadratic
equation of the form
![]() -- approximates the surface in the
-- approximates the surface in the ![]() -dimensional
-dimensional
![]() space. This approximation is a basis
for selecting a minimal
set of samples for the controller to obtain in order to learn a
fairly accurate model (i.e., estimate values of the
space. This approximation is a basis
for selecting a minimal
set of samples for the controller to obtain in order to learn a
fairly accurate model (i.e., estimate values of the ![]() parameters in the
model). We evaluate one such RSM technique in Section 5.
parameters in the
model). We evaluate one such RSM technique in Section 5.
It is important to note that these RSM techniques may reduce the effectiveness of the seeding heuristics described in Section 3.7. RSM techniques try to find sample points on the surface that will add the most information to the model. Intuitively, such samples are the ones that we have the least prior information about, and hence for which seeding from prior results would be least effective. We leave it to future work to explore the interactions of the heuristics for selecting samples efficiently and seeding the peak rate search for each sample.
Cost for Finding Peak Rate. Sections 3.3 and 4 present several policies for finding the peak rate. We evaluate those policies as follows:
Cost for Mapping Response Surfaces. We compare the total benchmarking cost for mapping the response surface across all the samples.
Cost Versus Target Confidence and Accuracy. We demonstrate that the policies adapt the total benchmarking cost to target confidence and accuracy. Higher confidence and accuracy incurs higher benchmarking cost and vice-versa.
Section 5.1 presents the experiment setup. Section 5.2 presents the workloads that we use for evaluation. Section 5.3 evaluates our benchmarking methodology as described above.
Table 1 shows the factors in the
![]() vectors for a storage server. We benchmark an NFS server to evaluate
our methodology. In our evaluation, the factors in
vectors for a storage server. We benchmark an NFS server to evaluate
our methodology. In our evaluation, the factors in ![]() consist of samples
that yield four types of workloads: SPECsfs97, Web server, Mail server, and
DB_TP (Section 5.2). The controller uses Fstress to generate
samples of
consist of samples
that yield four types of workloads: SPECsfs97, Web server, Mail server, and
DB_TP (Section 5.2). The controller uses Fstress to generate
samples of ![]() that correspond to these workloads. We report results for
a single factor in
that correspond to these workloads. We report results for
a single factor in ![]() : the number of disks attached to the NFS server in
: the number of disks attached to the NFS server in
![]() , and a single factor in
, and a single factor in ![]() : the number of
nfsd daemons for the NFS server chosen from
: the number of
nfsd daemons for the NFS server chosen from
![]() to give us a total of
to give us a total of ![]() samples.
samples.
The workbench tools can generate both virtual and physical machine
configurations automatically. In our evaluation we use physical machines that
have ![]() MB memory,
MB memory, ![]() GHz x86 CPU, and run the
GHz x86 CPU, and run the ![]() Linux kernel. To
conduct an experiment, the workbench controller first prepares an experiment by
generating a sample in
Linux kernel. To
conduct an experiment, the workbench controller first prepares an experiment by
generating a sample in
![]() . It then
consults the benchmarking policy(ies) in
Sections 3.4-4 to plot a response surface and/or
search for the peak rate for a given sample with target confidence and accuracy.
. It then
consults the benchmarking policy(ies) in
Sections 3.4-4 to plot a response surface and/or
search for the peak rate for a given sample with target confidence and accuracy.
|
We use Fstress to generate ![]() corresponding to four workloads as
summarized in Table 3. A brief summary follows. Further
details are in [1].
corresponding to four workloads as
summarized in Table 3. A brief summary follows. Further
details are in [1].
For evaluating the overall methodology and the policies outlined in
Sections 3.3 and 4, we define the peak rate
![]() to be the test load that causes: (a) the mean server response time
to be in the
to be the test load that causes: (a) the mean server response time
to be in the ![]() ms region; or (b) the 95-percentile request response time
to exceed
ms region; or (b) the 95-percentile request response time
to exceed ![]() ms to complete. We derive the
ms to complete. We derive the ![]() region by choosing mean
server response time threshold at the peak rate
region by choosing mean
server response time threshold at the peak rate ![]() to be
to be ![]() ms and the
width factor
ms and the
width factor ![]() in Table 2. For all results except where
we note explicitly, we aim for a
in Table 2. For all results except where
we note explicitly, we aim for a ![]() to be accurate within
to be accurate within ![]() % of its
true value with
% of its
true value with ![]() % confidence.
% confidence.
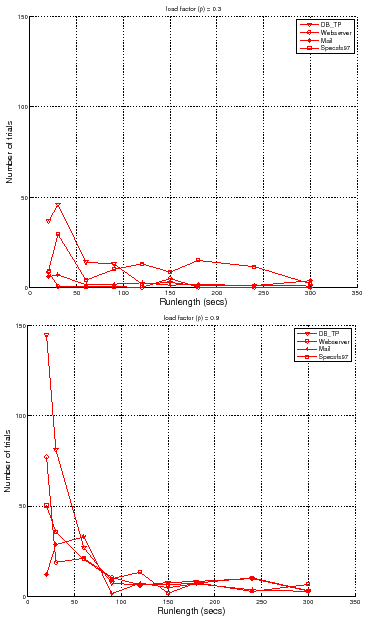
Figure 7 shows the choice of load factors for finding
the peak rate for a sample with ![]() disks and
disks and ![]() nfsds using the policies
outlined in Section 4. Each point on the curve represents a
single trial for some load factor. More points indicate higher number of trials
at that load factor. For brevity, we show the results only for DB_TP.
Other workloads show similar behavior.
nfsds using the policies
outlined in Section 4. Each point on the curve represents a
single trial for some load factor. More points indicate higher number of trials
at that load factor. For brevity, we show the results only for DB_TP.
Other workloads show similar behavior.
For all policies, the controller conducts more trials at load factors near
![]() than at other load factors to find the peak rate with the target accuracy
and confidence. All policies without seeding start at a low load factor and take
longer to reach a load factor of
than at other load factors to find the peak rate with the target accuracy
and confidence. All policies without seeding start at a low load factor and take
longer to reach a load factor of ![]() as compared to policies with
seeding. All policies with seeding start at a load factor close to
as compared to policies with
seeding. All policies with seeding start at a load factor close to ![]() , since
they use the peak rate of a previous sample with
, since
they use the peak rate of a previous sample with ![]() disks and
disks and ![]() nfsds as the
seed load.
nfsds as the
seed load.
Linear takes a significantly longer time because it uses a fixed
increment by which to increase the test load. However, Binsearch jumps to
the peak rate region in logarithmic number of steps. The Model policy is
the quickest to jump near the load factor of ![]() , but incurs most of its cost
there. This happens because the model learned is sufficiently accurate for
guiding the search near the peak rate, but not accurate enough to search
the peak rate quickly.
, but incurs most of its cost
there. This happens because the model learned is sufficiently accurate for
guiding the search near the peak rate, but not accurate enough to search
the peak rate quickly.
 |
We also observe that Binsearch, Binsearch with Seeding, and Linear with Seeding are robust across the workloads, but the model-guided policy is unstable. This is not surprising given that the accuracy of the learned model guides the search. As Section 3.6 explains, if the model is inaccurate the search may converge slowly.
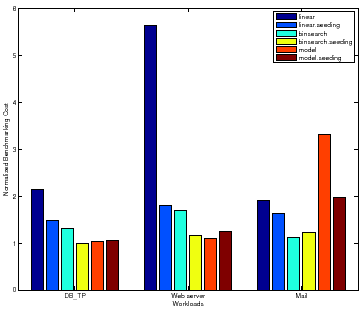
The linear policy is inefficient and highly sensitive to the magnitude of peak
rate. The benchmarking cost of Linear for Web server peaks at a
higher absolute value for all samples than for DB_TP and Mail,
causing more than a factor of ![]() increase in the total cost for mapping the
surface. Note that for Mail, Binsearch with Seeding incurs a
slightly higher cost than Binsearch. For some configurations, as
Section 3.7 explains, seeding can incur additional cost to recover
from a bad seed resulting in longer search times.
increase in the total cost for mapping the
surface. Note that for Mail, Binsearch with Seeding incurs a
slightly higher cost than Binsearch. For some configurations, as
Section 3.7 explains, seeding can incur additional cost to recover
from a bad seed resulting in longer search times.
 |
Reducing the Number of Samples. To evaluate the RSM approach presented in
Section 4, we approximate the response surface by a
quadratic curve in two dimensions: peak rate = func(number of disks, number of
nfsds). We use a D-optimal design [17] from RSM to obtain the best
of ![]() ,
, ![]() and
and ![]() samples out of a total of
samples out of a total of ![]() samples for learning the
response surface equation. We use Binsearch to obtain the
peak rate for each.
samples for learning the
response surface equation. We use Binsearch to obtain the
peak rate for each.
After learning the equation, we use it to predict the peak rate at all the other samples in the surface. Table 4 presents the mean absolute percentage error in predicting the peak rate across all the samples. The results show that D-optimal designs do a very good job of picking appropriate samples, and that very little more can be learned by small increases in the number of points sampled. Improving the accuracy of the surface with limited numbers of sampled points is an area of ongoing research.
|
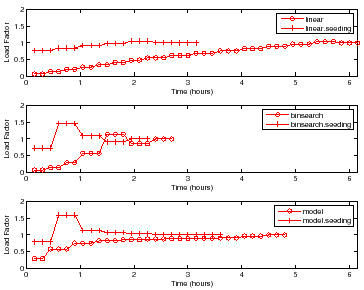
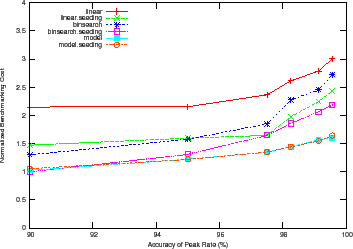
Figure 9 shows how the benchmarking methodology adapts the total benchmarking cost to the target confidence and accuracy of the peak rate. The figure shows the total benchmarking cost for mapping the response surface for the DB_TP using the Binsearch policy for different target confidence and accuracy values.
Higher target confidence and accuracy incurs higher benchmarking cost. At
![]() % accuracy, note the cost difference between the different confidence
levels. Other workloads and policies exhibit similar behavior, with Mail incurring a normalized benchmarking cost of
% accuracy, note the cost difference between the different confidence
levels. Other workloads and policies exhibit similar behavior, with Mail incurring a normalized benchmarking cost of ![]() at target accuracy of
at target accuracy of
![]() % and target confidence of
% and target confidence of ![]() %.
%.
 |
So far, we configure the target accuracy of the peak rate by configuring the
accuracy, ![]() , of the response time at the peak rate. The width parameter
, of the response time at the peak rate. The width parameter ![]() also controls the accuracy of the peak rate (Table 2) by
defining the peak rate region. For example,
also controls the accuracy of the peak rate (Table 2) by
defining the peak rate region. For example, ![]() % implies that if the mean
server response time at a test load is within
% implies that if the mean
server response time at a test load is within ![]() % of the threshold mean
server response time,
% of the threshold mean
server response time, ![]() , then the controller has found the peak rate. As
the region narrows, the target accuracy of the peak rate region increases. In
our experiments so far, we fix
, then the controller has found the peak rate. As
the region narrows, the target accuracy of the peak rate region increases. In
our experiments so far, we fix ![]() %.
%.
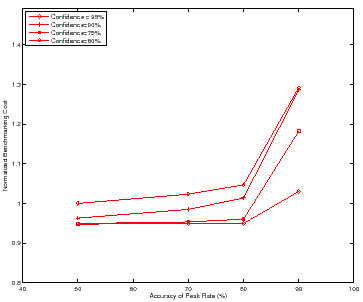
Figure 10 shows the benchmarking cost adapting to the target
accuracy of the peak rate region for different policies at a fixed target
confidence interval for DB_TP (![]() ) and fixed target accuracy of
the mean server response time at the peak rate (
) and fixed target accuracy of
the mean server response time at the peak rate (![]() %). The results for
other workloads are similar. All policies except the model-guided policy incur
the same benchmarking cost near or at the peak rate since all of them do binary
search around that region. Since a narrower peak rate region causes more trials
at or near load factor of
%). The results for
other workloads are similar. All policies except the model-guided policy incur
the same benchmarking cost near or at the peak rate since all of them do binary
search around that region. Since a narrower peak rate region causes more trials
at or near load factor of ![]() , the cost for these policies converge.
, the cost for these policies converge.
 |
Several researchers have made a case for statistically significant results from system benchmarking, e.g., [4]. Auto-pilot [26] is a system for automating the benchmarking process: it supports various benchmark-related tasks and can modulate individual experiments to obtain a target confidence and accuracy. Our goal is to take the next step and focus on an automation framework and policies to orchestrate sets of experiments for a higher level benchmarking objective, such as evaluating a response surface or obtaining saturation throughputs under various conditions. We take the workbench test harness itself as given, and our approach is compatible with advanced test harnesses such as Auto-pilot.
While there are large numbers and types of benchmarks, (e.g., [5,14,3,15]) that test the performance of servers in a variety of ways, there is a lack of a general benchmarking methodology that provides benchmarking results from these benchmarks efficiently with confidence and accuracy. Our methodology and techniques for balancing the benchmarking cost and accuracy are applicable to all these benchmarks.
Zadok et al. [25] present an exhaustive nine-year study of file system and storage benchmarking that includes benchmark comparisons, their pros and cons [22], and makes recommendations for systematic benchmarking methodology that considers a range of workloads for benchmarking the server. Smith et al. [23] make a case for benchmarks the capture composable elements of realistic application behavior. Ellard et al. [10] show that benchmarking an NFS server is challenging because of the interactions between the server software configurations, workloads, and the resources allocated to the server. One of the challenges in understanding the interactions is the large space of factors that govern such interactions. Our benchmarking methodology benchmarks a server across the multi-dimensional space of workload, resource, and configuration factors efficiently and accurately, and avoids brittle "claims" [16] and "lies" [24] about a server performance.
Synthetic workloads emulate characteristics observed in real environments. They are often self-scaling [5], augmenting their capacity requirements with increasing load levels. The synthetic nature of these workloads enables them to preserve workload features as the file set size grows. In particular, the SPECsfs97 benchmark [6] (and its predecessor LADDIS [15]) creates a set of files and applies a pre-defined mix of NFS operations. The experiments in this paper use Fstress [1], a synthetic, flexible, self-scaling NFS workload generator that can emulate a range of NFS workloads, including SPECsfs97. Like SPECsfs97, Fstress uses probabilistic distributions to govern workload mix and access characteristics. Fstress adds file popularities, directory tree size and shape, and other controls. Fstress includes several important workload configurations, such as Web server file accesses, to simplify file system performance evaluation under different workloads [23] while at the same time allowing standardized comparisons across studies.
Server benchmarking isolates the performance effects of choices in server design and configuration, since it subjects the server to a steady offered load independent of its response time. Relative to other methodologies such as application benchmarking, it reliably stresses the system under test to its saturation point where interesting performance behaviors may appear. In the storage arena, NFS server benchmarking is a powerful tool for investigation at all layers of the storage stack. A workload mix can be selected to stress any part of the system, e.g., the buffering/caching system, file system, or disk system. By varying the components alone or in combination, it is possible to focus on a particular component in the storage stack, or to explore the interaction of choices across the components.
This paper focuses on the problem of workbench automation for server benchmarking. We propose an automated benchmarking system that plans, configures, and executes benchmarking experiments on a common hardware pool. The activity is coordinated by an automated controller that can consider various factors in planning, sequencing, and conducting experiments. These factors include accuracy vs. cost tradeoffs, availability of hardware resources, deadlines, and the results reaped from previous experiments.
We present efficient and effective controller policies that plot the saturation throughput or peak rate over a space of workloads and system configurations. The overall approach consists of iterating over the space of workloads and configurations to find the peak rate for samples in the space. The policies find the peak rate efficiently while meeting target levels of confidence and accuracy to ensure statistically rigorous benchmarking results. The controller may use a variety of heuristics and methodologies to prune the sample space to map a complete response service, and this is a topic of ongoing study.