| Technique | Benefits |
| Tree set planning (Section 3)
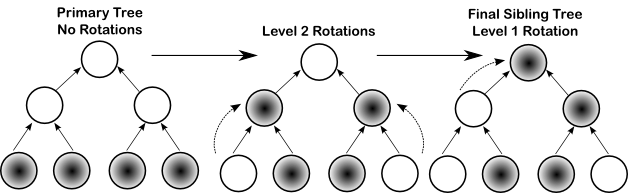
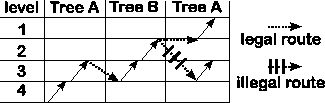
| A primary static overlay tree places the majority of data
close to the root operator by clustering network coordinates. Static
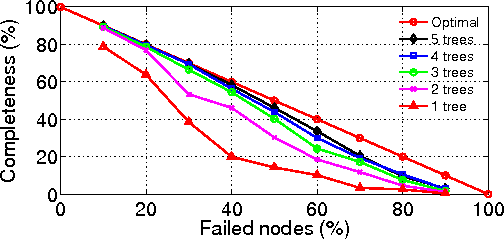
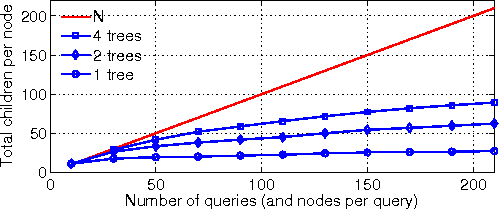
sibling trees preserve the network awareness of the primary, while exhibiting the path diversity of random trees.
|
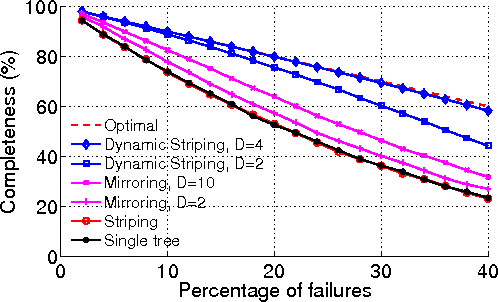
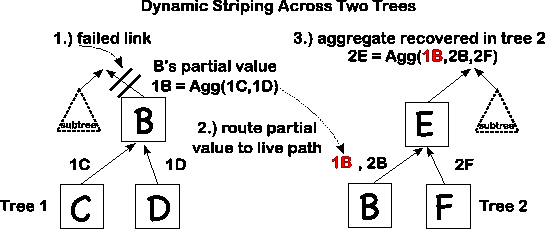
| Dyamic tuple striping (Section 3.3)
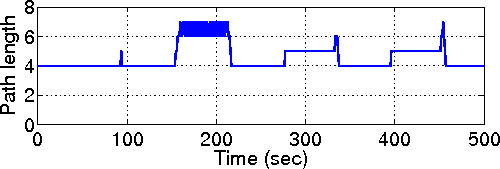
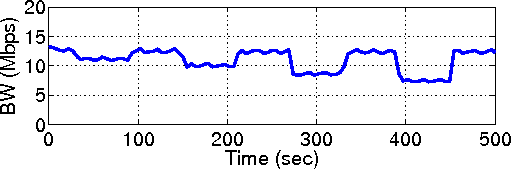
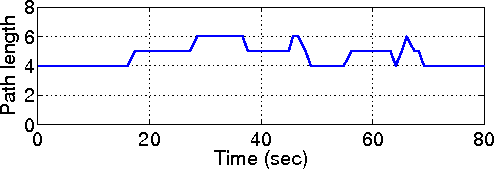
| Route tuples toward root operator while leveraging
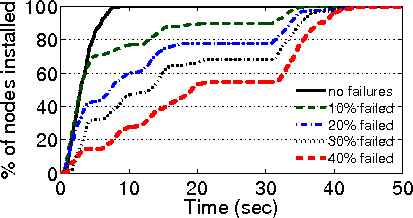
available paths. Ensures low path length and avoids cycles. Even when 40% of the nodes
are unreachable, data from 94% of the remaining nodes is available.
|
| Time-division data partitioning (Section 4)
| Isolates tuple processing from tuple routing, allowing
multipath tuple routing, and avoiding duplicate data processing.
|
| Syncless operation (Section 5)
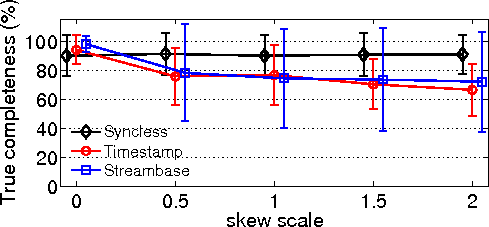
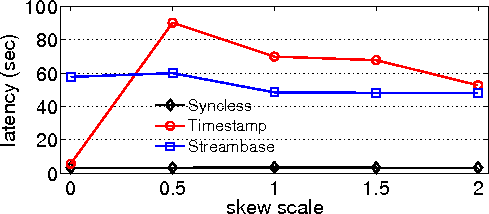
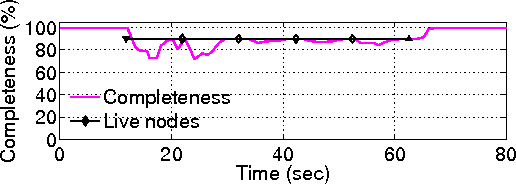
| Allows accurate stream processing in the presense of
relative clock offset, and reduces result latency by a factor
of 8.
|
| Pair-wise reconciliation (Section 6)
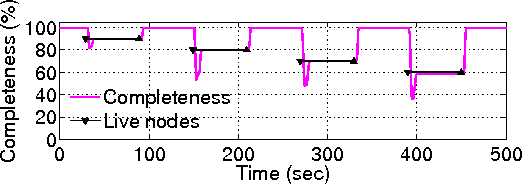
| Leverages combined connectivity of D overlay trees for eventually consistent query installation and removal.
|