
HiLighter: Automatically Building Robust Signatures of
Performance Behavior for Small- and Large-Scale Systems
Peter Bodík1, Moises Goldszmidt2, Armando Fox1
|
1RAD Lab, EECS Department, UC Berkeley, | 2Microsoft Research, Silicon Valley |
|
|
November 22, 2008
Abstract
Previous work showed that statistical analysis techniques could
successfully be used to construct compact signatures of
distinct operational problems in Internet server systems. Because
signatures are amenable to well-known
similarity search techniques, they can be used as a way to index past
problems and identify particular operational problems as new or
recurrent. In this paper we use a different statistical technique for
constructing signatures (logistic regression with L1 regularization)
that improves on previous work in two ways. First, our new approach
works for cases where the number of features is an order of magnitude
larger than the number of samples and also scales to
problems with over 50,000 samples.
Second, we
get encouraging results regarding the stability of the models and the signatures
by cross-validating the accuracy of the models from one section
of the data center on another section.
We validate our approach on
data from an Internet service testbed and also from a production enterprise
system comprising hundreds of servers in several data centers.
Interactive network services experience performance problems for a wide variety of reasons. Diagnosing these
problems is complicated due to various factors including the large scale deployment of these services, their
complex interactions, and the large number of metrics collected in each component of the system.
The work in [2] proposed an approach to alleviate the
diagnosis problem by automatically building a compact signature of each
failure mode. These signatures are then used to a) localize the problem
(sometimes establishing a path to the root cause), b) detect recurring instances
of the same problem, and c) serve as indexes for annotations regarding
resolution. The applications b) and c) were addressed using a similarity search
over the signatures, effectively reducing problem identification to information
retrieval. The automatic construction of these signatures
in [2] is based on classification with feature selection to
find subsets of measured system metrics (CPU, memory utilization, etc.) that were
correlated with the performance problem. The signature of a particular instance
of a problem is then extracted by finding whether each of the selected features
contributes to classifying the instance as anomalous or as normal. The paper then
demonstrated the benefits of this approach on a transactional system consisting
of tens of geographically-distributed servers.
In this paper we revise the methodology for inducing a classifier and selecting the features. While the work
in [2] relied on a Bayesian network classifier and a heuristic search over the space of
features, we use logistic regression with L1
regularization [6][7]. The first advantage
of using this approach is that it works well in cases where the number of features being considered exceeds
the number of samples; Case Study 1 describes an example with over 2000
features and only 86 datapoints. An example of such a scenario is application
testing, where thousands of features are collected per machine, yet the number of samples in a particular
failure mode is limited by the duration of the test run. The second
advantage is the availability of very efficient implementations of L1-regularized regression that scale to
datasets with tens of thousand samples, which is a requirement
for an application in a cloud computing environment with thousands of machines. We built a tool called HiLighter based on the algorithm and C#
implementation for regularized log-linear models described in [1].
To demonstrate and validate HiLighter we applied it to data from a testbed of an
Internet service, where the number of features is an order of magnitude higher
than the number collected samples. This testbed is used in the service product
group to test and validate new features in the product. We also applied HiLighter
to data from two known performance problems in a production environment with
hundreds of machines, each reporting hundreds of metrics. Three interesting
results emerge. First, we were able to help diagnose a problem in the testbed
using HiLighter. This is notable since the approach in [2]
would be unable to reliably fit a model under those conditions. Second, we get
encouraging results by cross-validating the accuracy of the models from one group
of servers in a datacenter on a new group of servers. Given that the signatures
are extracted from the models in a deterministic fashion, the results suggest
that the signatures being computed as "digests" of the problem states are
stably capturing the metrics relevant to each problem. Finally, we observe
stable and distinct signatures for the system's state just before and
after the performance problem as well. This suggests that signatures can be used
not only to identify a particular performance problem but possibly to forecast it
almost an hour in advance. We are currently working with human experts on
verifying the forecasting possibilities. The group responsible for the service
whose data was analyzed have incorporated the code for HiLighter to their code
tree for integration with their other tools.
We first present the details of the HiLighter algorithm, followed by three case
studies: one from an application testbed and two from a large-scale production
environment.
We start by reviewing the classification model and feature selection approach
used by HiLighter and then we contrast these with the approaches
in [2]. HiLighter is based on a logistic regression
classifier. A logistic regression model is a common statistical parametric
approach based on the assertion that the class variable Y is a Bernoulli random
variable with mean pj [8], where 1 <= j <= m is the jth
sample.1 Given the set of features M, the
model is given by
p_j = P(Y_j = 1|M_j = m) = (exp(SUM_i beta_i m_i))/(1+ exp(SUM_i
beta_i m_i))
Usually, the parameters betai are fitted by maximizing the
likelihood function L(beta) = PRODj pjYj(1-pj)1-Yj.
The L1 regularization extends the objective function to include the
constraint that the L1 norm of the parameters be less than a value
lambda; that is, SUM|betai| <= lambda, where lambda can be
fitted in a variety of ways including cross-validation. Because the first partial derivative of the L1 regularizer with respect to each
beta coefficient is constant as the coefficient moves toward zero, the values
of the coefficients are "pushed" all the way to zero if possible. For more formal
justifications we refer the reader to [7][6][1]. This
regularization was shown theoretically and experimentally to learn good models
even when most features are irrelevant and when the number of parameters is
comparable to the number of samples [7][6]. It also typically produces
sparse coefficient vectors in which many of the coefficients are exactly zero
and can thus be used for feature selection.
In contrast, the feature selection approach in [2] was based
on a greedy search process wrapped around an induction of a Bayesian network
classifier [4], which has two immediate consequences. First, because the
search considers changes to one feature at a time in a greedy neighborhood, the
explored search space is severly constrained and in large problems only a small
subspace is explored. Second, the inner loop of the feature selection requires a
model selection step such as cross-validation which introduces another source of
error.2 By relying on the gradient of the likelihood function, the logistic
regression with L1 regularization performs a guided exploration of a much larger
part of the search space.
We adapt the methodology in [2] to our setting to construct
signatures of performance problems. In each time quantum, the system
collects hundreds of performance metrics reported by the hardware, operating
system (Windows Server), runtime system (Microsoft Common Language Runtime), and
the application itself. The operators of the service specify one of these
performance metrics as a "metric of merit" (e.g., average response time) and we
define a class for each time interval as normal or abnormal, depending on whether
the metric of merit exceeds some chosen threshold during that interval.
The first step in constructing the signatures for a performance anomaly is a
selection of a small number of metrics that well predict both normal and abnormal
performance with high accuracy. HiLighter transforms the measured metrics using
standard preprocessing: a) removes the constant metrics, b) augments each metric
by computing a gradient and standard deviation with respect to one or two time
periods in the past (thereby creating additional features), and c) normalizes the
metrics to zero mean and variance of one. For now, we simply remove entries for
which data is missing; this was not a factor in Case Study 1, but it affected
Case Study 2, as described in Section *.
As recommended in [2], we evaluate the models using Balanced
Accuracy, which averages the probability of correctly classifying normal
with probability of detecting an anomaly; this is necessary since there
are typically many more instances of normal performance than anomalous
performance. The number of metrics selected is affected by a lambda parameter
which is the contraint on the L1 regularization. There are many ways to find
lambda that achieves the optimal classification
accuracy [9]; HiLighter uses five-fold cross-validation in
conjunction with a binary search over the values of lambda.
After the feature selection using L1, HiLighter fits the final model using the
selected metrics and adds an L2 constraint to stabilize for correlated features
(as recommended in [9]). HiLighter then reports balanced
accuracy, the confusion matrix including false positives and false negatives, and
the balanced accuracy of using each metric alone as a classifier. As will be
apparent in Case Study 2 and 3, the balanced accuracy of the final model with
multiple metrics is significantly better than the balanced accuracy of a model
with just one or two metrics, clearly making the case for models that take into
account the interaction among features.
Finally, we use the selected metrics to construct a signature of each machine at
each time interval. A signature consists of the list of the selected metrics,
where we label each metric as abnormal if its value
contributes positively to the classification of this machine as abnormal; otherwise we label
the metric normal. Formally, metric i is labeled abnormal if
mi * betai > 0, where mi is the value of metric i and betai is the
coefficient in the linear classifier corresponding to this metric. Such a
signature serves as a condensed representation of the state of the machine at
the given time interval.
The first case study concerns a multi-tier Internet application
deployed across multiple datacenters. We examined traces from a
small-scale testbed used for testing new features and capabilities of
the application. The traces contained the following types of metrics
measured every 30 seconds: workload, response times, OS-level metrics,
.NET runtime metrics, and application-specific metrics.
After the feature extraction process in HiLighter, the dataset
contained about 1000 features per server.
The performance anomaly we investigated was large variance in the
99th percentile of latency under steady workload and stable external
environment. The values of latency were ranging from 50 to 1200 ms, in clear
contrast to an identical run on a separate set of servers where the response time
stayed below 300 ms. We found that a threshold of 400 ms clearly separated the
slow, anomalous requests from the normal ones. We included metrics from one
first-tier and one second-tier server, since each request passed through both
types of server. The resulting dataset contained only 86 datapoints and 2008
features, from which HiLighter selected just two metrics, both reported by the
.NET runtime: number of induced garbage collections and change in number of
allocated bytes. The resulting model reached cross-validated balanced accuracy of
0.94 which strongly suggests that garbage collection was the cause of this
performance anomaly. We note that we tried all major classifiers, including Naive
Bayes and Support Vector Machines, with feature selection as implemented in
Weka [5] with little success.
The second case study focuses on a performance issue in the production version of
another large-scale Internet application. This application is deployed across six
datacenters with hundreds of servers, each serving one of five roles in the
overall application. The "application core" servers--call them Role 1
servers--contain the main application logic, and each of these servers measures
the average latency of requests it processed. The performance problem we
investigated was triggered by a deployment of a bad configuration file to all
Role 1 servers, resulting in significant processing delays of the received
requests.
We used HiLighter on data from four groups of Role 1 servers housed in
datacenter 5; each group contained between 20 and 70 servers. The feature
extraction process resulted in a dataset with approximately 500 metrics and 100
datapoints per server and time interval. We used the average latency on each
server as our reference metric and used a threshold supplied by operators of this
service. The linear models produced by HiLighter selected between six and nine
metrics and achieved cross-validated balanced accuracy between 0.92 and 0.95. The
selected metrics were a combination of CPU utilization, internal workloads, and
other application-specific measures. When comparing models that used exactly six
metrics, five of the metrics selected by the different models were identical,
thus, the models would generate almost identical signatures. The number of
metrics selected can heavily influence model accuracy: in one group of servers,
the balanced accuracy increased from 0.83 with only two metrics to 0.92 with six
metrics, further confirming the need to consider interactions among metrics
rather than just the contributions of individual metrics.
Despite using data from the same anomaly, there were notable differences in the
metrics selected for each model. These differences could mean that the models
wouldn't generalize to other instances of this anomaly, which would decrease
their usefulness. To test the accuracy of the models on new instances of this
anomaly, we separately evaluated each of the models on data from the remaining
three groups of servers. As summarized in Table *, the balanced
accuracy was between 0.90 and 0.96 which demonstrates that the models could
accurately detect this anomaly. We believe that the differences in selected
metrics are due to missing values in our dataset; we omitted metrics with too
many values missing and these thus couldn't be selected by HiLighter. Later the
operators of the service informed us that the missing data points actually
represent a values of zero. After replacing the missing values with zeros, the
metrics selected in different groups of servers were almost identical.
Knowing which other server roles were affected by this anomaly could considerably
help the operators during root cause analysis. We therefore used HiLighter on the
other four types servers (roles two through five) grouped by datacenter and role.
However, because these servers don't measure latency as the role 1 servers do, we
used timestamps to define the anomaly. That is, the anomaly is defined to have
occurred during the time period in which the role 1 servers were reporting poor
request latency.
As summarized by Table *, for some groups of servers, such as
role 5 in datacenter 6, the balanced accuracy was very low, suggesting that
(metrics reported by) these servers were not affected by this issue. However,
most of the other server groups seem to have been affected and analyzing the
selected metrics would likely aid the operators in diagnosing this issue.
We constructed signatures as defined in Section * for a group
of 71 servers and analyzed how these signatures evolved before, during, and after
the anomaly (see Figure *). HiLighter selected six metrics for
the model: three measures of CPU utilization (features 1-3), number of
connections and disconnections on an internal component in the server (features
4-5), and the variance of workload on another internal component (feature 6). As
described in Section *, given a model of the anomaly, a
signature is constructed for every data point, i.e. for each server and time
interval. The signature consists of the metrics selected for the model and a
binary label for each metric. A + label means that the value of the metric
is abnormal relative to the model, a - label means the metric is
normal.
The changes in signatures over time help us understand what happened during the
anomaly. To simplify the visualization of signatures in
Figure *, we clustered the signatures into four groups based on
the number of abnormal metrics. Signature group A (dark gray) contains
signatures with at most two abnormal metrics; signature B (light gray) has
all metrics abnormal except metric 6; signature C (black) has all metrics
abnormal; and group other represents all remaining signatures. The
figure clearly shows that signatures in group A were prevalent up to about 14
intervals before the start of the anomaly and then again 14 intervals after the
end of the anomaly. Despite containing some anomalous metrics, the HiLighter
model correctly predicted normal. Signature C corresponds to the anomaly
itself, and since all the metrics are anomalous, the model correctly predicted
anomaly. However, up to 14 intervals before and after the anomaly,
signature B was most prevalent, which suggests that five out of the six chosen
metrics were already "misbehaving" long before the measured anomaly started.
The anomaly of individual metrics caused a significant number of false positives
in the results of the HiLighter model. We hypothesize that further characterizing
signature B would allow us to predict such anomalies in the future.
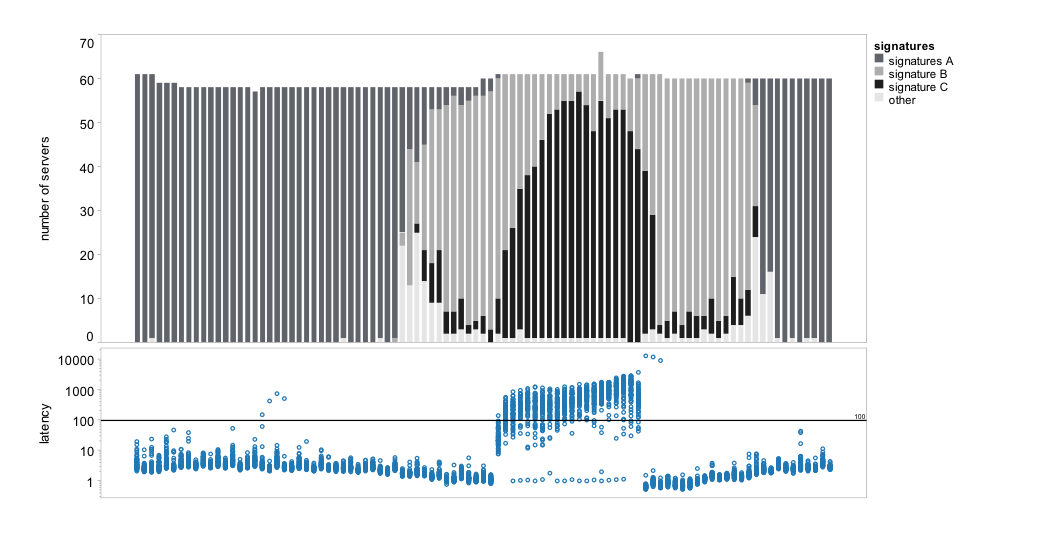 The bottom plot shows the latency as measured by the 71 role-one servers over time; each dot represents latency on one server during a single time interval. The anomaly is visible in the middle part of the plot. The top plot shows the evolution of signatures over time on all the servers; on average, for ten out of the 71 servers we cannot compute signatures because of missing values.
The bottom plot shows the latency as measured by the 71 role-one servers over time; each dot represents latency on one server during a single time interval. The anomaly is visible in the middle part of the plot. The top plot shows the evolution of signatures over time on all the servers; on average, for ten out of the 71 servers we cannot compute signatures because of missing values.
|
| gr. 1 | gr. 2 | gr. 3 | gr. 4 |
|
group 1 | 0.92 | 0.93 | 0.92 | 0.91 |
|
group 2 | 0.95 | 0.95 | 0.96 | 0.94 |
|
group 3 | 0.92 | 0.92 | 0.95 | 0.92 |
|
group 4 | 0.90 | 0.90 | 0.92 | 0.93 |
|
|
Results for case study 2 (configuration issue) for servers in role 1 in datacenter 5; each cell shows balanced accuracy of a model trained on the group of servers specified in the row header and evaluated on the group specified in the column header. Entries along the diagonal represent the cross-validation results.
|
| DC 1 | DC 2 | DC 3 | DC 4 | DC 5 | DC 6 |
|
role 1 | 0.92 | 0.95 | 0.99 | | 0.92 | |
|
role 2 | 0.96 | 0.99 | 0.85 | 0.67 | 0.97 | |
|
role 3 | | | | 0.93 | | |
|
role 4 | | | | | | 0.80 |
|
role 5 | | | | 1.00 | | 0.52 |
|
|
Each cell shows the cross-validated balanced accuracy for case study 2 (configuration issue) for servers in all roles in all datacenters. This might help localize the source the problem. Note: not all datacenters contain servers of all roles.
|
| gr. 1 | gr. 2 | gr. 3 | gr. 4 |
|
group 1 | 0.97 | 0.97 | 0.96 | 0.96 |
|
group 2 | 0.98 | 0.99 | 0.98 | 0.98 |
|
group 3 | 0.96 | 0.95 | 0.99 | 0.99 |
|
group 4 | 0.95 | 0.92 | 0.96 | 0.96 |
|
|
Results for case study 3 (overloaded datacenter) for servers in role 1 in datacenter 5; each cell shows balanced accuracy of a model trained on the group of servers specified in the row header and evaluated on the group specified in the column header. Entries along the diagonal represent the cross-validation results.
In the last case study we analyze another performance issue in the same
application. One of its datacenters was overloaded, which caused significant
processing delays as external traffic was redirected to the remaining
datacenters. After feature extraction we obtained a dataset of approximately 500
features and 100 datapoints per server. We used HiLighter on the same four groups
of Role 1 servers as in Case Study 2, and evaluated each model on data from the
remaining three groups. As summarized in Table *, with one
exception, accuracy of the models was in the range of 0.95 and 0.99. Three
out of the four metrics selected by the different models were identical and
thus the models would generate almost identical signatures.
As in Case Study 2, we analyzed the evolution of the signatures for the
group of 71 Role 1 servers. The HiLighter model selected for this group of
servers includes CPU utilization (feature 1) and variance of four internal
workload metrics (features 2-5). Figure * shows the behavior
over time (normal vs. abnormal with respect to the performance model) of the five
individual features. This visualization allows us to easily spot when each
metric became abnormal and how many servers were affected. Metrics 2, 3 and 5
capture the duration of the anomaly very well, but the anomaly in CPU utilization
(metric 1) precedes the start of the performance issue. We hypothesize that this
signature could be used in the future to predict the occurrence of such
anomalies. One troublesome issue is the behavior of metric 4, which becomes
abnormal long before the anomaly starts. However, since it is the only
anomalous metric, HiLighter's model correctly predicts normal overall
state of the system, and reports only a single false negative at the beginning of
the dataset.
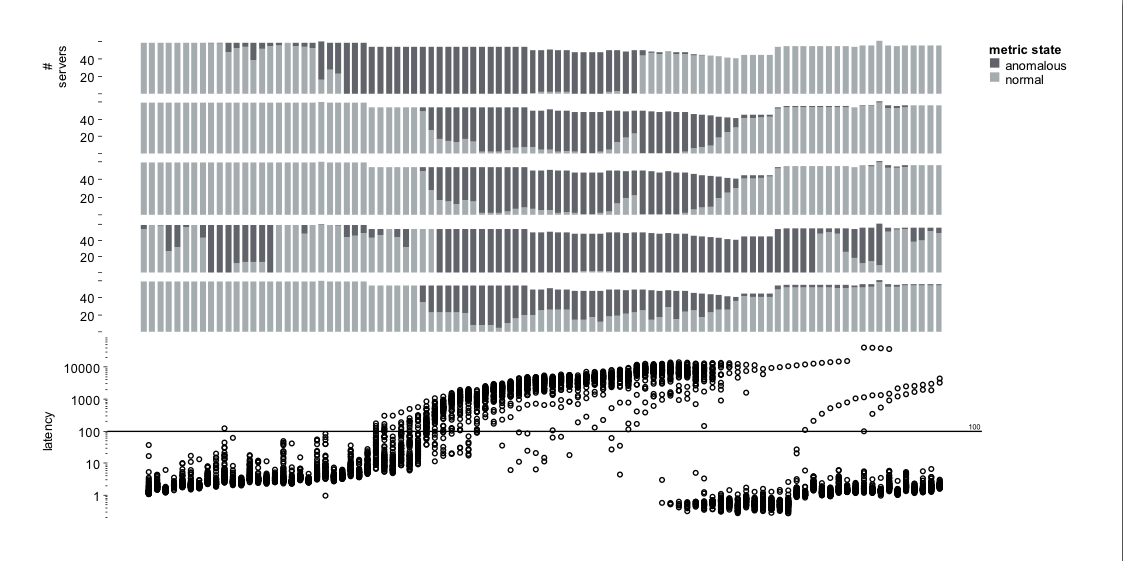 As in Figure *, the bottom plot shows the latency on the 71 role-one servers. The plots on the top show the state of each of the selected five metrics on these servers. Dark gray means that the value of the particular metric was abnormal with respect to the HiLighter model.
As in Figure *, the bottom plot shows the latency on the 71 role-one servers. The plots on the top show the state of each of the selected five metrics on these servers. Dark gray means that the value of the particular metric was abnormal with respect to the HiLighter model.
HiLighter is being incorporated into a set of tools used by the test
team responsible for the application in Case Study 1. It is also
part of the diagnostic tool Artemis [3] for finding bugs and
performance problems in large clusters of machines where DryadLINQ [10] (or Map
Reduce) parallel programs are executed.
HiLighter's performance on the datasets we examined
strongly suggests that the methodology of
logistic regression with L1 regularization produced robust models in scenarios with large
numbers of features and only few datapoints, as well as in cases of
multi-datacenter applications with hundreds of machines and large data
sets. The work is still in progress: we are currently validating the
results and confirming the benefits of the signatures found.
This is important given the evidence that the "synthesized"
features, such as the rates computed in Case Study 1 and the variances
computed in Case Studies 2 and 3, contribute critically to the balanced
accuracy of the models and the stability of the
constructed signatures. Thus, we would like to encourage the addition of
new features (based on the measured metrics) so that engineers could add
knowledge about the domain without being constrained by the
characteristics of the model building process.
- [1]
-
G. Andrew and J. Gao.
Scalable training of L1-regularized log-linear models.
In Z. Ghahramani, editor, Proceedings of the 24th Annual
International Conference on Machine Learning (ICML 2007), pages 33-40.
Omnipress, 2007.
- [2]
-
I. Cohen, S. Zhang, M. Goldszmidt, J. Symons, T. Kelly, and A. Fox.
Capturing, indexing, clustering, and retrieving system history.
In A. Herbert and K. P. Birman, editors, SOSP, pages 105-118.
ACM, 2005.
- [3]
-
G. Cretu, M. Budiu, and M. Goldszmidt.
Hunting for problems with Artemis.
Technical report, Microsoft, 2008.
- [4]
-
N. Friedman, D. Geiger, and M. Goldszmidt.
Bayesian network classifiers.
Mach. Learn., 29(2-3):131-163, 1997.
- [5]
-
S. R. Garner.
Weka: The Waikato Environment for Knowledge Analysis.
In In Proc. of the New Zealand Computer Science Research
Students Conference, pages 57-64, 1995.
- [6]
-
K. Koh, S.-J. Kim, and S. Boyd.
An interior-point method for large-scale L1-regularized logistic
regression.
Journal of Machine Learning Research, 8:1519-1555, 2007.
- [7]
-
A. Ng.
Feature selection, L1 vs. L2 regularization, and rotational
invariance.
In Proceedings of the 21st Annual International Conference on
Machine Learning (ICML 2004), 2004.
- [8]
-
L. Wasserman.
All of statistics.
Springer, 2004.
- [9]
-
M. Young and P. T. Hastie.
L1 regularization path algorithm for generalized linear models, 2006.
- [10]
-
Y. Yu, M. Isard, D. Fetterly, M. Budiu, Ú. Erlingsson, P. K. Gunda, and
J. Currey.
DryadLINQ: A system for general-purpose distributed data-parallel
computing using a high-level language.
In Symposium on Operating System Design and Implementation
(OSDI), San Diego, CA, December 8-10 2008.
 The bottom plot shows the latency as measured by the 71 role-one servers over time; each dot represents latency on one server during a single time interval. The anomaly is visible in the middle part of the plot. The top plot shows the evolution of signatures over time on all the servers; on average, for ten out of the 71 servers we cannot compute signatures because of missing values.
The bottom plot shows the latency as measured by the 71 role-one servers over time; each dot represents latency on one server during a single time interval. The anomaly is visible in the middle part of the plot. The top plot shows the evolution of signatures over time on all the servers; on average, for ten out of the 71 servers we cannot compute signatures because of missing values.
 As in Figure
As in Figure