
| Robert Beverly
MIT CSAIL rbeverly@csail.mit.edu |
Karen Sollins
MIT CSAIL solins@csail.mit.edu |
We pose partitioning a b-bit Internet Protocol (IP) address space as a supervised learning task. Given (IP, property) labeled training data, we develop an IP-specific clustering algorithm that provides accurate predictions for unknown addresses in O(b) run time. Our method offers a natural means to penalize model complexity, limit memory consumption, and is amenable to a non-stationary environment. Against a live Internet latency data set, the algorithm outperforms IP-naïve learning methods and is fast in practice. Finally, we show the model's ability to detect structural and temporal changes, a crucial step in learning amid Internet dynamics.
Learning has emerged as an important tool in Internet system and application design, particularly amid increasing strain on the architecture. For instance, learning is used to great effect in filtering e-mail [12], mitigating attacks [1], improving performance [9], etc. This work considers the common task of clustering Internet Protocol (IP) addresses.
With a network oracle, learning is unnecessary and predictions of e.g. path performance or botnet membership, are perfect. Unfortunately, the size of the Internet precludes complete information. Yet the Internet's physical, logical and administrative boundaries [5,7] provide structure which learning can leverage. For instance, sequentially addressed nodes are likely to share congestion, latency and policy characteristics, a hypothesis we examine in §2.
A natural source of Internet structure is Border Gateway Protocol (BGP) routing data [11]. Krishnamurthy and Wang suggest using BGP to form clusters of topologically close hosts thereby allowing a web server to intelligently replicate content for heavy-hitting clusters [8]. However, BGP data is often unavailable, incomplete or at the wrong granularity to achieve reasonable inference. Service providers routinely advertise a large routing aggregate, yet internally demultiplex addresses to administratively and geographically disparate locations. Rather than using BGP, we focus on an agent's ability to infer network structure from available data.
Previous work suggests that learning network structure is effective in forming predictions in the presence of incomplete information [4]. An open question, however, is how to properly accommodate the Internet's frequent structural and dynamic changes. For instance, Internet routing and physical topology events change the underlying environment on large-time scales while congestion induces short-term variance. Many learning algorithms are not amenable to on-line operation in order to handle such dynamics. Similarly, few learning methods are Internet centric, i.e. they do not incorporate domain-specific knowledge.
We develop a supervised address clustering algorithm that
imposes a partitioning over a
b-bit IP address space. Given
training data that is sparse relative to the size of the ![]() space,
we form clusters such that addresses within a cluster share a property
(e.g. latency, botnet membership, etc.) with a statistical guarantee
of being drawn from a Gaussian distribution with a common mean. The
resulting model provides the basis for accurate predictions, in
O(b)
time, on addresses for which the agent is oblivious.
space,
we form clusters such that addresses within a cluster share a property
(e.g. latency, botnet membership, etc.) with a statistical guarantee
of being drawn from a Gaussian distribution with a common mean. The
resulting model provides the basis for accurate predictions, in
O(b)
time, on addresses for which the agent is oblivious.
IP address clustering is applicable to a variety of problems including service selection, routing, security, resource scheduling, network tomography, etc. Our hope is that this building block serves to advance the practical application of learning to network tasks.
This section describes the learning task, introduces network-specific terminology and motivates IP clustering by finding extant structural locality in a live Internet experiment.
Let
![]() be training data where each
be training data where each
![]() is an IP address and
is an IP address and ![]() is a corresponding real or
discrete-valued property, for instance latency or security reputation.
The problem is to determine a model
is a corresponding real or
discrete-valued property, for instance latency or security reputation.
The problem is to determine a model
![]() where
where ![]() minimizes the prediction error on newly observed IP values.
minimizes the prediction error on newly observed IP values.
Beyond this basic formulation, the non-stationary nature of network problems presents a challenging environment for machine learning. A learned model may produce poor predictions due to either structural changes or dynamic conditions. A structural change might include a new link which influences some destinations, while congestion dynamics might temporarily influence predictions.
In the trivial case, an algorithm can remodel the world by purging old information and explicitly retraining. Complete relearning is typically expensive and unnecessary when only a portion of the underlying environment has changed. Further, even if a portion of the learned model is stale and providing inaccurate results, forgetting stale training data may lead to even worse performance. We desire an algorithm where the underlying model is easy to update on a continual basis and maintains acceptable performance during updates. As shown in §3, these Internet dynamics influences our selection of data structures.
IPv4 addresses are 32-bit unsigned integers, frequently represented as four ``dotted-quad'' octets (A.B.C.D). IP routing and address assignment uses the notion of a prefix. The bit-wise AND between a prefix p and a netmask m denotes the network portion of the address (m effectively masks the ``don't care'' bits). We employ the common notation p/m as containing the set of b-bit IP addresses inclusive of:
We use latency as a per-IP property of interest to ground our discussion and experiments. One-way latency between two nodes is the time to deliver a message, i.e. the sum of delivery and propagation delay. Round trip time (RTT) latency is the time for a node to deliver a message and receive a reply.
To motivate IP address clustering, and demonstrate that learning is feasible, we first examine our initial hypothesis: sufficient secondary network structure exists upon which to learn. We focus on network latency as the property of interest, however other network properties are likely to provide similar structural basis, e.g. hop count, etc.
Let distance d
be the numerical difference between two addresses:
![]() . To understand the correlation between
RTT and d,
we perform active measurement to gather live data from
Internet address pairs. For a distance d,
we find a random pair of
hosts,
. To understand the correlation between
RTT and d,
we perform active measurement to gather live data from
Internet address pairs. For a distance d,
we find a random pair of
hosts,
![]() , which are alive, measurable and separated by d.
We then measure the RTT from a fixed measurement node to
, which are alive, measurable and separated by d.
We then measure the RTT from a fixed measurement node to ![]() and
and
![]() over five trials.
over five trials.
We gather approximately 30,000 data points. Figure
1 shows the relationship between address pair
distance and their RTT latency difference. Additionally, we include a
![]() distance that represents randomly chosen address pairs,
irrespective of their distance apart. Two random addresses have less
than a 10% chance of agreeing within 10% of each other. In
contrast, adjacent addresses (
distance that represents randomly chosen address pairs,
irrespective of their distance apart. Two random addresses have less
than a 10% chance of agreeing within 10% of each other. In
contrast, adjacent addresses (![]() ) have a greater than 80%
probability of similar latencies within 20%. The average
disagreement between nodes within the same class C (
) have a greater than 80%
probability of similar latencies within 20%. The average
disagreement between nodes within the same class C (![]() ) is less
than 15%, whereas nodes in different /8 prefixes disagree by 50% or
more.
) is less
than 15%, whereas nodes in different /8 prefixes disagree by 50% or
more.
Our algorithm takes as input a network prefix (![]() ) and
) and ![]() training
points (
training
points (
![]() ) where
) where ![]() are distributed within the prefix. The
initial input is typically the entire IP address space (
are distributed within the prefix. The
initial input is typically the entire IP address space (![]() )
and all training points.
)
and all training points.
Define split ![]() as inducing
as inducing ![]() partitions,
partitions,
![]() , on
, on ![]() . Then for
. Then for
![]() :
:
Let
![]() iff the address of
iff the address of ![]() falls within prefix
falls within prefix ![]() (Eq. 1). The general form of the algorithm is:
(Eq. 1). The general form of the algorithm is:
Before refining, we draw attention to several properties of the algorithm that are especially important in dynamic environments:
![]() Complexity: A natural means to penalize complexity.
Intuitively, clusters representing very specific prefixes, e.g. /30's, are likely over-fitting. Rather than tuning
traditional machine learning algorithms indirectly, limiting the
minimum prefix size corresponds directly to network generality.
Complexity: A natural means to penalize complexity.
Intuitively, clusters representing very specific prefixes, e.g. /30's, are likely over-fitting. Rather than tuning
traditional machine learning algorithms indirectly, limiting the
minimum prefix size corresponds directly to network generality.
![]() Memory: A natural means to bound memory.
Because the tree structure provides longest-match lookups, the
algorithm can sacrifice accuracy for lower memory utilization by
bounding tree depth or width.
Memory: A natural means to bound memory.
Because the tree structure provides longest-match lookups, the
algorithm can sacrifice accuracy for lower memory utilization by
bounding tree depth or width.
![]() Change Detection: Allows for direct analysis on tree
nodes. Analysis on these individual nodes can
determine if part of the underlying network has changed.
Change Detection: Allows for direct analysis on tree
nodes. Analysis on these individual nodes can
determine if part of the underlying network has changed.
![]() On-Line Learning: When relearning stale information,
the longest match nature of the tree implies that once
information is discarded, in-progress predictions will use the next
available longest match which is likely to be more accurate than an
unguided prediction.
On-Line Learning: When relearning stale information,
the longest match nature of the tree implies that once
information is discarded, in-progress predictions will use the next
available longest match which is likely to be more accurate than an
unguided prediction.
![]() Active Learning: Real training data is likely to
produce an unbalanced tree, naturally suggesting active learning.
While guided learning decouples training from
testing, sparse or poorly performing portions of the tree
are easy to identify.
Active Learning: Real training data is likely to
produce an unbalanced tree, naturally suggesting active learning.
While guided learning decouples training from
testing, sparse or poorly performing portions of the tree
are easy to identify.
A radix, or Patricia [10], tree is a compressed tree that stores strings. Unlike normal trees, radix tree edges may be labeled with multiple characters thereby providing an efficient data structure for storing strings that share common prefixes.
Radix trees support lookup, insert, delete and find predecessor
operations in ![]() time where
time where ![]() is the maximum length of all
strings in the set. By using a binary alphabet, strings of
is the maximum length of all
strings in the set. By using a binary alphabet, strings of ![]() bits and nexthops as values, radix trees support IP routing table
longest match lookup, an approach suggested by [13] and
others. We adopt radix trees to store our algorithm's inferred
structure model and provide predictions.
bits and nexthops as values, radix trees support IP routing table
longest match lookup, an approach suggested by [13] and
others. We adopt radix trees to store our algorithm's inferred
structure model and provide predictions.
Student's t-test [6] is a popular test to determine the statistical significance in the difference between two sample means. We use the t-test in our algorithm to evaluate potential partitions of the address space at different split granularity. The t-test is useful in many practical situations where the population variance is unknown and the sample size too small to estimate the population variance.
Note that by Eq. 1, the number of addresses within any
prefix (![]() ) is always a power of two. Additionally, a prefix
implies a contiguous group of addresses under common administration.
A naïve algorithm may assume that two contiguous (
) is always a power of two. Additionally, a prefix
implies a contiguous group of addresses under common administration.
A naïve algorithm may assume that two contiguous (![]() )
addresses,
)
addresses,
![]() and
and
![]() , are under common
control. However, by taking prefixes and address allocation into
account, an educated observer notices that:
, are under common
control. However, by taking prefixes and address allocation into
account, an educated observer notices that: ![]() (18.255.255.255) and
(18.255.255.255) and
![]() (19.0.0.0) can only be under common control if they belong to
the large aggregate
(19.0.0.0) can only be under common control if they belong to
the large aggregate
![]() . A third address
. A third address
![]() , separated by
, separated by
![]() , is further from
, is further from
![]() , but more likely to belong with
, but more likely to belong with ![]() than is
than is ![]() .
.
We incorporate this domain-specific knowledge in our algorithm by inducing splits on power of two boundaries and ensuring maximal prefix splits.
Assume the t-test procedure identifies a ``good'' partitioning. The partition defines two chunks (not necessarily contiguous), each of which contains data points with statistically different characteristics. We ensure that each chunk is valid within the constraints in which networks are allocated.
If a chunk of address space is not valid for a particular partition, it must be split. We therefore introduce the notion of maximal valid prefixes to ensure generality.
Consider the prefix
![]() in Figure 2. Say
the algorithm determines that the first quarter of this space (shaded)
has a property statistically different from the rest (unshaded). The
unshaded three-quarters of addresses from
in Figure 2. Say
the algorithm determines that the first quarter of this space (shaded)
has a property statistically different from the rest (unshaded). The
unshaded three-quarters of addresses from
![]() to
to
![]() is not valid. The space could be divided into three
equally sized
is not valid. The space could be divided into three
equally sized ![]() valid prefixes. However, this naïve choice
is wrong; in actuality the prefix is split into three different
autonomous systems (AS). The IP address registries list
valid prefixes. However, this naïve choice
is wrong; in actuality the prefix is split into three different
autonomous systems (AS). The IP address registries list
![]() as being in Sacramento, CA,
as being in Sacramento, CA,
![]() as
Atlanta, GA and
as
Atlanta, GA and
![]() in Oregon. Using maximally sized
prefixes captures the true hierarchy as well as possible given sparse
data.
in Oregon. Using maximally sized
prefixes captures the true hierarchy as well as possible given sparse
data.
We develop an algorithm to ensure maximal valid prefixes along with proofs of correctness in [3], but omit details here for clarity and space conservation. The intuition is to determine the largest power of two chunk that could potentially fit into the address space. If a valid starting position for that chunk exists, it recurses on the remaining sections. Otherwise, it divides the maximum chunk into two valid pieces. Table 1 gives three example divisions.
Using the radix tree data structure, t-test to evaluate potential
partitions and notion of maximal prefixes, we give the complete
algorithm. Our formulation is based on a divisive approach;
agglomerative techniques that build partitions up are a potential
subject for further work. Algorithm 1 takes a prefix
![]() along with the data samples for that prefix:
along with the data samples for that prefix:
![]() . The threshold defines a cutoff
for the t-test significance and is notably the only parameter.
. The threshold defines a cutoff
for the t-test significance and is notably the only parameter.
The algorithm computes the mean ![]() of the
of the ![]() input and adds
an entry to radix table
input and adds
an entry to radix table ![]() containing
containing ![]() pointing to
pointing to ![]() (lines
1-4). In lines 5-12, we create partitions
(lines
1-4). In lines 5-12, we create partitions ![]() at a granularity of
at a granularity of
![]() as described in Eq. 2. For each
as described in Eq. 2. For each ![]() ,
line 13 evaluates the t-test between points within and without the
partition. Thus, for
,
line 13 evaluates the t-test between points within and without the
partition. Thus, for ![]() , we divide
, we divide ![]() into eighths and evaluate
each partition against the remaining seven. We determine the lowest
t-test value
into eighths and evaluate
each partition against the remaining seven. We determine the lowest
t-test value ![]() corresponding to split
corresponding to split ![]() and
partition
and
partition ![]() .
.
If no partition produces a split with t-test less than a threshold, we
terminate that branch of splitting. Otherwise, lines 16-25 divide the
best partition into maximal valid prefixes
(§3.5), each of which is placed into the set
![]() . Finally, the algorithm recurses on each prefix in
. Finally, the algorithm recurses on each prefix in ![]() .
.
The output after training is a radix tree which defines clusters.
Subsequent predictions are made by performing longest prefix matching
on the tree. For example, Figure 3 shows the tree
structure produced by our clustering on input
![]() (
(
![]() ,
,
![]() ), (
), (
![]() ,
, ![]() ), (
), (![]() ,
, ![]() ),
(
),
(![]() ,
, ![]() ), (
), (![]() ,
, ![]() ), (
), (![]() ,
, ![]() ).
).
| 
| 
|
| a. |
b.
| c. Impulse triggered change detection |
An important feature of the algorithm is its ability to accommodate network dynamics. However, first the system must detect changes in a principled manner. Each node of the radix tree naturally represents a part of the network structure, e.g. Figure 3. Therefore, we may run traditional change point detection [2] methods on the prediction error of data points classified by a particular tree node. If the portion of the network associated with a node exhibits structural or dynamic changes, evidenced as a change in prediction error mean or variance respectively, we may associate a cost with retraining. For instance, pruning a node close to the root of the tree represents a large cost which must be balanced by the magnitude of predictions errors produced by that node.
When considering structural changes, we are concerned with a change in
the mean error resulting from the prediction process. Assume that
predictions produce errors from a Gaussian distribution
![]() . As we cannot assume, a priori, knowledge of how
the processes' parameters will change, we turn to the well-known
generalized likelihood ratio (GLR) test. The GLR test statistic,
. As we cannot assume, a priori, knowledge of how
the processes' parameters will change, we turn to the well-known
generalized likelihood ratio (GLR) test. The GLR test statistic,
![]() can be shown to detect a statistical change from
can be shown to detect a statistical change from ![]() (mean before
change). Unfortunately, GLR is typically used in a context where
(mean before
change). Unfortunately, GLR is typically used in a context where
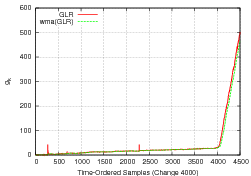
![]() is well-known, e.g. manufacturing processes. Figure
4(a) shows
is well-known, e.g. manufacturing processes. Figure
4(a) shows ![]() as a function of ordered prediction
errors produced from our algorithm on real Internet data. Beginning
at the 4000th prediction, we create a synthetic change by adding 50ms
to the mean of every data point (thereby ensuring a 50ms error for an
otherwise perfect prediction). We use a weighted moving average to
smooth the function. The change is clearly evident. Yet
as a function of ordered prediction
errors produced from our algorithm on real Internet data. Beginning
at the 4000th prediction, we create a synthetic change by adding 50ms
to the mean of every data point (thereby ensuring a 50ms error for an
otherwise perfect prediction). We use a weighted moving average to
smooth the function. The change is clearly evident. Yet ![]() drifts
even under no change since
drifts
even under no change since ![]() is estimated from training data
error which is necessarily less than the test error.
is estimated from training data
error which is necessarily less than the test error.
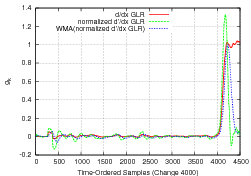
To contend with this GLR drift effect, we take the derivative of ![]() with respect to sample time to produce the step function in
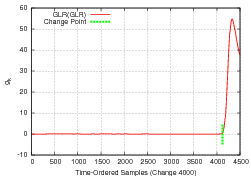
Figure 4(b). To impulse trigger a change, we
take the second derivative as depicted in Figure 4(c).
Additional details of our change inference procedure are given in
[3].
with respect to sample time to produce the step function in
Figure 4(b). To impulse trigger a change, we
take the second derivative as depicted in Figure 4(c).
Additional details of our change inference procedure are given in
[3].
We evaluate our clustering algorithm on both real and synthetic input data under several scenarios in [3]; this section summarizes select results from live Internet experiments.
Our live data consists of latency measurements to random Internet hosts (equivalent to the random pairs in §2.2). To reduce dependence on the choice of training set and ensure generality, all results are the average of five independent trials where the order of the data is randomly permuted.
Figure 5 depicts the mean prediction error and standard deviation as a function of training size for our IP clustering algorithm. With as few as 1000 training points, our regression yields an average error of less than 40ms with tight bounds - a surprisingly powerful result given the size of the input training data relative to the allocated Internet address space. Our error improves to approximately 24ms using more than 10,000 training samples to build the model.
To place these results in context, consider a fixed-size lookup table
as a baseline naïve algorithm. With a ![]() -entry table, each
training address
-entry table, each
training address ![]() updates the latency measure corresponding to
the
updates the latency measure corresponding to
the ![]() 'th row. Unfortunately, even a
'th row. Unfortunately, even a ![]() -entry table performs
5-10ms worse on average than our clustering scheme. More problematic
is this table requires more memory than is practical in applications
such as a router's fast forwarding path. In contrast, the tree data
structure requires
-entry table performs
5-10ms worse on average than our clustering scheme. More problematic
is this table requires more memory than is practical in applications
such as a router's fast forwarding path. In contrast, the tree data
structure requires ![]() 130kB of memory with 10,000 training points.
130kB of memory with 10,000 training points.
A natural extension of the lookup table is a ``nearest neighbor scheme:'' predict the latency corresponding to the numerically closest IP address in the training set. Again, this algorithm performs well, but is only within 5-7ms of the performance obtained by clustering and has a higher error variance. Further, such naïve algorithms do not afford many of the benefits in §3.1.
Finally, we consider performance under dynamic network conditions. To evaluate our algorithm's ability to handle a changing environment, we formulate the induced change point game of Figure 6. Within our real data set, we artificially create a mean change that simulates a routing event or change in the physical topology. We create this change only for data points that lie within a randomly selected prefix. The game is then to determine the algorithm's ability to detect the change for which we know the ground truth.

The shaded portion of the figure indicates the true change within the IPv4 address space while the unshaded portion represents the algorithm's prediction of where, and if, a change occurred. We take the fraction of overlap to indicate the false negatives, false positives and true positives with remaining space comprising the true negatives.
Figure 7 shows the performance of our change detection technique in relation to the size of the artificial change. For example, a network change of /2 represents one-quarter of the entire 32-bit IP address space. Again, for each network size we randomly permute our data set, artificially induce the change and measure detection performance. For reasonably large changes, the detection performs quite well, with the recall and precision falling off past changes smaller than /8. Accuracy is high across the range of changes, implying that relearning changed portions of the space is worthwhile.
Through manual investigation of the change detection results, we find that the limiting factor in detecting smaller changes is currently the sparsity of our data set. Further, as we select a completely random prefix, we may have no a priori basis for making a change decision. In realistic scenarios, the algorithm is likely to have existing data points within the region of a change. We conjecture that larger data sets, in effect modeling a more complete view of the network, will yield significantly improved results for small changes.
Our algorithm attempts to find appropriate partitions by using a sequential t-test. We have informally analyzed the stability of the algorithm with respect to the choice of optimal partition, but wish to apply a principled approach similar to random forests. In this way, we plan to form multiple radix trees using the training data sampled with replacement. We then may obtain predictions using a weighted combination of tree lookups for greater generality.
While we demonstrate the algorithm's ability to detect changed portions of the network, further work is needed in determining the tradeoff between pruning stale data and the cost of retraining. Properly balancing this tradeoff requires a better notion of utility and further understanding the time-scale of Internet changes. Our initial work on modeling network dynamics by inducing increased variability shows promise in detecting short-term congestion events. Additional work is needed to analyze the time-scale over which such variance change detection methods are viable.
Thus far, we examine synthetic dynamics on real data such that we are able to verify our algorithm's performance against a ground truth. In the future, we wish to also infer real Internet changes and dynamics on a continuously sampled data set. Finally, our algorithm suggests at many interesting methods of performing active learning, for instance by examining poorly performing or sparse portions of the tree, which we plan to investigate going forward.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -no_navigation paper.tex
The translation was initiated by Rob Beverly on 2008-11-21