
The Windows Error Reporting system is a source of telemetry on user failures. When a process crashes or hangs and the user agrees to report the error, an error handler uploads a small chunk of metadata describing the crash. These reports are then placed into one of a large number of different failures, the most frequent of which are assigned to developers for review.
A common problem is duplication among these reports. Two reports can share the same root cause but be different in an insignificant way that causes them to be treated as separate failures. This can lead to duplication of effort when bugs are assigned round-robin to developers. It can also lead to misprioritization since the failure frequencies do not reflect the frequencies of the underlying issues.
Our paper proposes a similar-failure search engine to help rectify this. Given a failure, the goal of the engine is to find similar failures across a large global set. The primary use case is to allow a developer to check if a substantially similar failure was already resolved. A secondary use case is to provide diagnostic aid. For instance, consider a single bug that has led to a multitude of reports that are different, but share common attributes. Examining similar reports can highlight these attributes, providing clues about the underlying failure.
The search engine can draw on a variety of metadata available in the failure reports. Among other authors who have investigated user telemetry (see Brodie et al. (2005b), Brodie et al. (2005a) and Modani et al. (2007)), the offending callstack is the most popular source of identifying information about the failure. A popular approach is to treat the callstack as a string and apply string-matching techniques. This is employed by Brodie et al. (2005a) and Modani et al. (2007), who examine several heuristics for string matching, such as alignment, subsequences, prefix matching and edit distance. These string similarity measures are found to correlate highly with failure similarity.
Our work is novel in three respects. Foremost, rather than relying exclusively on ad-hoc heuristics, we employ machine learning to weight several heuristics in a tuned similarity measure. Second, we introduce new granularity in the callstack edit distance measure, allowing it to assign different edit penalties based on the properties of callstack frames, with these penalties learned from the data. Third, our similarity model is general enough to incorporate non-callstack features such as the process name, crash type and exception code of the failure.
The driver of our failure search engine is a similarity classifier, which provides a probabilistic similarity metric for failure pairs. To make our classifier mimic the developer's sense of ``similarity,'' we take labels from bug resolution records in which developers sometimes mark failures as duplicates. Our data are discussed in Section 2. Our similarity classifier model, its features and optimization are presented in Section 3, along with details on how to employ the classifier in a global similar-failure search engine. Section 4 presents our fitted models and compares their performance.
Our data are failure reports to the Windows Error Reporting system. Each failure has a set of descriptive attributes collected from the client, which are described in Section 2.1. To learn a similarity classifier, we need a training set comprised of labeled examples of failure pairs. Our approach, described in Section 2.2, employs duplicate failure designations made by developers in bug resolution reports.
Our global data set contains over one million failures collected over a 90-day period beginning April 1, 2008. In each report, a client-side process gathers the following metadata about the failure:
We shall frequently discuss frame groups: consecutive groups of frames in a callstack with the same module. In Table 1, there are five frame groups: one each for the frames associated with modules A3DHF8Q, user32 and ntdll, and two for kernel32.
To learn a similarity classifier, each observation in our training set must be a pair of failures tagged as either similar or dissimilar. We extract similar-pair examples from 327 bug resolution reports in which a developer marked one failure as a duplicate of another.
Obtaining examples of dissimilarity is less straightforward since
developers do not explicitly label failure pairs as
different. Instead, we construct pseudo-labelled data from
failure pairs that are examined but not resolved as
duplicates. One complication is that pairs of non-duplicates are not
guaranteed to be dissimilar. For instance, a developer may mark
several similar failures as unreproducible rather than marking them as
duplicates of each other. However, a developer who has already marked
several duplicates of a parent failure ![]() is likely to continue the
practice. Later failures that he does not mark as duplicates are, with
reasonable confidence, dissimilar from
is likely to continue the
practice. Later failures that he does not mark as duplicates are, with
reasonable confidence, dissimilar from ![]() .
.
Our entire strategy is diagrammed in Figure 1. Consider Developer X's resolution records. We first build a set of similar pairs using his duplicate resolutions. We next build a set of dissimilar pairs by combining his duplicates with his non-duplicates. Both sets can be large, so we pull one pair at random from each set. We thus obtain two rows for our training set, one for the similar pair and one for a dissimilar pair. This provides a total of 327 similar pairs and 327 dissimilar pairs in our training set.
![\includegraphics[width=0.7\linewidth]{LabelExtraction.eps}](img2.png) |
This section describes our failure similarity classifier. Section 3.1 introduces its features, and Section 3.2 presents the logistic probability model we employ for classification. We use maximum likelihood to estimate the parameters; our two-stage optimization scheme is discussed in Section 3.3. Finally, Section 3.4 describes how to deploy the fitted classifier in a fast global failure search engine.
To fit our training set, features must be defined over pairs of failures rather than single failures. We aim to construct one feature from each attribute, quantifying how a pair differs in that attribute. Our complete set of features is summarized in Table 2. The foremost is an edit distance measure of callstack similarity, discussed in Section 3.1.1. The other three are binary equivalence indicators, discussed in Section 3.1.2 for the categorical attributes.
| ||||||||||||||||||||||||
In tracking down failures related to a bug, developers often focus on a set of callstack frames that illuminate the bug. In general, the more frames two callstacks share, the more likely the parent failures are to be similar. We seek to incorporate this sense of similarity into our model.
Since a callstack is comprised of a sequence of frames, a natural measure of callstack similarity is Levenshtein edit distance, which measures similarity of two strings by the minimum number of fundamental edits - letter insertions, deletions or substitutions - required to transform one into the other (Levenshtein (1966)). It is typically also normalized by the maximum of the two strings' length (e.g., Marzal and Vidal (1993)) so that it falls between 0 and 1. The simplest way to adapt this for callstacks is to treat each unique combination of module, function and offset as a distinct letter. Each callstack is a ``string'' made up of such ``letters,'' allowing pairs of callstacks to be compared with Levenshtein distance. As shown in Figure 2, low callstack edit distance is highly predictive of failure similarity. Other authors, such as Modani et al. (2007) and Brodie et al. (2005a), have noted similar trends.
We next employ two adaptations of edit distance to improve its discriminative ability for callstacks. First, while standard Levenshtein distance equally penalizes the three fundamental edits, we seek to learn these penalties from the data. Ristad and Yianilos (1998) achieve this in the string comparison domain, learning the penalties based on a set of paired strings with labels. Our approach is similar, learning callstack edit penalties using failure pair labels.
Second, we introduce new fundamental edits to capture frame-level callstack differences. For instance, perhaps inserting a new frame group should be penalized more than inserting a new frame into an existing frame group. To capture this, we introduce the seven edits listed in Table 3. We penalize two types of insertions, those that begin a new frame group and those that add to an existing frame group. Likewise, we penalize deletions that close out a frame group separately from those that leave it in place. We also penalize substitutions separately based on the first point of difference between the frames at hand - the module, function or offset.
|
Computing edit distance with specialized penalty parameters involves a
straightforward parameterization of the edit costs in the canonical
dynamic programming solution. Because some callstacks are up to 1,000
frames, we implemented Gusfield (1997)'s method, which uses
![]() memory, where
memory, where ![]() and
and ![]() are the callstack sizes.
are the callstack sizes.
We next consider the three categorical attributes: failure type (crash, hang or deadlock), process name (one of 57 string values), exception code (one of six numeric values). We define one feature for each of these attributes, a binary indicator representing whether the failure pair in question shares the same value. For instance, a pair of failures both having process name ``wmplayer.exe'' would receive a 1 in the ``equivalence of process names'' feature. We construct three such equivalence features. The plots in Figure 3 show how these features influence failure similarity. For all three, attribute equivalence leads to a significantly greater probability of similarity.
One might note that our binary equivalence features do not take into account the individual values taken on by the failure pair. For instance, a pair of failures with process names ``wmplayer.exe'' and ``WinMail.exe'' is treated the same as a pair with ``svchost.exe'' and ``Zune.exe.'' This assumption simplifies modeling because it limits the combinatorial explosion of features over attribute values. It simplifies prediction because it does not require a strategy for dealing with previously unseen values, which is a major benefit because all three attributes have the Zipfian property that their cardinality forever grows as more failures are observed.
Our machine learning approach is statistical: we model the probability
that two failures are equal based on a parameterized combination of
features, and then apply maximum likelihood to estimate these
parameters. We define a linear logistic probability model
incorporating the four features in Table 2:
Here
![]() , the inverse logit function
also used in logistic regression. In this framework, the parameters
, the inverse logit function
also used in logistic regression. In this framework, the parameters
![]() linearly impact the similarity probability on the logit
scale. This is in contrast to the parameters
linearly impact the similarity probability on the logit
scale. This is in contrast to the parameters ![]() governing
the relative penalties of the fundamental edit types in Table
3, which impact similarity in a nonlinear
fashion.
governing
the relative penalties of the fundamental edit types in Table
3, which impact similarity in a nonlinear
fashion.
The most general model we fit incorporates all seven edit penalties and all four linear parameters. But to ensure our model's robustness, we also test whether a simpler model would suffice. To this end, we apply the deviance test (see McCullagh and Nelder (1989)) to a nested set of model specifications that progressively reduce the parameter space. We define four nested layers, shown below, so as to isolate each penalty's significance.
The model's log likelihood is
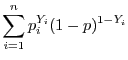 |
|||
Direct numerical optimization is expensive because each likelihood
evaluation requires recomputing all training edit distances for the
input ![]() . To mitigate this cost, observe from the form of
(1) that for fixed
. To mitigate this cost, observe from the form of
(1) that for fixed ![]() , the optimizing
, the optimizing
![]() are logistic regression estimates, which can be found
cheaply. This motivates a two-stage optimization routine based on
profile likelihood:
are logistic regression estimates, which can be found
cheaply. This motivates a two-stage optimization routine based on
profile likelihood:
The first step maximizes the profile likelihood over
![]() . This still requires numerical optimization, but with
far fewer function evaluations since the optimization is over
. This still requires numerical optimization, but with
far fewer function evaluations since the optimization is over
![]() alone. We recommend the simplex algorithm of
Nelder and Mead (1965) for two reasons. First, the edit distance function is
rough in
alone. We recommend the simplex algorithm of
Nelder and Mead (1965) for two reasons. First, the edit distance function is
rough in ![]() since changing penalties affects the minimum
edit path. This makes gradient-based optimizers unsuitable, whereas
Nelder-Mead does not employ the gradient. Second, we require a box
constraint to ensure that all penalties are positive and have unit
mean. This is easily accomplished in Nelder-Mead using boundary
penalties (see Lange (2001)). To evaluate
since changing penalties affects the minimum
edit path. This makes gradient-based optimizers unsuitable, whereas
Nelder-Mead does not employ the gradient. Second, we require a box
constraint to ensure that all penalties are positive and have unit
mean. This is easily accomplished in Nelder-Mead using boundary
penalties (see Lange (2001)). To evaluate
![]() , one can use any pre-packaged logistic
regression algorithm (e.g., iteratively reweighted least squares).
, one can use any pre-packaged logistic
regression algorithm (e.g., iteratively reweighted least squares).
Recall that the system's ultimate goal is to act as a search engine: to take a failure as input and return a list of similar failures from the global collection. Prediction runtime is dominated by the edit distance computation, which on a dual-core AMD64 machine takes an average 1 ms per callstack pair. Since repeating this for two million failures is prohibitively expensive, our system employs an initial search to limit the edit distance computation to failures that plausibly could be similar - defined as those whose callstacks share a sequence of three consecutive frames with the input failure. This is more rudimentary than other ``fast similarity search'' methods (see Gusfield (1997) for a summary or Bocek et al. (2008) for a recent example), which rely on terminating the edit distance computation after reaching a threshold distance. However, our search has the advantage of being easily implemented in a SQL database system, which can quickly query for callstacks sharing a sequence of frames. The number of common frames required can be tweaked so that the initial search returns a suitably small number of candidates; ours typically returns under 3,000. We then apply the fitted model to the remaining candidates, sorting them in the output by probability of similarity.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The estimated coefficients for all four models appear in Table
4. The full model is by far the best predictor, with the
gain from M1 to M2 strongly significant (
![]() ). There is
also a steep cascade of likelihoods through all the nested models,
meaning that all parameters are strongly significant. The biggest gain
comes from M3 to M2, when the substitution penalty is broken out by
module, function and offset. This suggests that this separation is the
key ingredient incorporated by our edit distance. Comparing the
relative values of the weights in the full models leads to several
supplementary conclusions:
). There is
also a steep cascade of likelihoods through all the nested models,
meaning that all parameters are strongly significant. The biggest gain
comes from M3 to M2, when the substitution penalty is broken out by
module, function and offset. This suggests that this separation is the
key ingredient incorporated by our edit distance. Comparing the
relative values of the weights in the full models leads to several
supplementary conclusions:
We compute precision-recall curves for our models using 10-fold cross-validation. For each of 10 equally-sized test sets, we re-estimate each model using all but the test set, applying them to produce held-out similarity probabilities for the test set. Repeating this over all 10 folds yields a held-out score for every pair from all four models.
We benchmark our methods against two simple heuristics suggested by Brodie et al. (2005a) and Modani et al. (2007):
The curves are overlaid in Figure 4. All models far outperform the baseline heuristics. Internally, they stack up as suggested by the log-likelihood, with Models 1 and 2 the clear winners. From Model 2 to Model 3, when the substitution penalties are stratified, is the biggest point of improvement. Models 3 and 4 show poorer precision for most levels of recall. Among their false positives are callstack pairs with similar module patterns, but slightly different function names and offsets. Most of these are Windows functions with similar outcomes but somewhat different names. This confirms that stratification of the substitution penalty is a key component of the model.
Recall is the primary metric of interest in our application because it governs the number of similar failures the search engine can provide for a given failure. Models 1 and 2 both are both able to identify about 80% of the similar failure pairs with greater than 95% precision, whereas Models 3 and 4 can only identify about half of similar failure pairs with this accuracy.
We have trained a similarity metric, a classifier that predicts the probability that two failure reports are ``similar'' under a developer's notion of the term. The model's key feature is callstack edit distance with tuned edit penalties based on callstack frames. The tuned edit distance primarily penalizes module differences between the two failures' callstacks. We have shown the model to perform with greater than 90% precision on a 50% baseline for broad levels of recall. Finally, we have outlined a strategy for performing a fast similarity search to scan a global collection of failure reports.