



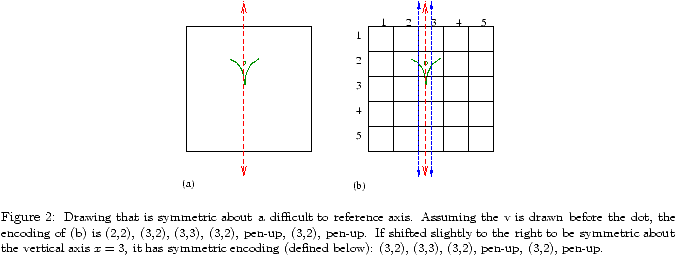
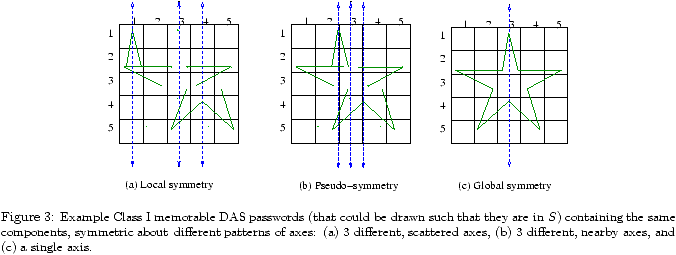
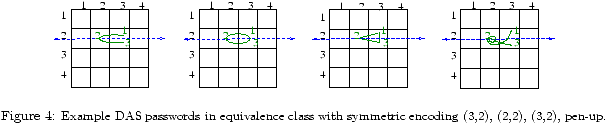
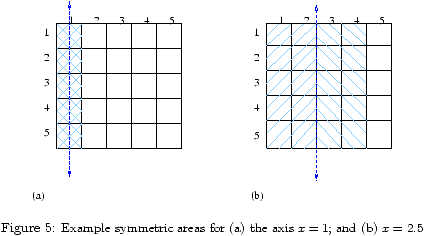
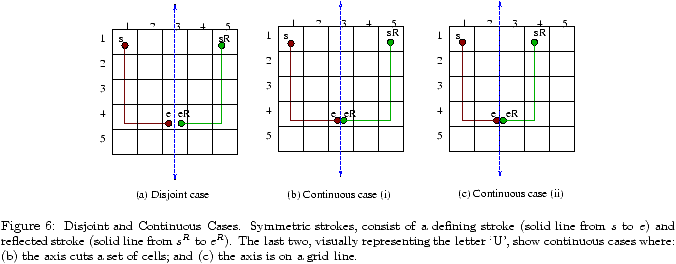
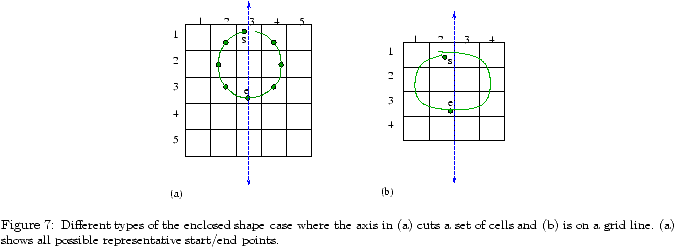
Lmax 1 2 3 4 5 6 7 8 9 10 Full DAS space 4.7 9.5 14.3 19.2 24.0 28.8 33.6 38.4 43.2 48.1 (i) S 4.7 9.5 14.3 19.1 23.9 28.7 33.6 38.4 43.2 48.0 (ii) SIa 3.3 7.7 11.6 15.7 19.8 23.8 27.9 31.9 36.0 40.0 (iii) SIb 3.3 6.9 10.5 14.1 17.7 21.2 24.8 28.4 32.0 35.6 Lmax 11 12 13 14 15 16 17 18 19 20 Full DAS space 52.9 57.7 62.5 67.3 72.2 77.0 81.8 86.6 91.4 96.2 (i) S 52.8 57.6 62.4 67.2 72.0 76.8 81.7 86.5 91.3 96.1 (ii) SIa 44.1 48.1 52.1 56.2 60.2 64.3 68.3 72.4 76.4 80.4 (iii) SIb 39.1 42.7 46.3 49.9 53.4 57.0 60.6 64.2 67.8 71.4
Table 1: Bit-size of graphical password space, for total length at most Lmax on a 5 × 5 grid.

The times provided in Table 2 highlight the implications of the graphical dictionary size. Assuming that we want an attacker to require an average of 10 years to exhaust these dictionaries with 1000 computers at 3.2GHz, the dictionary size must be approximately 263. Referring to Table 1, our Class Ib dictionary (global symmetry) is above this size when Lmax = 18. This implies that for this level of security (and a 5 × 5 grid), DAS users should choose passwords of length at least 18.
Dictionary Time to exhaust Time to exhaust (Lmax=12) (1 machine) (1000 machines) Full DAS Space 541.8 years 197.8 days S 505.6 years 184.5 days SIa 255 days 6.1 hours SIb 6 days 8.7 minutes
Table 2: Time to exhaust various dictionaries (3.2GHz machines, 5 × 5 grid).


